S 上のすべての点から A1,A2, … ,A8 のうち少なくとも2点が見えるための十分条件
l \geqq 2 \sqrt{3}r が十分条件なのは明らかな気がします。実際、 A1 から見下ろした図を描くと一目瞭然です(図5)。
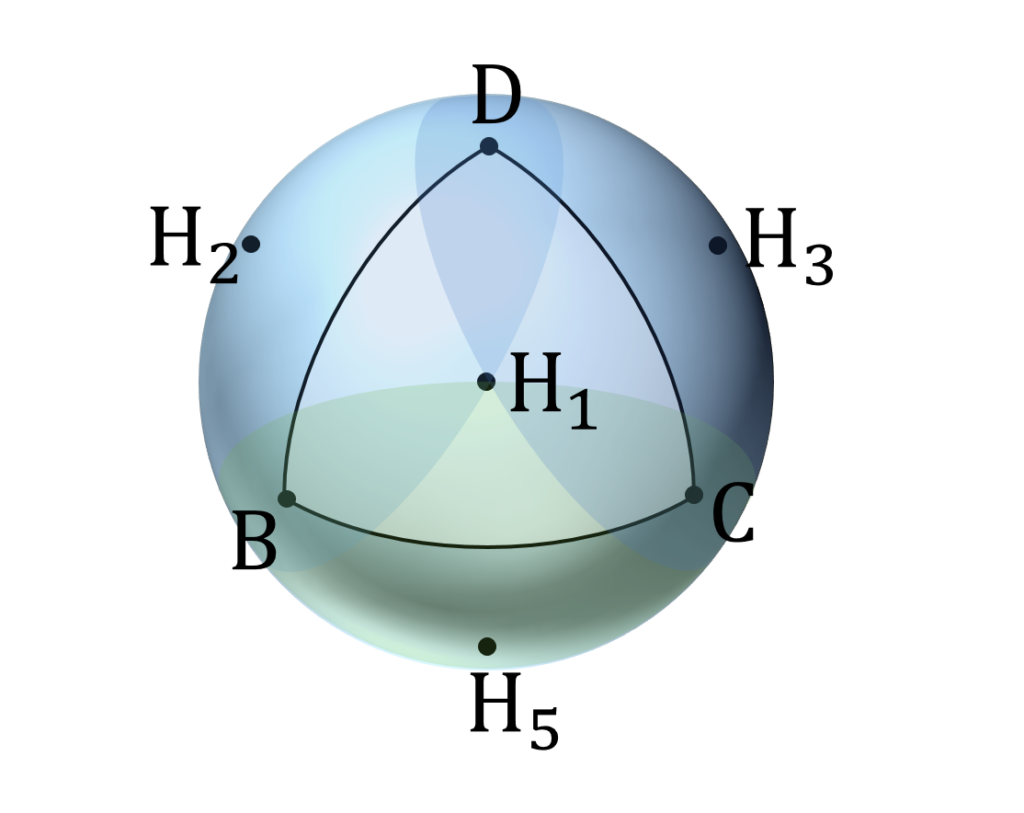
このように定性的には明らかですが、これだけだとモヤっとするのでもう少し定量的な証明を試みます。
S の第1象限上の点 P が頂点 A1 に隣接する A2,A3,A5 のどれかから監視できるということは、 OP と OA2,OA3,OA5 が成す角をそれぞれ φ2,φ3,φ5 とおくときに、 θ ≦ φ2 , θ ≦ φ3 , θ ≦ φ5 のいずれかが成り立つということです。すなわち
\cos \phi_2 \geqq \cos \theta_0 = \frac{2r}{ \sqrt{3}l} \\
\cos \phi_3 \geqq \cos \theta_0 = \frac{2r}{ \sqrt{3}l} \\
\cos \phi_5 \geqq \cos \theta_0 = \frac{2r}{ \sqrt{3}l} \\のいずれかが成り立てば P は A2,A3,A5 のどれかから監視できます。
l \geqq 2 \sqrt{3}r が成り立つとき、
\frac{2r}{ \sqrt{3}l} \leqq \frac{1}3なので、
\cos \phi_2 \geqq \frac{1}{ 3} \\
\cos \phi_3 \geqq \frac{1}{ 3} \\
\cos \phi_5 \geqq \frac{1}{ 3} \\のいずれかが成り立てば P は A2,A3,A5 のどれかから監視可能です。そこでこれが成り立つことを証明します。
ここで P がどれかの頂点の近傍領域(例えば図6)に存在するならその頂点が見える、という方向で進めようとすると、その近傍の定義など場合分けが面倒くさいので、図形や式の対象性が高いことを利用して場合分けなどせずに一気にサクッと解けないか、考えてみます。
図2の座標系に従って A2,A3,A5 の座標表示を
A_2( \frac{l}2, -\frac{l}2, \frac{l}2) \\
A_3( - \frac{l}2, \frac{l}2, \frac{l}2) \\
A_5( \frac{l}2, \frac{l}2, -\frac{l}2) \\とおきます。このとき
\begin{aligned}
\cos \phi_2 = & \frac{ \overrightarrow { ( \mathrm{OP}} , \overrightarrow { \mathrm{OA_2}} )} {||\overrightarrow{\mathrm{OP}}|| \cdot || \overrightarrow { \mathrm{OA_2}} ||} \\
= & \frac{ \frac{l}2 (x-y+z)}{r \cdot\frac{ \sqrt{3}}{2 } l} \\
= & \frac{1} { \sqrt{3} r}(x-y+z)
\end{aligned}\begin{aligned}
\cos \phi_3 = & \frac{ \overrightarrow { ( \mathrm{OP}} , \overrightarrow { \mathrm{OA_3}} )} {||\overrightarrow{\mathrm{OP}}|| \cdot || \overrightarrow { \mathrm{OA_3}} ||} \\
= & \frac{ \frac{l}2 (-x+y+z)}{r \cdot\frac{ \sqrt{3}}{2 } l} \\
= & \frac{1} { \sqrt{3} r}(-x+y+z)
\end{aligned}\begin{aligned}
\cos \phi_5 = & \frac{ \overrightarrow { ( \mathrm{OP}} , \overrightarrow { \mathrm{OA_5}} )} {||\overrightarrow{\mathrm{OP}}|| \cdot || \overrightarrow { \mathrm{OA_5}} ||} \\
= & \frac{ \frac{l}2 (x+y-z)}{r \cdot\frac{ \sqrt{3}}{2 } l} \\
= & \frac{1} { \sqrt{3} r}(x+y-z)
\end{aligned}ですが、この3式を x,y,z に関する連立方程式
\left \{
\begin{aligned}
x -y+z & = \sqrt{3} r \cos \phi_2 \\
-x +y+z & = \sqrt{3} r \cos \phi_3 \\
x +y-z & = \sqrt{3} r \cos \phi_5 \\
\end{aligned}
\right .に見立てて解き、その解を x,y,z に満たすべき条件に当てはめることで cosφ2, cosφ3 , cosφ5 に関する条件が得られないか探ってみます。
ところが、連立方程式を解くと
\left \{
\begin{aligned}
x & = \frac{ \sqrt{3} r }2( \cos \phi_2 +\cos \phi_5 ) \\
y & = \frac{ \sqrt{3} r }2( \cos \phi_3 +\cos \phi_5)\\
z & = \frac{ \sqrt{3} r }2( \cos \phi_2 +\cos \phi_3) \\
\end{aligned}
\right .なのでこれを x2 + y2 + z2 = r2 に代入すると、
\begin{aligned}
& \frac{ 3 r^2 }4( \cos \phi_2 +\cos \phi_5 )^2 \\
+& \frac{ 3 r^2 }4( \cos \phi_3 +\cos \phi_5 )^2 \\
+& \frac{ 3 r^2 }4( \cos \phi_2 +\cos \phi_3 )^2 \\
= & r^2
\end{aligned}
すなわち
\begin{aligned}
&( \cos \phi_2 +\cos \phi_5 )^2 \\
+& ( \cos \phi_3 +\cos \phi_5 )^2 \\
+& ( \cos \phi_2 +\cos \phi_3 )^2 \\
= & \frac{4}3
\end{aligned}
が成り立ちます。
ここで cosφ2 、 cosφ3 、 cosφ5 がすべて \displaystyle\frac{1}3 より小さいと仮定すると、0 ≦ x,y,z であったので
\begin{aligned}
& 0 \leqq \cos \phi_2 +\cos \phi_5 < \frac{2}3 \\
& 0 \leqq \cos \phi_3 +\cos \phi_5 < \frac{2}3\\
& 0 \leqq \cos \phi_2 +\cos \phi_3 < \frac{2}3\\
\end{aligned}
が成り立ち、よって
\begin{aligned}
&( \cos \phi_2 +\cos \phi_5 )^2 \\
+& ( \cos \phi_3 +\cos \phi_5 )^2 \\
+& ( \cos \phi_2 +\cos \phi_3 )^2 \\
< & \frac{4}9 + \frac{4}9 +\frac{4}9 = \frac{4}3
\end{aligned}
が成り立つはずですが、これは矛盾です。
したがって cosφ2, cosφ3 , cosφ5 の少なくとも1つは \displaystyle\frac{1}3 以上であるので、 P はA1 のほかに A2,A3,A5 のどれかからも監視可能です。
ゆえに、 l \geqq 2 \sqrt{3} r ならば S の第一象限が複数の頂点から監視可能です。したがって S 全体も複数の頂点から監視可能です。
以上、S 上のすべての点から A1,A2, … ,A8 のうち少なくとも2点が見えるための必要十分条件は、 l \geqq 2 \sqrt{3} r であることが証明できました。
解法のポイント
本問のような球面を扱う問題の場合、球面の中心原点として極座標的に角度で考えると、いろいろな条件をすっきり表現できることがあります。
一方、足し算や引き算の評価が必要な場合はデカルト座標のほうが便利です。本稿で示したように、必要に応じて使い分けてみてください。
小問2の十分条件をガチで証明しようとすると結構面倒くさいですが、本問のように証明すべき内容や式の対称性が強いときはこれををうまく利用するようにしましょう。