AP ≧ PM のときのMの存在領域(上から見た図)
図3を真上から見てみます。すなわち、各点の xy 平面への射影を、元の点と同じ記号であらわすとき、M は半径 PM の円周上にあるので、PM の長さ(すなわち M が存在する円周の半径)がAPより短いなら、 M の存在範囲は以下の図4のように、ドーナツ状となります。
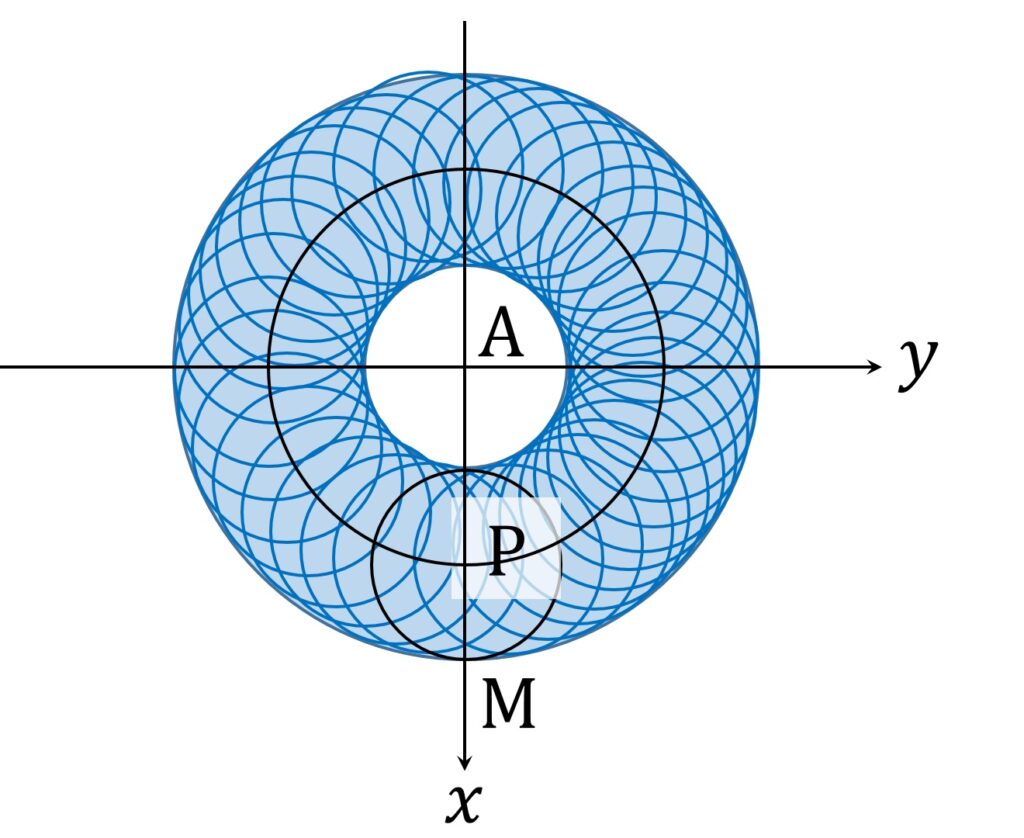
ドーナツ状領域の外側円周の半径は \mathrm{AP} + \mathrm{MP} =2-t + \frac{\sqrt{ 4- t^2 }}2 、内側円周の半径は \mathrm{AP} - \mathrm{MP} =2-t + \frac{\sqrt{ 4- t^2 }}2 なので、その面積は
\begin{aligned}
& \pi \left ( 2-t + \frac{\sqrt{ 4- t^2 }}2 \right )^2 \\
- & \pi \left ( 2-t - \frac{\sqrt{ 4- t^2 }}2 \right )^2 \\
= & 2\pi (2-t)\sqrt{ 4- t^2 }
\end{aligned}です。
AP ≦ PM のときのMの存在領域(上から見た図)
1 \leqq t \leqq 2 のとき、常に PM ≦ AP なら良いのですが、残念ながらそうではありません。
\begin{aligned}
\mathrm{PM} & = \frac{\sqrt{4-t^2}}{2} \\
\mathrm{AP} & = 2-t
\end{aligned}なので、 PM = AP のとき、
\frac{\sqrt{4-t^2}}{2} = 2-t
両辺を2乗して
\frac{4-t^2}{4} = (2-t)^2
両辺を4倍し、右辺を左辺に移項して
-12 + 16t -5t^2 = 0
左辺を因数分解して
-(t-2)(t-\frac{6}5) = 0すなわち、 \frac{6}5 \leqq t \leqq 2 のとき、PM ≧ AP です。このときの各点の配置は以下の通りです。
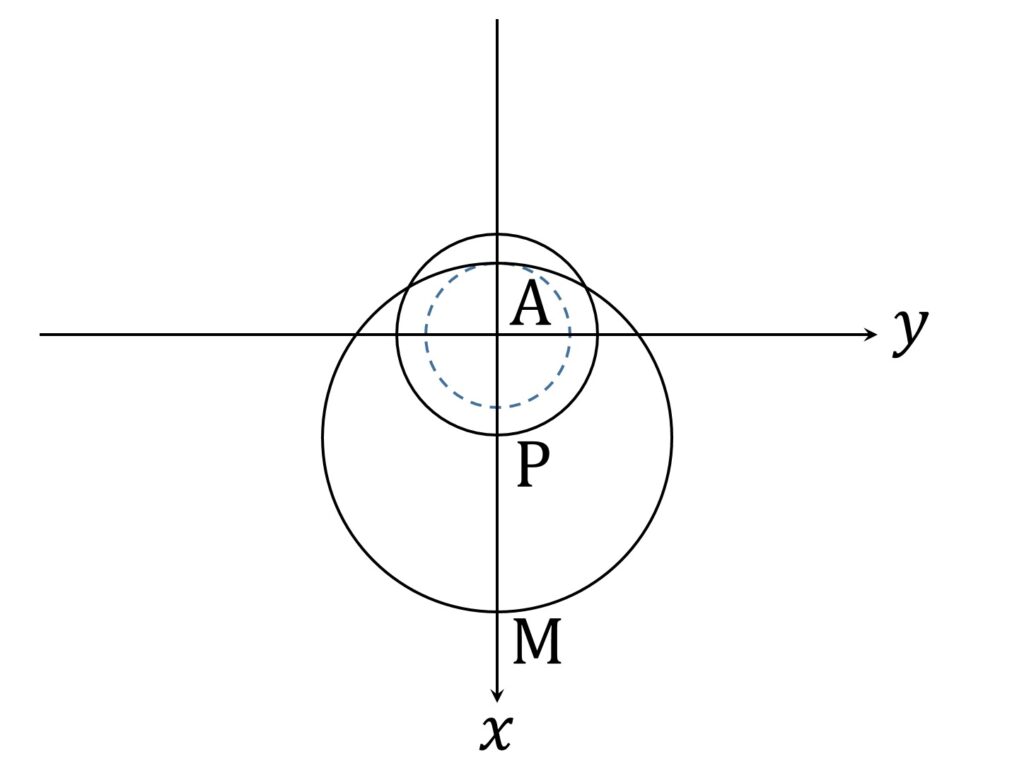
M が円周上を動くとき、AM の最小値は MP – AP = -2+t + \frac{\sqrt{ 4- t^2 }}2 です。 P がどこにあってもこの値は変わらないので、 M が存在する円周は常に、A を中心とする半径 MP – AP の円の外側にあります。よって、 M の存在領域は以下の図6の領域に含まれます。
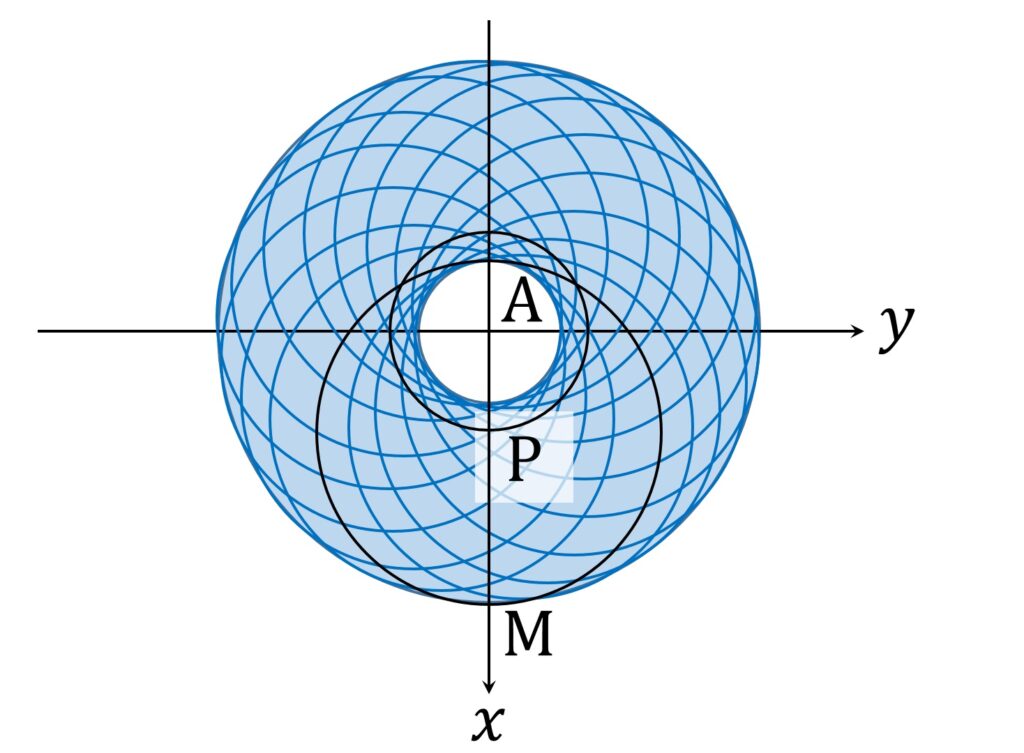
ドーナツ状領域の外側円周の半径は \mathrm{AP} + \mathrm{MP} =2-t + \frac{\sqrt{ 4- t^2 }}2 です。