十分性の証明
図6のエリアを以下の図7のように3つに分割します。
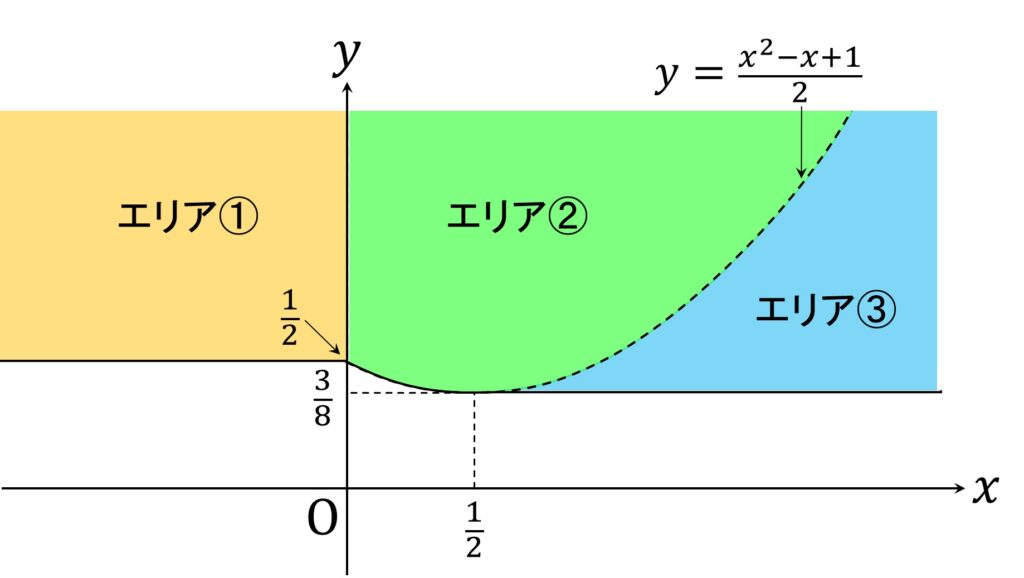
各エリアの定義は以下の通りです。
\begin{aligned}
& \text{エリア➀} : \\
&\{(x,y) \in \mathbb{R}^2 | x < 0 \text{かつ} \frac{1}2 \leqq y \} \\
& \text{エリア②} : \\
& \{(x,y) \in \mathbb{R}^2 | 0 \leqq x \text{かつ} \frac{x^2-x+1}2 \leqq y \} \\
& \text{エリア③} : \\
& \{(x,y) \in \mathbb{R}^2 | \frac{1}{2} < x \text{かつ} \frac{3}8 \leqq y < \frac{x^2-x+1}2 \} \\
\end{aligned}P ∈エリア➀のとき
まず P ∈エリア➀のとき、 a ≧ 0 を
\frac{a^2+a+1}2 = yの負でない解とします。 1 -2y ≦ 0 なので判別式が正になり、したがってその様な a は存在します。このとき a2+a+1=2y であり、かつ
\begin{aligned}
& x < 0 \leqq a\\
& 0 < \frac{1}2 \leqq y =\frac{a^2+a+1}2 < a^2+1
\end{aligned}なので
\begin{aligned}
d( \mathrm{O}, \mathrm{P} ) & = -x +y\\
d( \mathrm{P} ,\mathrm{Q}) &= -x- y +a^2+a+1 \\
&= -x +y
\end{aligned}であり、 d(O, P) = d(P, Q) が成り立ちます。
P ∈エリア②のとき
次に P ∈エリア②のとき、 a ≧ 0 を
\frac{a^2+a+1}2 =x+ yの負でない解とします。
\begin{aligned}
& 1 -2(x+y) \\
\leqq &1 -2x -(x^2-x+1) \\
= & -x^2-x \leqq 0
\end{aligned}なので判別式が正になり、したがってその様な a は存在します。このとき a2+a+1=2(x +y) であり、かつ
\begin{aligned}
a &= \frac{-1 + \sqrt{-3+8(x+y)}}2 \\
&\geqq \frac{-1 + \sqrt{-3+8(x+\frac{x^2-x+1}2 )}}2 \\
&=\frac{-1 + \sqrt{-3+4(x^2+x+1 )}}2 \\
&=\frac{-1 +2x+1}2 = x \geqq 0 \\
\end{aligned}かつ
\begin{aligned}
0< \frac{x^2-x+1}2 \leqq y & =\frac{a^2+a+1}2 -x \\
&< \frac{a^2+a+1}2 \\
&< a^2+1
\end{aligned}なので
\begin{aligned}
d( \mathrm{O}, \mathrm{P} ) & = x +y\\
d( \mathrm{P} ,\mathrm{Q}) &= -x- y +a^2+a+1 \\
&= x +y
\end{aligned}であり、 d(O, P) = d(P, Q) が成り立ちます。
P ∈エリア③のとき
最後に P ∈エリア③のとき、 a ≧ 0 を
\frac{a^2-a+1}2 = yの正の解とします。 1 -2y \leqq \displaystyle\frac{1}4 < 0 なので判別式が正になり、したがってその様な a は存在します。このとき a2–a+1=2y かつ
\begin{aligned}
a &= \frac{1 + \sqrt{-3+8y)}}2 \\
&\leqq \frac{1 + \sqrt{-3+8(\frac{x^2-x+1}2 )}}2 \\
&=\frac{1 + \sqrt{-3+4(x^2-x+1 )}}2 \\
&=\frac{1 +2x-1}2 = x \\
\end{aligned}かつ
\begin{aligned}
&0< \frac{3}8 \leqq y =\frac{a^2-a+1}2 < a^2+1
\end{aligned}なので
\begin{aligned}
d( \mathrm{O}, \mathrm{P} ) & = x +y\\
d( \mathrm{P} ,\mathrm{Q}) &= x- y +a^2-a+1 \\
&= x +y
\end{aligned}であり、 d(O, P) = d(P, Q) が成り立ちます。
以上、 P が図6のエリアに存在することであることが d(O, P) = d(P, Q) となるような a ≧ 0 が存在するための十分条件であることが示せました。