アステロイドとは
高校でちらりと出てくる、謎の曲線アステロイド。媒介変数表示は以下のとおりです。
x= \cos^3 t, y = \sin^3 t
入試でも余りフィーチャーされない、地味な存在ですが、ちょっと変わった性質を持っています。
アステロイドの意外な性質
xy 座標系において、 x軸上の点 A と y軸上の点 B が AB=1 を満たしながら動くとき、線分 AB の軌跡は何とアステロイドになります(図1)。
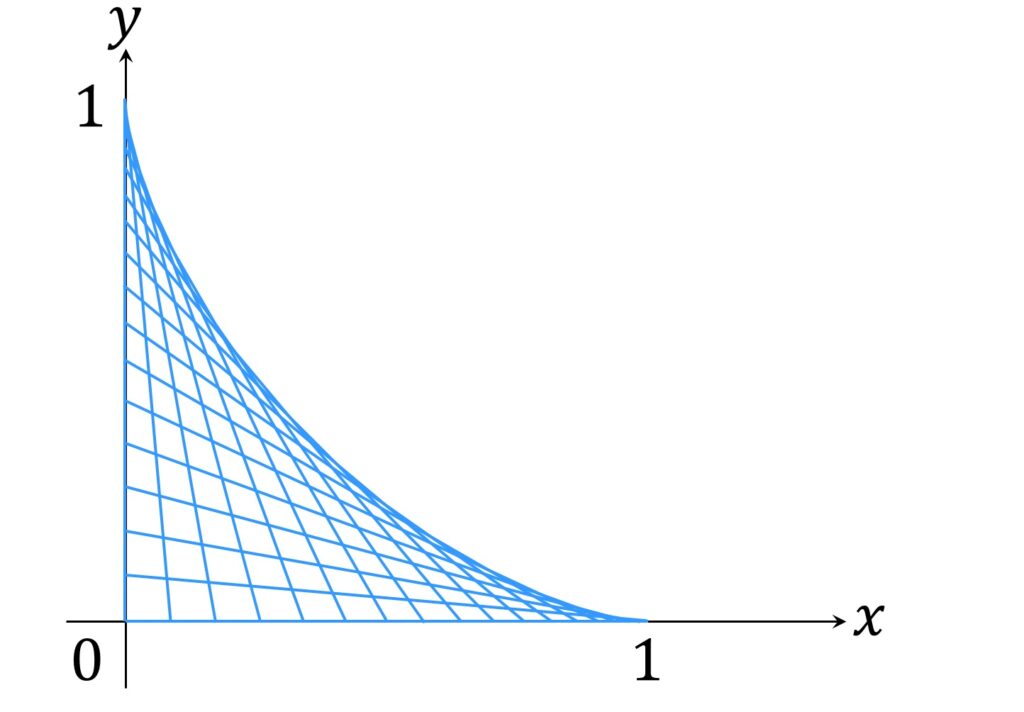
このことは教科書にも載っていませんし、ググってもなかなか見つけられませんでしたが、知っているとどこかで役に立つかもしれません。
簡単のため、第一象限で考えます。
0 ≦ α ≦ 1 に対し、直線 x = α と線分 AB の交点を P と置きます。 A が x軸上の非負部分を、 B がy軸上の非負部分を AB = 1 を満たしながら動くとき、 P の y 座標の最大値を f(α) と置きます。
すると、 y = f(x) はアステロイドです。
以下、このことを証明します。
証明
A,B の座標を
\begin{aligned}
A = & (x,0) \\
B = &( 0, \sqrt{1 - x^2}) \\
& ( 0 \leqq x \leqq 1)
\end{aligned}と定義します。
α ≦ x のとき、P の y 座標は x と α を使って以下のように表されます。
\frac{x- \alpha}{x} \sqrt{ 1- x^2}x < α のとき、直線 x = α と線分 AB は交点を持ちません。
α ≦ x のとき、x = cos θ と変数変換すると、
\frac{x- \alpha}{x} \sqrt{ 1- x^2} = \sin \theta - \alpha \tan \thetaです。そこで
g(\theta) = \sin \theta - \alpha \tan \theta
と置くと、
\begin{aligned}
g'(\theta) = & \cos \theta - \frac{\alpha} { \cos ^2 \theta} \\
= & \frac{\cos ^3 \theta - \alpha}{\cos ^2 \theta}
\end {aligned}
です。
ここで cos θ = α を満たす θ は 0 ≦ θ ≦ π/2 の範囲で1つだけ存在するので、これを θ1 と置くとき、
\cos ^3 \theta = \alpha
を満たす θ は 0 ≦ θ ≦ θ1 の範囲で1つだけ存在するので、これを θ0 とおくと、
| θ | 0 | … | θ0 | … | θ1 |
| g‘(θ) | + | 0 | – | ||
| g(θ) | 0 | ↗ | g(θ0) | ↘ | 0 |
となり、g(θ) は θ=θ0 のときに最大値
\begin{aligned}
g(\theta_0) = &\sin \theta_0 - \alpha \tan \theta_0 \\
= & \sin \theta_0 - \cos ^2 \theta_0 \sin \theta_0 \\
= & \sin^3 \theta_0
\end{aligned}をとります。
したがって f(α) = sin3 θ0 なので、 y = f(x) はアステロイドです。
本稿の内容は線分などの図形の軌跡に関する問題で役に立つかもしれないので、是非覚えておきましょう。

