交代和解法との関連
本問の解法としてポピュラーな交代和解法。筆者もその手法で解きましたが、交代和が不変量関数になるのは二面体群の性質によることを示します。
オセロ列 g \in \mathfrak{G} の構造を、図6のように定義します。
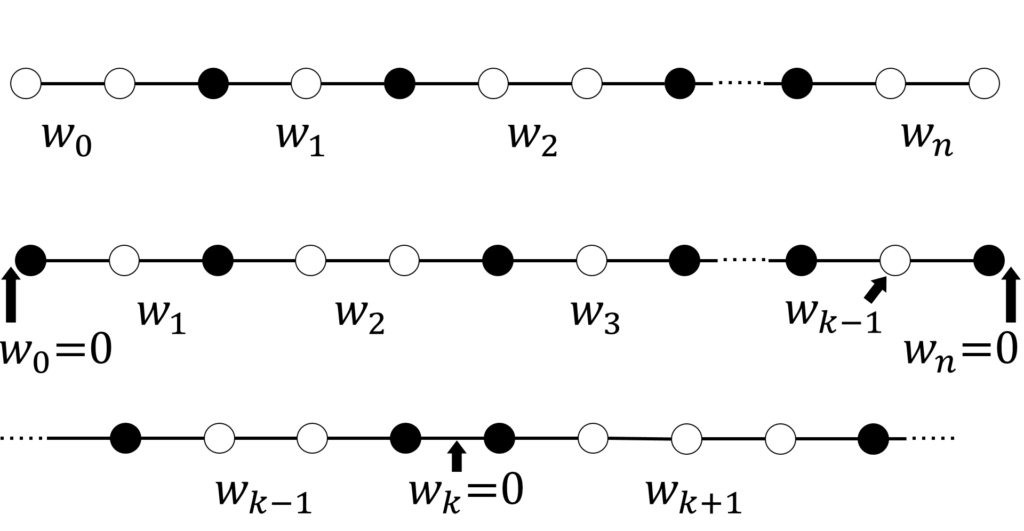
両端が白オセロであるオセロ列 g において、連続する白オセロを1つの群とし、その個数を左から順に w_k (k=0,1, \cdots ,n) と定義します。(図2上）。
g の左端が黒オセロの時は一番左に個数0の白オセロ群が存在していると解釈し、 w_0=0 とします。同様に g の右端が黒オセロの時は、一番右に個数0の白オセロ群があると解釈し、 w_n=0 とします(図2中）。
黒オセロは連続していても群にはまとめません。黒オセロと黒オセロの間に個数0の白オセロ群が存在していると解釈し、 w_k=0 とします(図2下）。
以上の準備の下に、拡張オセロ列 g \in EG を二面第群表記すると
f(g) = a^{w_0} ba^{w_1}b a^{w_2}\cdots a^{w_{n-1}} b a^{w_n}です。黒オセロ石は常に偶数個だったので、 n は必ず偶数です（白オセロ群に0から番号を振っていることに注意）。
ところで ba = a^2b なので、
ba^k = a^2ba^{k-1} =a^4ba^{k-2} =\cdots = a^{2k}bです。よって
ba^{w_{2m-1}}b a^{w_{2m}} = a^{2w_{2m-1}}bba^{w_{2m}} = a^{2w_{2m-1}+w_{2m}}が成り立ちます。したがって
\begin{aligned}
f(g) = & a^{w_0}a^{2w_1}a^{w_2} \cdots a^{w_{n-2}} a^{2w_{n-1}}a^{w_n} \\
= & a^{\sum\limits_{k \text{が偶数}} w_k +2\sum\limits_{k \text{が奇数}} w_k } =e
\end{aligned}が成り立つので、
\sum_{k \text{が偶数}} w_k +2\sum_{k \text{が奇数}} w_k \equiv 0 ( \mod 3)であり、 2 ≡ -1 (mod 3) なので
\sum_{k \text{が偶数}} w_k -\sum_{k \text{が奇数}} w_k \equiv 0 ( \mod 3)です。
以上、交代和が不変量関数になることは二面体群の性質から、特に難しい計算もなく必然的に導き出されます。
素の G における f(g) の挙動
拡張オセロ列 EG ではなく素の G において f(g) は不変量関数ではありませんが、面白い性質を持っています。以下ににそれを示します。
まず、オセロ列 g \in G の左側に操作１を施す場合を考えます。
g = 〇- g' であるとき f(g) = a\cdot f(g') です。よって
\begin{aligned}
f(\text{操作1}(g)) = & ab \cdot f(g') = baa \cdot f(g') \\
= &ba \cdot f(g)
\end{aligned}です。また g = ●- g' であるとき、 f(g) = b\cdot f(g') です。よって
\begin{aligned}
f(\text{操作1}(g)) = & aa \cdot f(g') = bab \cdot f(g') \\
= & ba \cdot f(g)
\end{aligned}です。したがって常に
f(\text{操作1}(g)) = ba \cdot f(g)が成り立ちます。
同様にして、オセロ列 g \in G の左側に操作１を施す場合、常に
f(\text{操作1}(g)) = f(g) \cdot abが成り立つことが示せます。
ここで左からの操作1を左操作1、右からの操作1を右操作1と表記することにします。
このとき、常に
f( \text{操作}2(g)) = f( g)なので、
\begin{aligned}
& f( \text{操作}2(\text{左操作}1(g)))\\
= & f(\text{左操作}1( g)) \\
= & ba\cdot f(g) \\
= & ba \cdot f(\text{操作}2(g)) \\
= & f( \text{左操作}1(\text{操作}2(g))) \\
\\
& f( \text{操作}2(\text{右操作}1(g))) \\
= & f(\text{右操作}1( g)) \\
= & f(g) \cdot ab \\
= & f(\text{操作}2(g)) \cdot ab \\
= & f( \text{左操作}1(\text{操作}2(g)))
\end{aligned}が成り立ち、したがって常に
\begin{aligned}
f( \text{操作}2(\text{操作}1(g))) = f( \text{操作}1(\text{操作}2(g)))
\end{aligned}が成り立ちます。
すなわち、二面体群に写像すると操作1と操作2は可換です。
よって任意のオセロ列 g \in G に対し
\begin{aligned}
& f(g) \\
= & f( \text{操作}2(\text{操作}2( \cdot \cdot (\text{操作}1(\text{操作}1 \cdot \cdot (g))) \cdot \cdot ) \\
= & f (\text{操作}1(\text{操作}1 \cdot \cdot (g))) \cdot \cdot )
\end{aligned}が成り立ちます。
ここで左操作1の施工回数を k 、右操作1の施工回数を l とおくとき、
\begin{aligned}
f(g) = (ba)^k a(ab)^l
\end{aligned}が成り立ちます。
\begin{aligned}
baba =(bab) a =a^3 =e \\
abab=a(bab) =a^3=e
\end{aligned}なので、 k,l の両方が偶数の時、
\begin{aligned}
f(g) =a
\end{aligned}です。また、 k,l の両方が奇数の時、
\begin{aligned}
f(g) =ba \cdot a \cdot ab = ba^3b = e
\end{aligned}です。
k が偶数、l が奇数の時、
\begin{aligned}
f(g) = a \cdot ab =ba
\end{aligned}です。
k が奇数、l が偶数の時、
\begin{aligned}
f(g) =ba \cdot a =ab
\end{aligned}です。
g \in G が白オセロ列ならば f(g) = e, f(g)=a,f(g)=a^2 のいずれかなので、上記の結果より g \in G が白オセロ列になるための必要条件は
- 長さが3で割って1余り、かつ右操作1の回数と左操作1の回数がともに偶数
- 長さが3で割れ、かつ操作1の回数と左操作1の回数がともに奇数
のいずれかです。すべての g \in G に対し f(g) \ne a^2 なので、ここからも長さ 3m+2 (m=0,1,2,…）の白オセロ列が生成されないことがわかります。拡張オセロ列を持ち出さなくても証明できました。
解法のポイント
問題文の主旨から本問が
a^3=b^2=e,bab = a^2
という性質を持つ何かに自然に写像できることに気が付けるかどうかがポイントです。行列になじみがあれば、本稿に示したような道筋で答えを出すこともできますが、学習指導要領に関する昨今の状況では厳しいかもしれません。
本問の解法はこれまで、オセロ石を単なるモノとしてとらえて個数だけを問題にし、操作1および操作2によって数がどう変動するかを調べることで答えを導き出すのが主流でしたが、本稿では操作2によるオセロ石の挙動が二面体群の性質に自然に同一視できることを示しました。本問の本質は、3次の二面体群であると言えるでしょう。