1997年東大 数学 後期 第1問 は正三角形パネルを順次塗りつぶしていったときに、塗りつぶされた数がどういう挙動をするかを回答する問題です。
問題文は以下のとおりで、東大2次試験からの引用です。
下の図のように,1 辺の長さが 1 の正三角形で,平面を分割する。

これらの 1 辺の長さが 1 の正三角形 1 つ 1 つを,単位正三角形とよぶことにする。
はじめに 1 個以上有限個の単位正三角形が塗りつぶされているとし,以下の操作を繰り返すことにより,次々に単位正三角形を塗りつぶしていく。
『1 回の操作ごとに,既に塗りつぶされている単位正三角形と少なくとも 1 つの辺を共有する単位正三角形を,すべて塗りつぶす』
次の問いに答えよ。
(1) はじめに塗りつぶされている単位正三角形が 1 つだけのとき,n 回目の操作が終わったときに塗りつぶされている単位正三角形の個数 a_n を求めよ。
(2) はじめに 2 個以上有限個の単位正三角形が塗りつぶされているとき, n 回目の操作が終わったときに塗りつぶされている単位正三角形の個数を b_n とおくと,極限 \lim\limits_{n\to\infty}\frac{a_n}{\,b_n\,} は,はじめの塗りつぶされ方がどのようであっても存在するか。極限が存在する場合については,その極限値を求めよ。存在しない場合があるならば,その例をあげよ。
エヴァのウィルスの回みたいな問題内容ですが、雰囲気が何となく、2004年 京大 後期 数学 第6問に似ています(本問のほうが年次が古いですが)。同じように極限を取ったりするので、似たような発想で解くことができるかもしれません。
それでは見ていきましょう。なお、本稿の内容は東大が発表したものではありません。
小問1の解法
まずは実際に数えて傾向をつかみましょう(図1)。a0 = 1 と置きます。
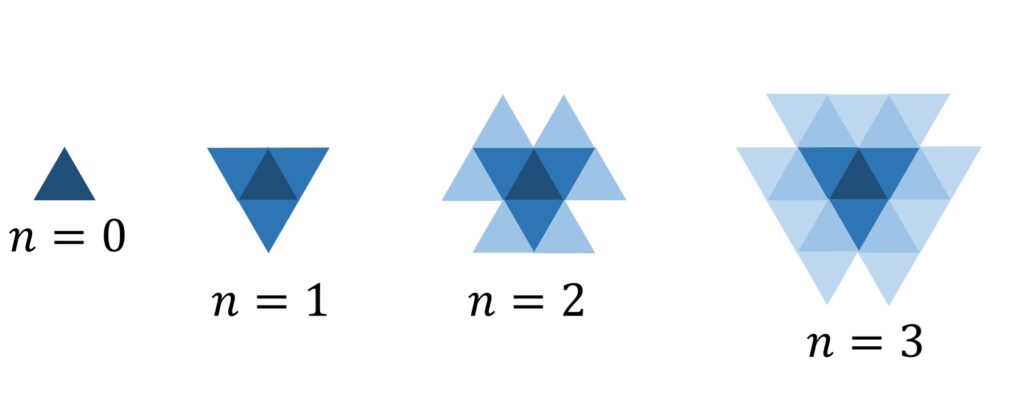
| n | an |
|---|---|
| 0 | 1 |
| 1 | 4 |
| 2 | 10 |
| 3 | 19 |
ちょっと何とも言えませんが、こういう時の常とう手段として隣接項の差分を取ってみると、
\begin{aligned}
a_1 - a_0 = 3 \\
a_2 -a_1 = 6 \\
a_3 -a_2 = 9
\end{aligned}です。
差分がいい感じに3の倍数になっているので、
a_{n} - a_{n-1} = 3nではないかと予想できます。
実はこの予想は正しいのですが、こいつの証明が難問です。 an の決まり方が図形の形に依存しているので、取りつく島がありません。
塗りつぶしを n 回繰り返したときにできる図形を An とします。 An に含まれる単位正三角形の数が an です。
An の外周の辺の数が次の塗りつぶしで増える単位正三角形の数ではないかと考えたくなりますが、外周がV字に切れ込んでいるところでは2辺に対し塗りつぶし正三角形が1つです。なので外周の辺の数で漸化式を立てることもできません。
ちょっと方針を立てられないので、とりあえず n を増やして図形の傾向を見ます(図2)。

だいぶ傾向が見えてきていて、図形の大まかな形状は6角形、ふちの形状が直線の場合とぎざぎざの場合が交互に現れます。
この気づきをヒントに、最初の正三角形の1辺から始まる塗りつぶし分に着目します(図3)。
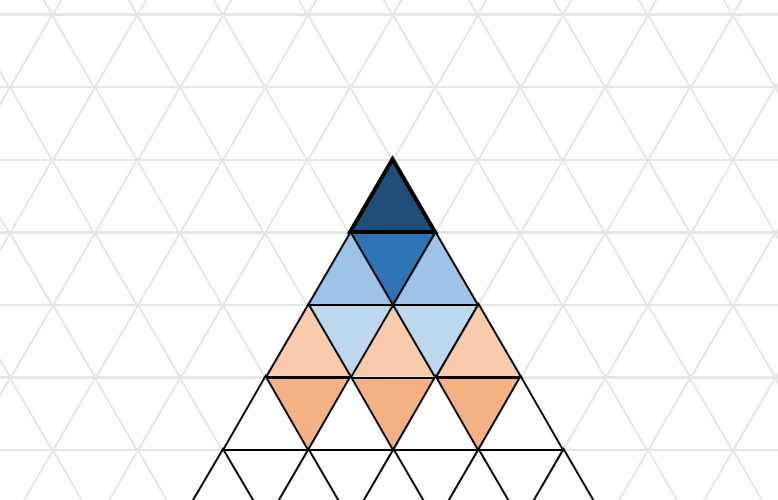
すると、境界が直線の時は次の三角形の数は前と同じ、境界がギザギザの時は次の三角形の数は前の三角形の数+1であることに気が付きます。
境界が直線になるのは n が奇数の時、ぎざぎざになるときは n が偶数の時です。よって、最初の正三角形の1辺から始まる塗りつぶしエリア内において、 n 回目の塗りつぶし個数を cn と置くとき、
\begin{aligned}
c_1 & = 1 \\
c_{n} &= \left \{
\begin{aligned}
& c_{n-1}(n \text{が奇数の時}) \\
& c_{n-1} +1(n \text{が偶数の時}) \\
\end{aligned}
\right .
\end{aligned}が成り立ちます。したがって n≧ 1 のとき
c_n =\left [\frac{n}2 \right ]+1が成り立ちます。
同様に、今度は最初の正三角形の頂点から始まる塗りつぶし分に着目します(図4)。

このエリアに塗りつぶしが現れるのは n ≧ 3 のときです。境界が直線になるのは n が偶数の時、ぎざぎざになるときは n が奇数の時なので、 n 回目の塗りつぶし個数を dn と置くとき、
\begin{aligned}
d_3 & = 1 \\
d_{n} &= \left \{
\begin{aligned}
& d_{n-1}(n \text{が偶数の時}) \\
& d_{n-1} +1(n \text{が奇数の時}) \\
\end{aligned}
\right .
\end{aligned}が成り立ちます。したがって n≧ 3 のとき
d_n =\left [\frac{n-1}2 \right ]が成り立ちます。
a_{n} - a_{n-1} = 3(c_{n} + d_{n})ですが、d1 = d2 = 0 とおくとき、
c_n + d_n = \left \{
\begin{aligned}
& \left [\frac{n}2 \right ]+1 (n =1,2)\\
& \left [\frac{n}2 \right ]+ \left [\frac{n-1}2 \right ]+1(n \geqq 3)\\
\end{aligned}
\right .が成り立ちます。
よって
c1 + d1 = 1
c2 + d2 = 2
です。
n ≧ 3 のとき、 n = 2m (m ≧ 2)ならば
\begin{aligned}
c_n +d_n & = \left [\frac{2m}2 \right ]+ \left [\frac{2m-1}2 \right ]+1 \\
&= m + m -1 +1= 2m = n
\end{aligned}n = 2m + 1 (m ≧ 1)ならば
\begin{aligned}
c_n +d_n & = \left [\frac{2m+1}2 \right ]+ \left [\frac{2m+1-1}2 \right ]+1 \\
&= m + m +1 = 2m+1 = n
\end{aligned}です。よってn ≧ 1 のとき
cn + dn = n
が成り立ちます。
したがってn ≧ 1 のとき
a_{n} - a_{n-1} = 3(c_{n} + d_{n}) = 3nが成り立つことが示せました。
あとは定石に従って an の一般項を求めるだけです。辺々足しこむことによって
a_{n} - a_0 = 3\sum_{k=1}^n k = \frac{3n(n+1)}2a1 = 1 なので、 n ≧ 1 のとき
a_{n} = \frac{3n(n+1)}2 + 1です。
小問2の解法
塗りつぶしを n 回繰り返したときにできる図形を Bn とします。 Bn に含まれる単位正三角形の数が bn です。
初期状態 B0 の形状がどんなものであっても、 n が十分に大きくなると正六角形に近づくのではないかと予想できます(図5)。
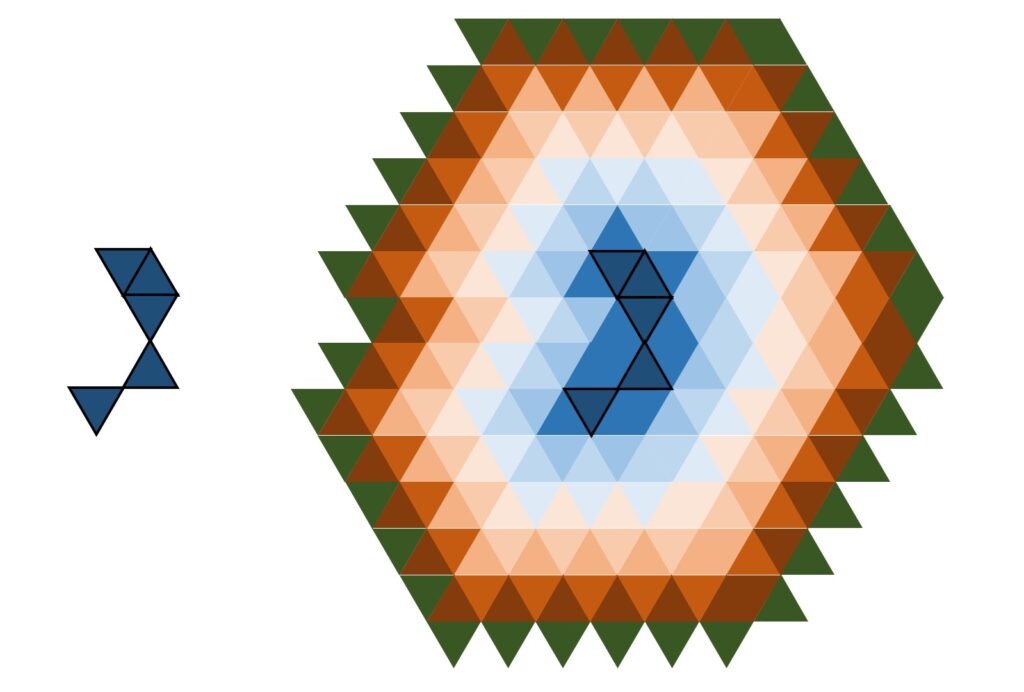
もしそうなら、an も bn も n2 のオーダーで増加するので、 \displaystyle\frac{a_n}{b_n} は何らかの値に収束しそうです。
さらに、 Bn は 少し大きめの An+N に常に包含されますが、その差は n が大きくなるにつれて無視できるようになります。したがって \lim\limits_{n \to \infty} \displaystyle\frac{a_n}{b_n} = 1 ではないかと予想できます。
そこでこれを証明します。
B0 の形がどのようであっても、自然数 N を十分大きくとれば B0 ⊂AN が成り立ちます。
このとき、すべての非負整数 n に対し、 Bn ⊂An+N が成り立つことが帰納的に示せます。
すなわち、 n=0 の時は明らかに成り立ちます。ある n に対して Bn ⊂An+N が成り立ったと仮定すると、 Bn+1 の各辺に隣接する単位正三角形の集合 Bn+1 \ Bnは An+1+N \ An+N に含まれるか、もとから An+N に含まれるかのいずれかで、どちらの場合でも An+1+N に含まれます。したがって Bn+1 ⊂An+1+N が成り立ちます。
以上、 Bn ⊂An+N が成り立つことが示せました。したがって
b_n \leqq a_{n+N}が成り立ちます。
同様にしてすべての自然数 n に対し、 An ⊂Bn が成り立ちます。したがって
a_n \leqq b_n
が成り立ちます。
よって
\frac{a_n}{a_{n+N}} \leqq \frac{a_n}{b_n} \leqq 1ですが
\begin{aligned}
\frac{a_n}{a_{n+N}} = & \frac{ \frac{3n(n+1) }{2}+1}{ \frac{3(n+N)(n+N+1)}{2} +1} \\
= & \frac{3(1 + \frac{1}n) + \frac{2}{n^2}}{3 (1 + \frac{N}{n})(1+ \frac{N+1}{n})+\frac{2}{n^2}}\\
\to & 1(n \to \infty)
\end{aligned}です。
ゆえにはじめの塗りつぶされ方がどのようであっても
\lim_{n \to \infty} \frac{a_n}{b_n} = 1です。
解法のポイント

小問1は求める数列 { an } が図形の形状で決まるので、とりあえず図を描いて傾向をつかみましょう。また、隣接項差分を取るのは常とう手段なので、必ず試してみましょう。
予想が立てられたとして、それを証明するのがまた一苦労ですが、理詰めだけで証明を思いつくのは結構しんどそうなので、やはり図を描いて証明方針を考えましょう。
小問2は Bn が何か円ぽいものに近づくのではないかと予想できれば、 An も Bn も同じ形状のものに近づくので B0 がどんな形でも少なくとも極限はありそうだ、と予測できます。
さらに、 Bn の「でこぼこ」が n が十分大きくなると無視できるようになるのでは、とイメージできれば本稿で示した解法にたどり着けるでしょう。この考え方は2004年 京大 後期 数学 第6問を解くときにも出てきていますが、図形全体が大きくなる時にでこぼこは相対的に無視できるという発想は使えますので覚えておきましょう。
