2025年京大 特色入試 数学 第4問 は三角関数の合成関数列という、難易度を上げるためだけに作り出されたとしか思えない謎の関数列に関する問題です。問題文は以下のとおりです。
自然数nに対して, 関数 f(x) を次で帰納的に定める.
\begin{aligned}
f_1 (x) = & \sin (x) \\
f_n (x) = & \sin ( f_{n-1}(x)) \text{ } ( n = 2,3,4, \cdots)
\end{aligned}また, Lを正の実数とし,
f_n (a) - \frac{a}L = 0を満たす実数aの個数を AL,n とする.このとき,以下の設問に答えよ.
(1) L≦1のとき, \lim\limits_{n \to \infty} A_{L,n } の値を求めよ.
(2) L>1のとき, \lim\limits_{n \to \infty} A_{L,n } の値を求めよ.
ただし,0以上の実数からなる数列 {an} が,任意の n に対してan+1 ≦ an を満たすとき, 数列 {an} が収束することを用いてもよい.
関数列 fn(x) が謎すぎて題意が頭に入ってきませんが、よく見ると AL,n というのは y = f_n(x) と y = g(x) = \displaystyle\frac{x}L の交点の数です。そう考えると小問1くらいは何とかなるかもしれません。それでは見ていきましょう。
2025年京大 特色入試 数学 第4問 小問1の解法
fn(x)のイメージを掴む
まず fn(x) がどういう代物なのか、イメージを掴みます。
明らかに fn-1(a) = fn-1(b) なら fn(a) = fn(b) なので、 fn(x + 2π) = fn(x) であることが帰納的に示せます。すなわち fn(x) は周期 2π の周期関数です。
また、明らかに fn(0) = fn(π) = 0 です。さらに、 sin 関数の基本的な性質 fn(x + π) = –fn(x) 、fn(x) = –fn(-x) 、 fn(x) = fn(π – x) なども成り立ちます。
したがって fn(x) はsin関数同様、
- 周期 2π の周期関数である
- 原点 O に関して対称である
- (π,0) に関して対称である
- 直線 x = π/2 に関して対称である
であることがわかりました。
また、 0 ≦ a < b ≦ π/2 なら 0 ≦ fn(a) < fn(b) ≦ 1 < π/2 であることが帰納的に示せます。したがって上で示した fn(x) の対称性より、sin関数同様
- 0 ≦ x ≦ π/2 で単調増加
- π/2 ≦ x ≦ 3π/2 で単調減少
- 3π/2 ≦ x ≦ 2π で単調増加
- 0 ≦ x ≦ π で fn(x) ≧ 0
- π ≦ x ≦ 2π で fn(x) ≦ 0
- x = π/2 で最大値をとり、 x = 3π/2 で最小値をとる
であることがわかりました。
さらに、 x > 0 のとき x > sin(x) なので、 0 < x < π の範囲で
fn-1(x) > sin(fn(x)) = fn(x) > 0
が成り立ちます。よって (π,0 ) における対称性により、π < x < 2π の範囲で
fn-1(x) < fn(x) < 0
が成り立ちます。
だいたいsin関数と同じような挙動で、 n が大きくなるほど絶対値が小さくなることがわかりました。
AL,n の値を求める
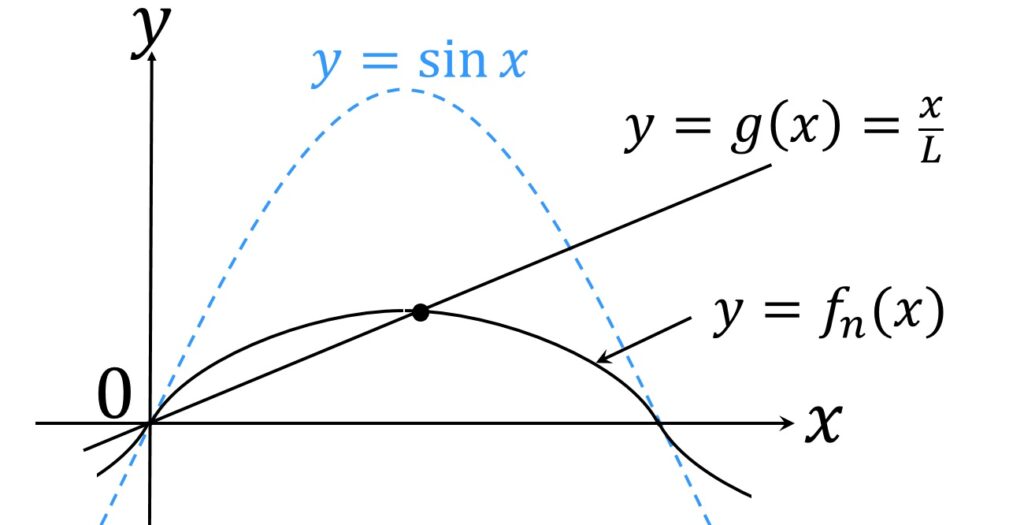
y = fn(x) および y = g(x) は原点 O を通るので、 AL,n ≧ 1 です。
0 < x の範囲で考えます。グラフの対称性により、この範囲での y = fn(x) とy = g(x) の交点の数の2倍に1を足したものが AL,n です。
L ≧ 1 なので直線 y = g(x) の傾きは 1 以上です。したがって x > 0 の範囲で y = g(x) と y = sin(x) は交点を持ちません。したがってy = fn(x) とy = g(x) も交点を持ちません。 2mπ < x < (2m+1)π ( m=0,1,…) のときは
fn(x) ≦ sin(x) < g(x)
であり、 (2m-1)π < x < 2mπ ( m=1,2,…) のときは
fn(x) ≦ 0 < g(x)
だからです。
ゆえにすべての自然数 n に対し AL,n = 1 であり、
\lim_{n \to \infty} A_{L,n} = 1です。
2025年京大 特色入試 数学 第4問 小問2の解法
小問1同様、 0 < x の範囲で考えます。
L > 1 なので直線 y = g(x) の傾きは 1 未満です。したがって x > 0 の範囲で y = g(x) と y = sin(x) は有限個の交点を持ちます。
そこでまず、 0 < x < π の範囲で、 y = fn(x) とy = g(x) の交点の数がいくつになるかを調べます。
まず、 fn‘(0) が n が大きくなるにつれてどうなるかを調べます。もしこれが0に収束するなら、y = fn(x) のグラフはおそらく上に凸(すなわち x = 0 における傾きが一番大きい)なので、グラフは n が大きくなるにつれて「つぶれて」いき、交点がないだろうと予想できます。
しかし f1‘(0) = cos(0) = 1なので、案外 fn‘(0) = 1 か、あるいは正の値で下から抑えられる気がします。
そこでこれを調べます。
fn‘(0) の値を求める
もしある自然数 n に対して fn‘(0) = 1 であったとすると、
\begin{aligned}
f_{n+1}'(x) = & \frac{d}{dx}\sin (f_{n}(x)) \\
= & \cos ( f_n(x)) \cdot f_n' (x)
\end{aligned}なので、 f‘n+1(0) = f‘n(0) = 1 です。したがってすべての自然数 n に対して fn‘(0) = 1 であることが帰納的に示せました。
思ったとおり fn‘(0) = 1 です。よって L > 1 のとき、原点における傾きは n がいくつであってもy = fn(x) のほうが y = g(x) より大きいので、原点の近傍では fn(x) > g(x) であるはずです。
一方 fn(π) = 0 ですが g(π) > 0 なので、y = fn(x) のグラフはsin(x) 同様きっと 0 < x < π の範囲で上に凸であろうから、 その範囲で y = fn(x) とy = g(x) の交点の数は1個だろうと予想できます(図1)。
そこでこれを証明します。
0 < x < π の範囲で交点の数が1個であることを証明する
hn(x) = fn(x) –g(x)
と置いて、これの増減表を書いてみます。ところが、
\begin{aligned}
h_n '(x) = & \cos (f_{n-1}(x)) \cdot f_{n-1}'(x) - \frac{1}L\\
\end{aligned}なので、 hn‘(x) の正負は簡単にはわかりそうにありません。そこでもう1回微分して L の項を消しましょう。
すると、
\begin{aligned}
h_n ''(x) = & - \sin (f_{n-1}(x)) \cdot (f_{n-1}'(x))^2 \\
& + \cos (f_{n-1}(x)) \cdot f_{n-1}''(x) \\
\end{aligned}ですが、0 < x < π の範囲で \sin (f_{n-1}(x)) \cdot (f_{n-1}'(x))^2 は常に負、 \cos (f_{n-1}(x)) は常に正です。
よって、 0 < x < π の範囲で f1’’(x) = -sin(x) < 0 なので、すべての自然数 n に対し fn”(x) < 0 であることが帰納的に示せます。思ったとおり、 fn(x) は0 < x < π の範囲で上に凸でした。
したがって fn‘(x) は 0 < x < π の範囲で単調減少関数です。
一方、
\begin{aligned}
h_n '(0) = & \cos (f_{n-1}(0)) \cdot f_{n-1}'(0) - \frac{1}L\\
= & 1 -\frac{1}L > 0 \\
h_n '(\pi) = & \cos (f_{n-1}(\pi)) \cdot f_{n-1}'(\pi) - \frac{1}L\\
= & \cos(0) \times( -f_{n-1}'(0)) - \frac{1}L\\
= & 1\times (-1) -\frac{1}L < 0 \\
\end{aligned}です。ここに fn-1‘(π) = –fn-1‘(0) = -1 は fn-1(x) = fn-1‘(π-x) であるところから導出できます。
よってfn‘(x) = 0 は 0 < x < π の範囲で解を一つだけ持ちます。それをαとおくとき、以下の増減表を書くことができます。
| x | 0 | … | α | … | π |
| hn‘(x) | 1- \frac{1}L | + | 0 | – | -1- \frac{1}L |
| hn(x) | 0 | \nearrow | hn(α) > 0 | \searrow | -\frac{\pi}L |
hn(α) > 0、 hn(π) < 0 であり、かつ α < x < π の範囲で hn(x) は単調減少なので、hn(x) = 0 はこの範囲で1つだけ解を持ちます。すなわち、0 < x < π の範囲で y = fn(x) とy = g(x) の交点の数は、 n の値に関わらず常に1つです。
π ≦ x ≦ 2π の範囲で fn(x) ≦ 0 なので、 y = fn(x) とy = g(x) の交点の数は当然0個です。したがって0 < x ≦ 2π の範囲で y = fn(x) とy = g(x) の交点の数は、 n の値に関わらず常に1つです。
2π < x の範囲で交点の数を求める
あとは 2π < x のとき y = fn(x) とy = g(x) の交点の数がどうなるかです。 0 < x < π の範囲で 0 < fn(x) < fn-1(x) なので fn(x) はなにかの値に収束します。よって fn(x) の対称性により、すべての x に対して fn(x) はなにかに収束します。
その「なにか」が何なのか明らかにできれば、2π < x の範囲で y = fn(x) とy = g(x) の交点の数がいくつなのか導出できそうですが、よく考えてみると収束値は0で、それはグラフを書いてみれば明らかです(図2)。
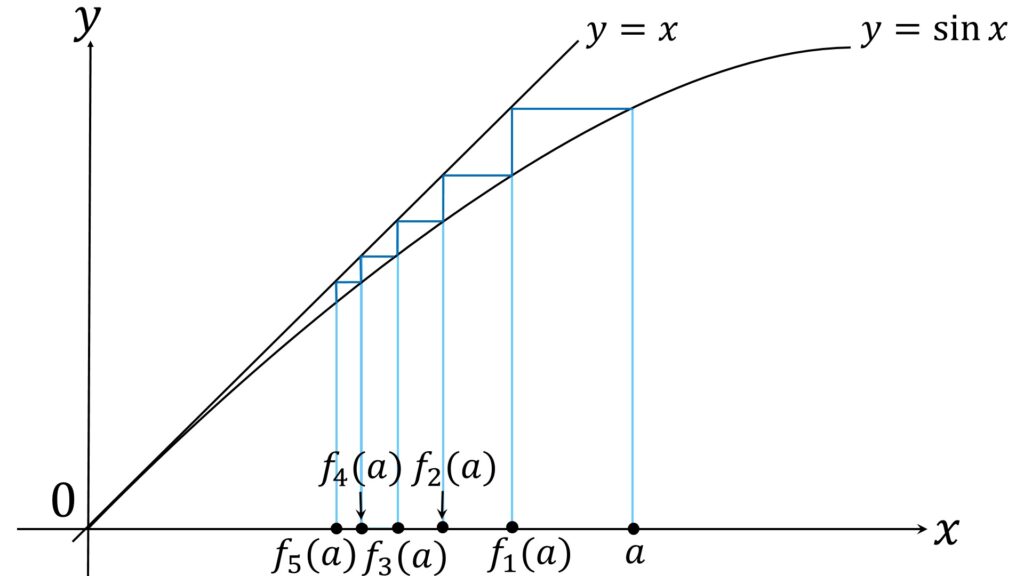
試験ではこれで通用すると思いますが、任意の x 対し \lim\limits_{n \to \infty} f_{n} (x) =a_x とおくと
\begin{aligned}
a_x = & \lim_{n \to \infty} f_n(x) \\
= & \lim_{n \to \infty} \sin (f_{n-1}(x) ) \\
= & \sin (\lim_{n \to \infty} f_{n-1}(x) ) \\
= & \sin ( a_x)
\end{aligned}であり、 y = sin(x) と y = x の交点は原点のみなので ax = 0 です。
特に fn(x) の最大値 f_n ( \frac{\pi}2 ) も0に収束するので、 L > 1 に対し n が十分に大きいとき、
f_n(\frac{\pi}2) < \frac{\pi}{2L}=g(\frac{\pi}2)であり、 y = fn(x) とy = g(x) の交点の数は 0 < x < π/2 の範囲で1個、 π/2 ≦ x の範囲ではずっと fn(x) < g(x) なので0個です。
ゆえに n が十分に大きいとき AL,n = 3 であり、
\lim_{n \to \infty} A_{L,n} = 3です。
解法のポイント

まず fn(x) のグラフの形がどういうものか、ある程度イメージを掴みましょう。 sin(x) と似ていることがわかれば、その先の方針が立てやすくなります。
小問2では fn‘(0) = 1 であることに気がつけるかどうかがキモですが、 fn(x) は sin(x) 同様上に凸だろうと予測していれば、 y = fn(x) のグラフが y =g(x) のグラフの「上側」に来るかどうかの判定が重要だと気がつけると思います。
微分を駆使して厳密に議論を進める前に、ざっくりイメージを掴む習慣をつけましょう。
