ツートン数珠均等分割問題 – 2006年京大 文系 数学 第5問

　京大の文系数学はかの有名な自分で得点を指定できる問題のように、情け容赦なく攻めた問題が多く出題されていますが、本問も相当キています。問題文は以下のとおりです。

　n，k は自然数で k ≦ n とする．穴のあいた 2k 個の白玉と 2n − 2k 個の黒玉にひもを通して輪を作る．このとき適当な 2 箇所でひもを切って n 個ずつの 2 組に分け，どちらの組も白玉 k 個，黒玉 n − k 個からなるようにできることを示せ.

　2種類の偶数個の数珠玉に糸を通して数珠を作るとき、数珠玉の並びがどのようなものであっても、数珠玉の種類と数が均等になるように数珠を2つに分割することができる、というのが問題文の主張です。

　言われてみればうまく分割できそうな気がしてきます。それでは見ていきましょう。

2006年京大 文系 数学 第5問 の解法

問題文の主旨をイメージする

　まずは何が言えれば問題文の内容が証明できたことになるのか、ざっくりイメージします。

　数珠の均等分割を考えるので、数珠玉を円周上に均等に並べたイメージを考えてみましょう。

　すると、数珠玉は偶数個あるので、各数珠玉は円の中心を挟んで反対側の数珠玉とペアにすることができます。数珠玉のペアはn個あり、数珠玉の組み合わせは白-白、黒-黒、白-黒の3種類です(図1)。

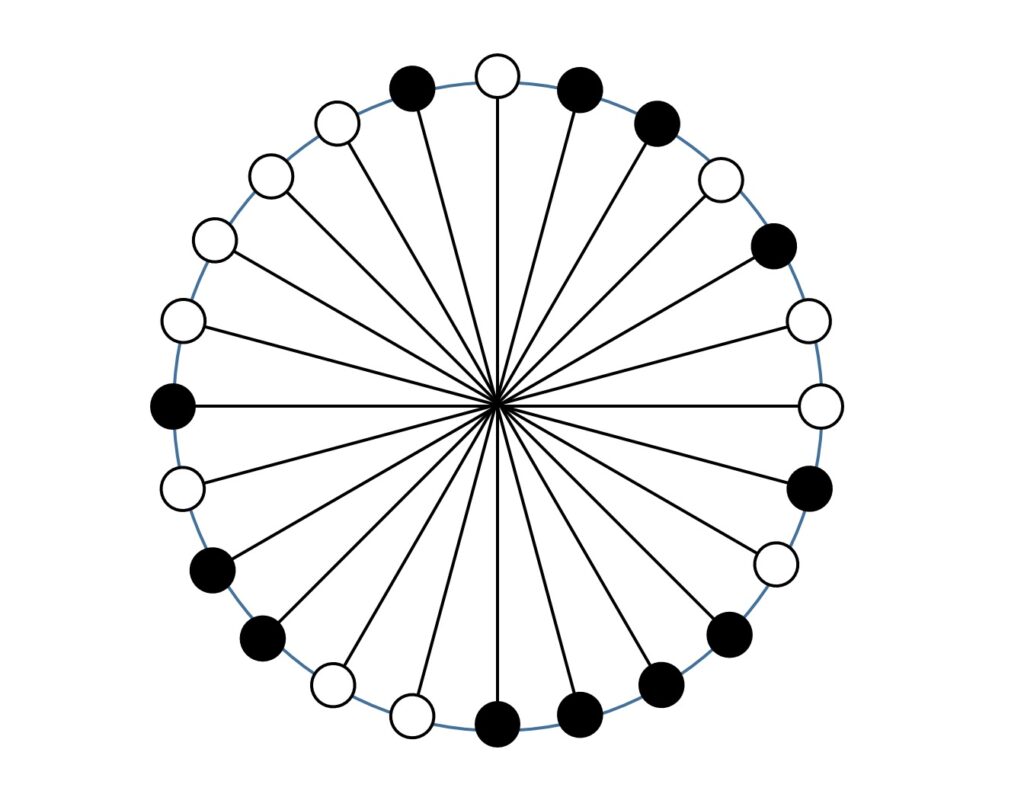
　ここまで考えたところで、数珠を2等分するのですから数珠玉の半分を含む半円をイメージします。この半円をカチカチと数珠玉1個分ずつ回転させていくとき、半円の端のペアに着目すると、半円に含まれる白数珠玉の数は1個増えるか、1個減るか、変化しないかのいずれかであることがわかります(図2)。

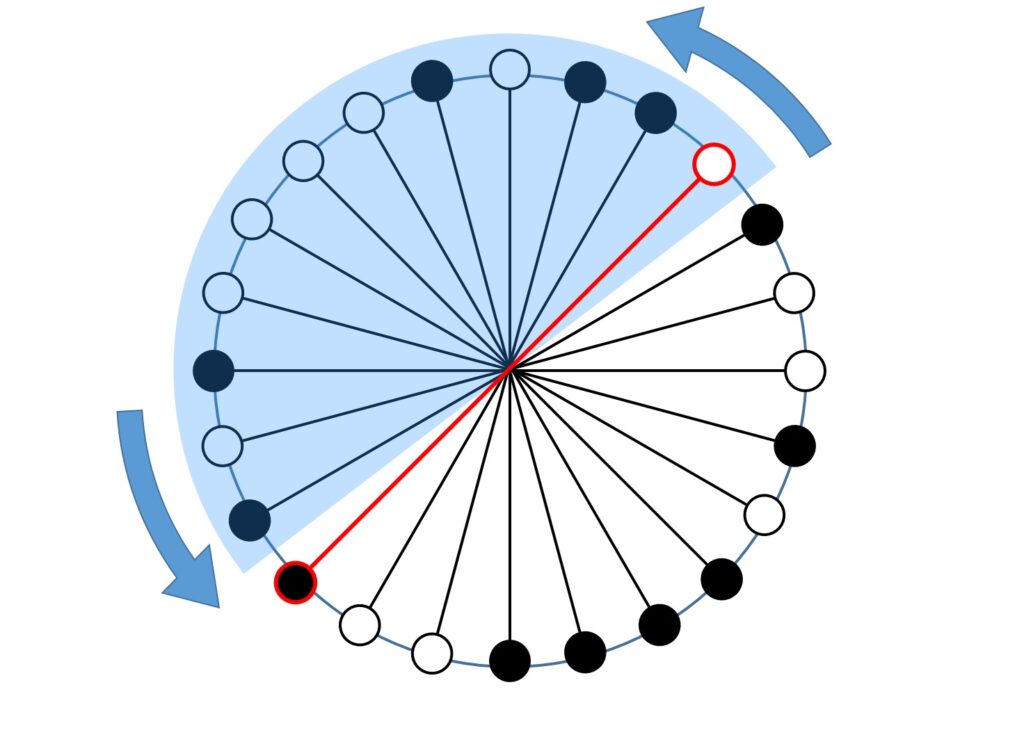
　すなわち、半円の端ペアが白-白の場合、半円に含まれる白数珠玉は1つ減って1つ増えるので増減はありません。また、半円の端ペアが黒-黒の場合も白数珠玉の増減はありません。端ペアが白-黒の場合、白数珠玉が1つ増えて黒数珠玉が1つ減るか、白数珠玉が1つ減って黒数珠玉が1つ増えるかのいずれかです。

　こうして半円を180度回転させます。初期状態の白数珠玉数が m であったとすると、移動後の半円に含まれる白数珠玉は n – m 個になりますが、 m と n – m の間に必ず k が挟まれるので、移動のたびに白数珠玉数は最大1個しか増減しないことを考えると、白数珠玉の数が k 個になるタイミングが必ずあるというのは、中間値の定理的にイメージできるでしょう(図3)。

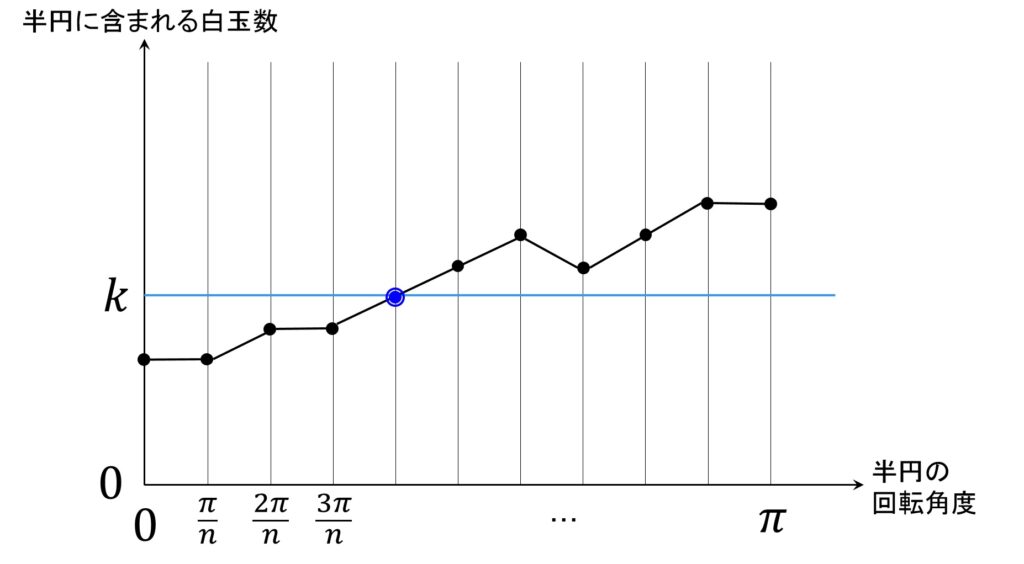
　あとはこれをそれっぽく記述できればOKです。

定式化と証明

　単位円上に 2n 個の数珠玉を等間隔に配置します。整数 l に対し、各数珠玉の座標 a_l を

\begin{aligned}
 &a_l = ( \cos \frac{l \pi}{n} , \sin \frac{l \pi}{n}) \\

\end{aligned}

とします。このとき明らかに a_l+2n = a_l です。

　有限集合 S の要素数を #S と表記するとき、 l = 0,1,…, 2n -1 に対して関数 f(l) を

f(l) = # { l ≦ m < l+n | a_m が白数珠玉 } – k

と定義します。

　すると明らかに、 0 ≦ l ≦ n-1 に対し

f(l) = –f(l+n)

が成り立ちます。したがってもし f(l) > 0 なら f(l+n) < 0、 f(l) < 0 なら f(l+n) > 0 であり、すべての 0 ≦ l ≦ 2n-1 に対して f(l)のすべてが正になったり、負になったりということはあり得ません。

　ここでもしすべての 0 ≦ l ≦ 2n-1 に対して f(l)≠0 であったとすると、f(l) > 0 になる l と f(l) < 0 になる l が必ず同数存在するので、隣り合う l₀ と l₀+1 において f(l₀) と f(l₀+1) の符号が異なるポイントが必ず存在します。

　すなわち、ある 0 ≦ l₀ ≦ 2n-2 が存在して

f(l₀) f(l₀+1) < 0

が成り立ちますが、このとき

|f(l₀) – f(l₀+1) | > 1

です。ところがこれはすべての 0 ≦ l ≦ 2n-2 に対して

|f(l) – f(l+1) | ≦ 1

であることに矛盾します。

　ゆえにある 0 ≦ l ≦ 2n-1 に対して f(l)=0 ですが、もし l ≧ n ならば f(l–n) = –f(l) = 0 なので、 f(l)=0 を満たす l が 0 ≦ l ≦ n-1 であるとして一般性を失いません。この l に対し a_l,a_l+1,…,a_l+n-1 の組に含まれる白玉は k 個、残りの組に含まれる白玉の数も k 個です。

解法のポイント

　本問は問題文をどのようにイメージするかがキモです。均等分割というところから対称性の高い円をイメージするのが第一歩で、2分割というところから半円をイメージし、数珠玉がどのように並んでいても均等分割できるという主張から、半円に含まれる白玉数を中間値の定理的に評価する発想にたどり着くことも重要です。

　さらに半円に含まれる白玉の数は連続関数ではないので、連続性に代わる何らかの縛りも必要です。こういったあれこれをすべて用意するためには、公式を適用して計算すればおけー的な勉強法ではまったく歯が立ちません。

　京大文系数学は理系と同等のガチさを要求しているので、少なくとも赤チャートレベルの問題をスラスラ解けるように、十分に準備しましょう。