「キングオブ難問」1998年東大 数学 後期 第3問の小問2にはいろいろな解法がありますが、主流はいわゆる交代和の剰余類を不変量関数に用いる手法です。
本稿では3次の二面体群を用いた証明を提示するとともに、小問2の主張が二面体群の性質に強く依存していることを示します。交代和の剰余類が不変量関数になるのも二面体群の性質によりますが、本稿ではそれも明らかにします。
なお、本稿の内容は東京大学が発表したものではありません。
1998年東大 数学 後期 第3問 とは
そもそも1998年 東大数学後期第3問 とはどんな問題なのか、ですが、問題文が相当長いので、引用は割愛します。
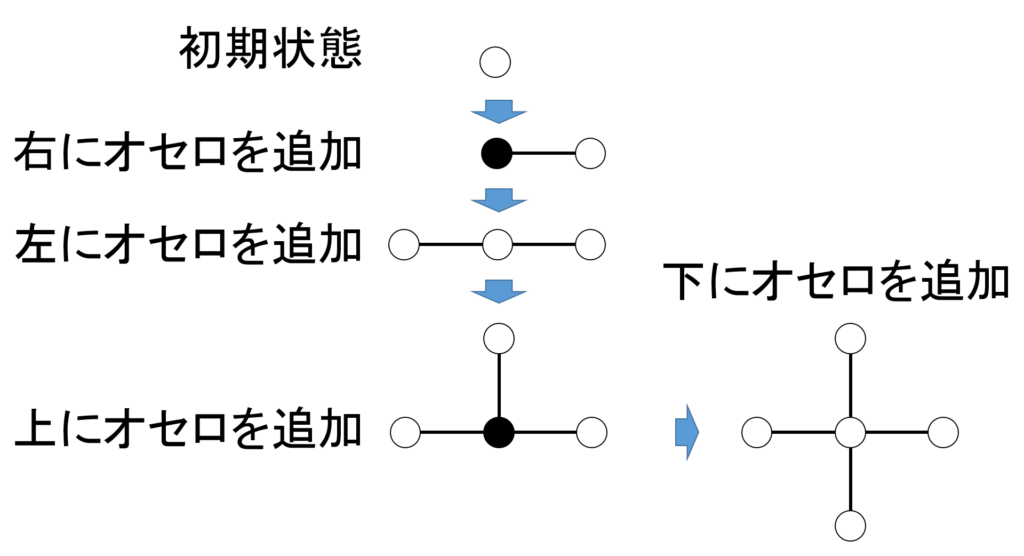
問題の要旨ですが、側面に竹ひごをぷすぷす刺せる、オセロの駒をイメージしてください。このオセロの駒に、竹ひごで別のオセロの駒をつなぎます。1つのオセロに、何本でも竹ひごを刺せるものとします。
オセロの追加方法には、以下の2種類があります。
操作1:オセロ列の端(はし)に対するオセロ追加
オセロ列の一番端に、新しく白オセロを追加します。追加された側のオセロは、色を反転させます。
操作2:オセロ列の中間部に新しいオセロを挿入
オセロとオセロの間に、新しい白オセロを挿入します。もともとあった、両隣のオセロは色を反転させます。
初期状態は、白のオセロの駒が1つだけです。これに上記の要領で、竹ひごとオセロをどんどんつないでいきます(図1参照)。
この問題には、小問が2つあります。小問1は上記のルールに従って以下の図2図形を作成せよ、というものです。小問2は1つの白オセロ石から出発して、左右に操作1または操作2を施してオセロ石が1列に並んでいる状態(本稿ではオセロ列と呼びます)を作るとき、全部の石が白になるための必要十分条件を求めよ、というものです。
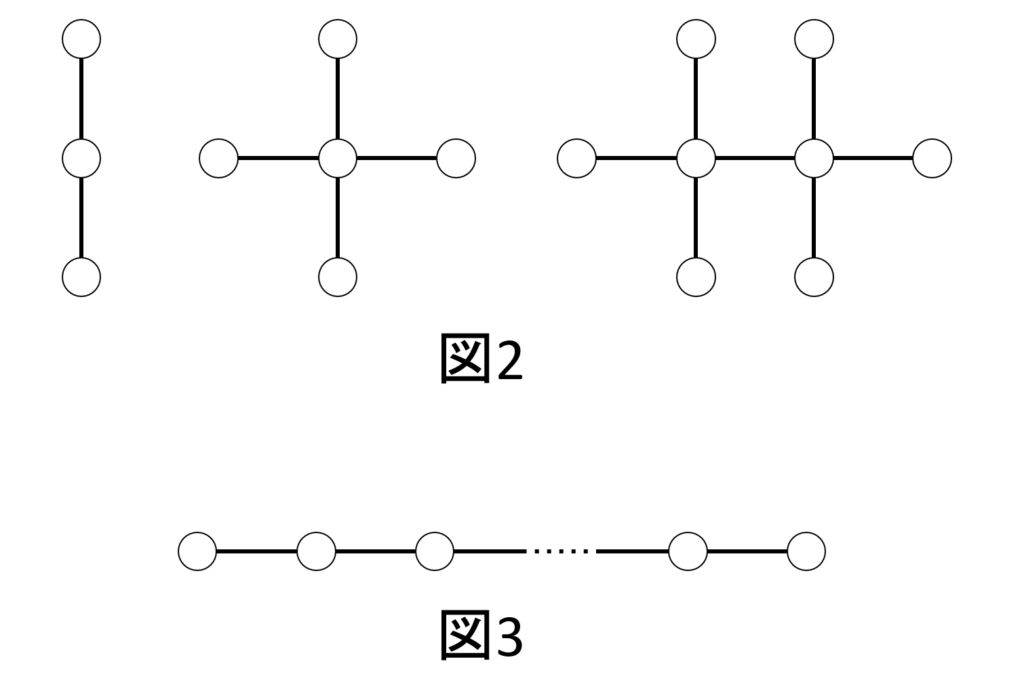
超難問と言いながら、実は小問1は、パズル感覚でさくっと楽しく解けます。超難問なのは小問2の方です。
実はオセロ列の長さ n が3で割り切れるか、または3で割った余りが1の場合は白オセロ列ができることが以下のように比較的容易に証明できます。
長さが n の白オセロ列があるとき、以下の図4の手順によって、長さ n+3 の白オセロ列を生成することが出来ます。

ところが、初期状態は白石1個なので、 n= 3m+1(m=0,1,2,\cdots ) のとき、長さ n の白オセロ列を生成できることがわかります。
また、以下のように長さ n= 3 の白オセロ列を生成できます。
\begin{aligned}
& \text{○} \\
& \Downarrow \\
&\text{●} -\text{○} \\
& \Downarrow \\
\text{○} - & \text{○} - \text{○} \\
\end{aligned}よって n= 3m(m=1,2,\cdots ) のとき、長さ n の白オセロ列を生成できることがわかります。
すなわち、自然数 \bm n を3で割ったあまりが0または1であるとき、長さ n の白オセロ列が生成できます。
一方、 n を3で割った余りが2の時は白オセロ列はできません。これの証明が超絶難問です。
以下、これを二面体群を用いて証明します。
記号の準備
証明に当たって、以下の記号を定義しておきます。
集合の定義
\mathfrak{G} = \{ すべてのオセロ列 \}
G = \{ 1個の白オセロを起点に、操作1および操作2を施して生成されるオセロ列 \}
つまり、 \mathfrak{G} は、特に何も考えずに1列につなげたオセロ列の集合、 G は題意に沿って、1個の白オセロから生成されたオセロ列の集合です。当然、 G \subset \mathfrak{G} が成り立ちます。
拡張オセロ列
オセロ列への操作が2種類あるため、より訳が分からなくなってしまうのですが、仮にオセロ列の「端」がなくなれば、操作1が不要になって、証明が簡素化されることが期待できます。
そこで、初期状態の1個の白オセロの左右に別のオセロ石 o_L,o_R をそれぞれ付け加えて3個状態のオセロ列
o_L - \text{〇} - o_R
にし、これに操作2のみを加えてオセロ列を生成します。こうやって生成されたオセロ列を拡張オセロ列と呼び、その集合を EG と定義します。
EG = \{ o_L -〇- o_R から操作2のみを施して生成された拡張オセロ列 \}
EG も G 同様、 \mathfrak{G} の部分集合です。
EG の各要素は、両端のオセロを1個ずつ取り去ることによって、元のオセロ列集合 G と、操作も含めて1対1対応します(図5)。
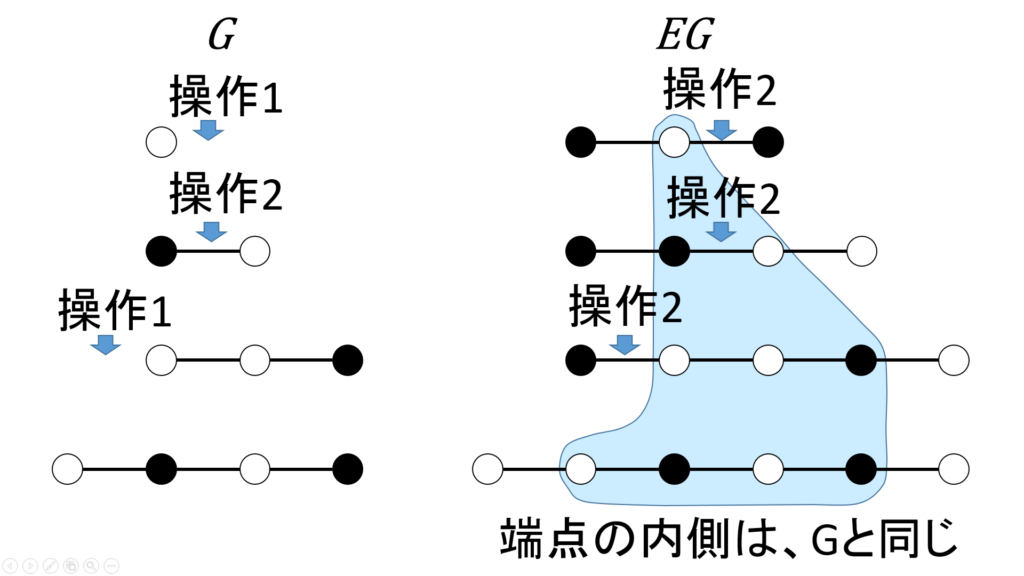
したがって、 g \in G ならば、適当なオセロ石 o_L,o_R を左右に付加したオセロ列 o_L - g - o_R は EG の要素になります。
この対偶を取ることで、以下の命題を得ます。
\bm{g \in \mathfrak{G} } の両端にオセロ石 \bm{o_L,o_R } をどのように付加しても \bm{o_L - g - o_R \notin EG } のとき、 \bm{g \notin G } である
この結果は後で使いますので、覚えておいてください。
3次の二面体群とは
そもそも群とは何か、ですが、集合の一種 G が群であるとは、要素間に何らかの演算が定義されており、その演算によって閉じています(すなわち、演算結果が必ず G の要素になる)。
さらに
- 単位元(足し算における 0 みたいなもの)がある
- 結合法則が成り立つ
- すべての要素に逆元(足し算における、2に対する-2みたいなもの)がある
を満たすものを群と定義します。
これは言葉の定義なのでまあそんなものもあるのかな、くらいの理解で大丈夫です。
そして3次の二面体群の定義ですが、ずばり、正三角形の回転と上下軸に関する反転です(図6)。
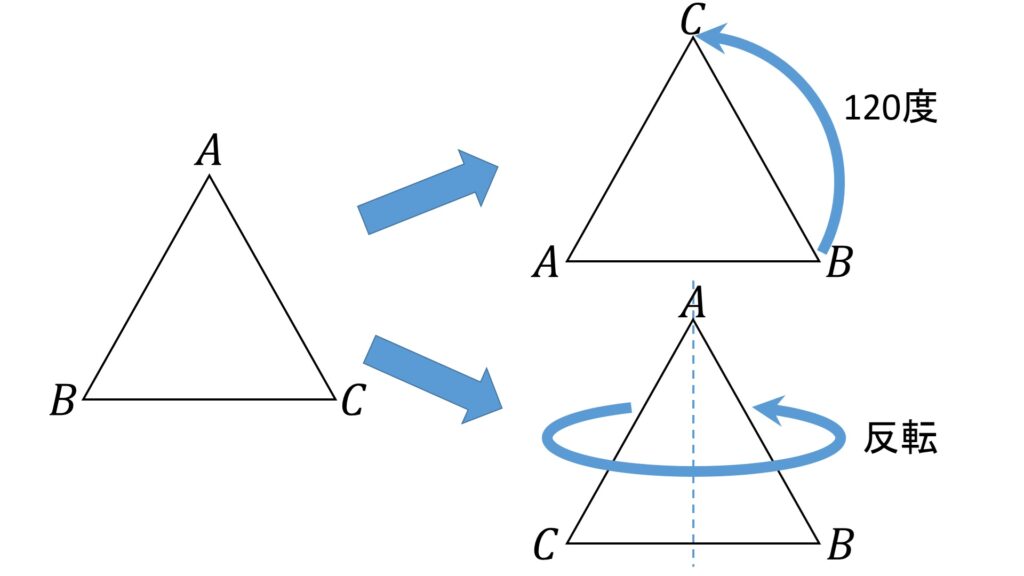
正三角形を自分自身に移す写像は、120度回転、240度回転、反転、120度回転して反転、240度回転して反転、の5種類で、これらに「何もしない」を加えた6種類をどのように組み合わせて作用させても、かならず元の正三角形に移ります(上下さかさまといったことは起きない)。
この回転移動と反転移動には、本問にとって極めて重要な性質があります。すなわち、回転を2回やった結果(つまり240度回転)と、反転して120度回転してもう一度反転した結果は一致します(図7)。

これをもっと数学っぽく表現すると次の通りです:何らかの非可換な演算(演算は普通の文字列の積と同様に表記することにします)によって a^3 = e (e は単位元)を満たす a と b^2 = e を満たす b が存在し、かつ
bab = a^2
が成り立つとき、以下の集合
\{e,a,a^2,b,ba,ba^2 \}は群になりますが、これをこれを3次の二面体群と定義し、 D3 と表記することにします。
なぜ二面体群なのか
ポイントの1つは、白オセロの数を mod 3 で評価することです。 mod 3 ということは白オセロが3つ連続して並んでいたら無いのと同じなので、白オセロを何か3回かけたら1になる的なものに対応させてみると面白いことがわかるかもしれない、という素朴な発想が自然に出てきます。
一方黒オセロのほうは、2つ連続している状態で間に操作2を施すと、白オセロ3つになります。つまり連続する黒オセロ2つは無いのと同じなので、何か2回かけたら1になるようなものに対応させてみます。
そんなわけで白オセロに a^3 = e である a を、黒オセロに b^2 = e である b に対応させると、オセロ列を a,b の演算に自然に対応付けられ、しかもそれは D3 のどれかに必ず等しくなるわけですから、オセロ列そのままよりずっと何かがわかりそうな気がします。
さらに重要なのが、 bab = a^2 です。もう一度オセロ列に対応させると bab は ●-〇-● に、 a^2 は 〇-〇 にそれぞれ対応しますが、 〇-〇 に操作2を施した結果が ●-〇-● なのですから、これはもしかしたらオセロ列を a,b の演算に変換した結果は操作2によって変わらない、すなわちそれこそが不変量関数そのものではないか、と一気に突破口が見えてきます。
不変量関数
そこで拡張オセロ列集合 EG の初期要素を
〇-〇-〇
とし、 EG の要素
g = o_1o_2 \cdots o_n
に対して、 \mathfrak{G} から D3 への写像 f(g) を
\begin{aligned}
f(g) &= d_1d_2 \cdots d_n \\
&\text{ここに} \\
& d_k = \left\{ \begin{aligned} a ( o_k\text{が白オセロ}) \\b ( o_k\text{が黒オセロ}) \end{aligned} \right.
\end{aligned}と定義します。
すると先ほど見たように、
\begin{aligned}
f( \text{操作}2(\text{〇-〇})) = & f( \text{●-〇-●}) \\
= & bab = a^2 \\
= &f( \text{〇-〇})
\end{aligned}が成り立ちます。
一方
\begin{aligned}
ba^2 =b(bab) = b^2ab=ab \\
a^2b =(bab)b=bab^2=ba
\end{aligned}なので、同様にして
\begin{aligned}
f( \text{操作}2(\text{●-〇})) = &f( \text{●-〇}) \\
f( \text{操作}2(\text{〇-●})) = &f( \text{〇-●}) \\
\end{aligned}が成り立ちます。
最後に
\begin{aligned}
f( \text{操作}2(\text{●-●})) = & f( \text{〇-〇-〇}) \\
= & a^3 = e= b^2 \\
= &f( \text{●-●})
\end{aligned}です。
つまり任意の g \in \mathfrak{G} に対し、操作2をどのように施工しても
f( \text{操作}2(g)) = f( g)が成り立つので写像 f(g) は不変量関数であり、任意の g \in EG に対し
f(g) = f( \text{〇-〇-〇}) = a^3 =eなので、 EG の不変量は e です。
n = 3m + 2 のときに白オセロ列ができないことの証明
ここまでくれば、あとは一気に証明できます。
操作2によって黒オセロの数は2つ増えるか、2つ減るか、変わらないかのいずれかなので、操作2によって黒オセロの偶奇は変わりません。
よって、EG の初期要素 〇-〇-〇 の黒オセロ数は0なので、 EG の各要素の黒オセロ数は偶数個です。
したがって長さ 3m+2 (m=0,1,2,…)の白オセロ列 wg \in G が生成できたと仮定するとき、その拡張オセロ列は
ewg_1 =\circ- wg- \circ
か
ewg_2 =\bullet- wg- \bullet
のいずれかです。
ところが
\begin{aligned}
f(ewg_1) & = a^{3m+4} =a \\
f(ewg_2) & = ba^{3m+2} b =ba^2b =b(bab)b =a \\
\end{aligned}なので ewg_1,ewg_2 \not\in EG です。
最初のほうで「 \bm{g \in \mathfrak{G} } の両端にオセロ石 \bm{o_L,o_R } をどのように付加しても \bm{o_L - g - o_R \notin EG } のとき、 \bm{g \notin G } である」という命題を導き出しましたが、これによって wg \not\in G であり、オセロ列の長さ n を3で割った余りが2の時は白オセロ列はできません。
