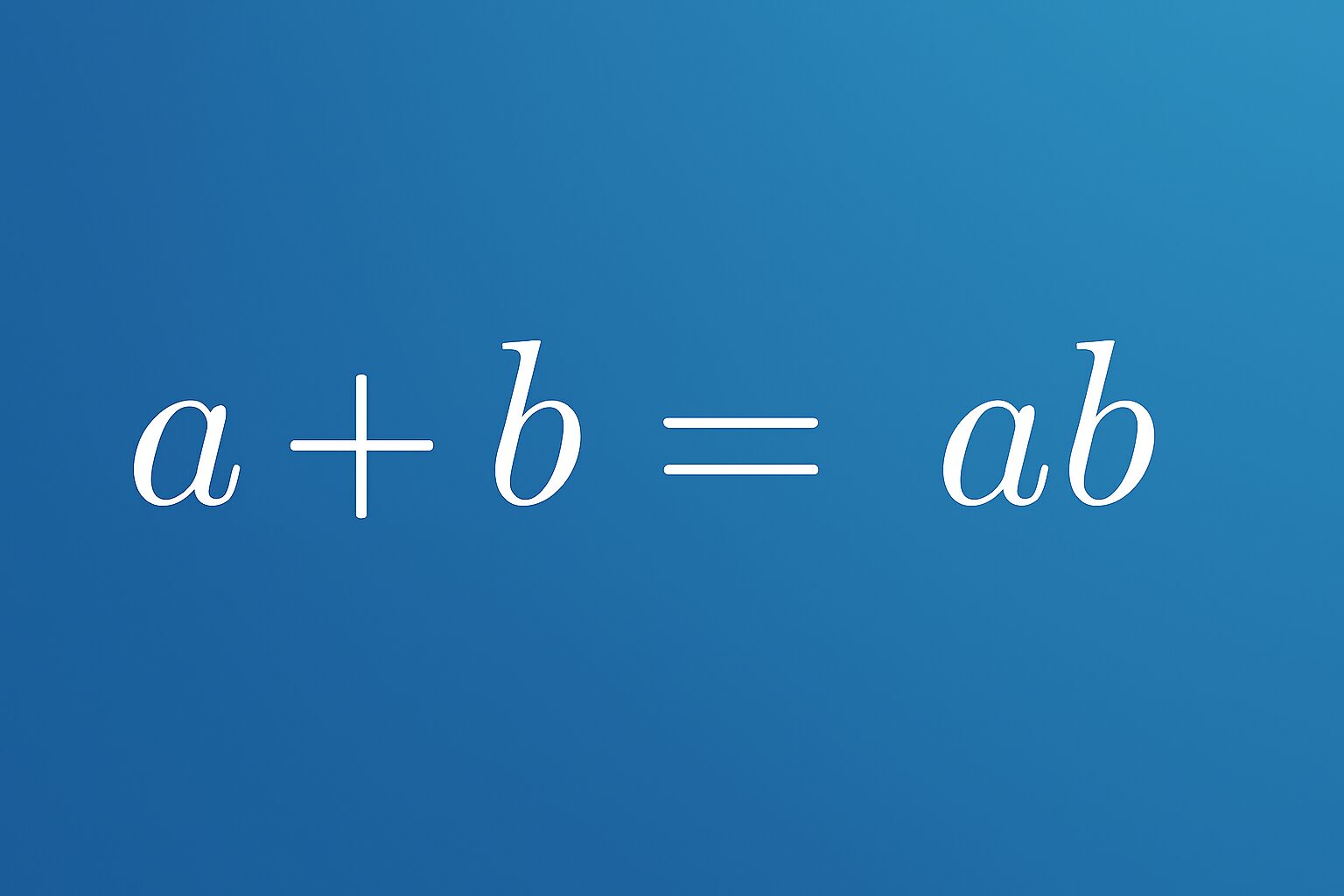n 変数対称式の自然数解 – 1996年 東工大 数学 第1問

　1996年 東工大 数学 第1問 はn 変数対称式の自然数解に関する問題です。問題文は以下の通りです。

　対称式の問題ですが、 n 次というところが曲者です。解が自然数であるという縛りをよりどころに、答えを探っていきましょう。

1996年 東工大 数学 第1問 小問1の解法

　これは問題になれるための小手調べみたいな位置づけの設問です。確実に得点しましょう。

n = 2 の場合

　まず n = 2 の場合です。

　自然 a,b が a + b = ab を満たすときの a,b を求めよ、ということですが、 a = b = 2 がソッコー思いつけると思います。中学や高校で二次方程式は山ほど取り組んできているはずなので、他に自然数解はなさそうだと容易に予測できるでしょう。

　あとはそれをどうやって証明するかですが、

b = \frac{a}{a-1}= \frac{1}{a-1} +1

であることと、 a ≧ 3 のとき \displaystyle\frac{1}{a -1} < 1 であることから、 a ≧ 3 なら b は自然数にならないことがわかります。

　したがって a,b のいずれかが3以上の場合、 a + b ≠ ab です。

　一方、 a,b の双方が 2 以下の場合、いずれかまたは双方が1なら明らかに a + b ≠ ab です。

　ゆえに n = 2 のときの解は

(2,2)

の１種類です。

n = 3 の場合

　次に n = 3 の場合です。

　a,b,c は自然数で、

a + b + c = abc
a ≧ b ≧ c

であるとします。

　a,b,c のすべてが２以上だと等号が成り立たない気がするので、 c = 1 であるとします。

　すると a + b + 1 = ab が成り立つはずですが、 a = 3, b = 2 のときは明らかに等号が成り立ちます。したがって

(3,2,1)

は解の１つです。

　 c = 1 という条件の下で、他に解がないかどうかを考察します。a ≧ 4 とします。このとき、

b = \frac{a+1}{a-1} = \frac{2}{a-1} +1

なので b は自然数になりません。よって 。a ≧ 4 のとき解はありません。

　一方、 (a,b) = (3,3) 、(a,b) = (3,1) や 1 ≦ a,b ≦ 2 のときは明らかに式が成り立ちません。したがって c = 1 のときの解は

(3,2,1)

の1つだけです。

　次に c ≧ 2 の場合です。

　a ≧ b ≧ c ≧ 2 なので

a+b+c \leqq 3a < 4a \leqq abc

です。　等号が成り立たないので c ≧ 2 の場合は解がありません。

　ゆえに n = 2 のときの解は

(2,2)

です。

　順序が違うと別解として扱うので、 n = 3 のときの解は、

(1,2,3)
(1,3,2)
(2,1,3)
(2,3,1)
(3,1,2)
(3,2,1)

です。

1996年 東工大 数学 第1問 小問2の解法

　解が1つしかないということは x_1= x_2 = \cdots = x_n ということなので、ある自然数 a が存在して

na = a^n \cdots(1)

が成り立つような n を求めよ、というのがお題です。

　まず、 n ≧ 2 なので、式(1) が成り立つなら a ≧ 2 であることが必要です。

　次に、小問1から明らかなように、 n = 2 は該当します。

　n ≧ 3 の時はどうなるかですが、一般常識として多項式は x \to \infty のときの増加の度合いで指数関数に絶対勝てないので（証明が必要なので無証明で引用しないようにしましょう）、n が十分に大きいとき

n < 2^{n-1} \cdots(2)

が成り立つと予想できます。

　そこで n ≧ 3 のとき、不等式(2) が成り立つことの証明を目指します。これが証明できれば、任意の自然数 n ≧ 3 と任意の実数 x ≧ 2 に対して

n < x^{n-1}

なので、式(1) を満たす自然数 n ≧ 3 と自然数 a は存在しないことが証明できたことになります。

　これを数学的帰納法で証明します。まず、 n = 3 の時は成り立ちます。

　n ≧ 3 である n に対して式(2) が成り立つとき、

n+1 < 2^{n-1} +1 <  2^{n-1} +  2^{n-1} = 2^{n}

なので、 n+1 に対して式(2)が成り立ちます。

　したがって任意の自然数 n ≧ 3 に対して不等式(2) が成り立つので、式(1) を満たす自然数 n ≧ 3 と自然数 a は存在しません。

　ゆえに解が 1 つしかないような n は n = 2 のみです。

1996年 東工大 数学 第1問 小問3の解法

n = 4 のとき

　まず、 n = 4 のときを考えてみます。

a + b + c + d = abcd

を満たす自然数 a,b,c,d ( a ≧ b ≧ c ≧ d) を探します。

　 a = b = c= d = 1 では明らかに成り立たないですが、 b = c= d = 1 の場合も、 a が何であっても成り立ちません。

　そこで a ≧ b > c = d = 1 であるとします。

　すると a,b が満たすべき式は

a + b + 2 = ab

なので、

b = \frac{a+2}{a-1} = \frac{3}{a-1} + 1

です。よって a,b の両方が自然数になる組み合わせは

(a,b) = (2,4),(4,2)

の2つですが、a ≧ b なので

(a,b) = (4,2)

です。

　一方 a ≧ b ≧ c > d = 1 のときは b ≧ c ≧ 2 であることに注意すると

a+b+c+1 \leqq 3a +1 <4a  \leqq abc

であることがわかります。また、 a ≧ b ≧ c ≧ d ≧ 2 のときも同様に

a+b+c+d \leqq 4a <2^3a  \leqq abcd

が成り立ちます。

　したがって a ≧b ≧ c ≧ d のとき、

a + b + c + d = abcd

を満たす a,b,c,d は

(a,b,c,d) = (4,2,1,1)

の1種類だけです。すなわち n = 4 のとき、解は少なくとも 1 つ存在し，かつ有限個しかないことが示せました。

n ≧ 5 のとき

　上記の結果より、 n ≧ 5 のとき少なくとも

(a_1,a_2, a_3, \cdots,a_n) = (n,2,1,\cdots 1)

は

x_1 + x_2 + \cdots + x_n = x_1x_2 \cdots x_n 

の解であることに気が付けると思います。

　あとは a_1 \geqq a_2 \geqq a_3 \geqq \cdots \geqq a_n \geqq 1 のとき、上記以外の正の整数解が存在しないことが示せればOKです。

　しかしながら、 n = 4 のときと同じようにいろいろ場合分けして確認していくのは、出来なくはないですが少々面倒くさいです。

　もともとのお題は方程式の解が高々有限であることを示すことなので、これをもう少し楽な方法で証明できないか、考えます。

　解の数が有限個だということは、すべての解がある一定の値以下であるということであり、裏返して言えばある値より大きい数字を含む自然数の組は解にならない、ということです。この方向で証明方法を探ります。

　a_k (k = 1,2,…,n) のどれかが少しずつ大きくなる時、 a_1 + a_2 + \cdots + a_n よりも a_1a_2 \cdots a_n のほうが、積なのでより多く増加する気がします。したがってある自然数の組 (a_1,a_2, \cdots , a_n ) に対して

a_1 + a_2 + \cdots + a_n < a_1a_2 \cdots a_n 

が成り立つとき、 b_1 \geqq a_1,b_2 \geqq b_2, \cdots ,b_n \geqq a_n であるすべての自然数の組 (b_1,b_2, \cdots ,b_n) に対し、 b_1 +b_2 + \cdots + b_n と b_1b_2 \cdots b_n の差はさらに広がるので

b_1 + b_2 + \cdots + b_n < b_1b_2 \cdots b_n 

が成り立つだろうと予想できます。

　実際、　 b_1 \geqq a_1,b_2 \geqq b_2, \cdots ,b_n \geqq a_n であるすべての自然数の組 (b_1,b_2, \cdots ,b_n) に対し、

\begin{aligned}
 & b_1 b_2 \cdots b_n - (b_1 + b_2 + \cdots + b_n) \\
= &  (b_1 -1) b_2 \cdots b_n + b_2 \cdots b_n  \\
 & - (b_1-1 + b_2 + \cdots + b_n) -1 \\
 = &   (b_1 -1) b_2 \cdots b_n -  (b_1-1 + b_2 + \cdots + b_n) \\
 & + b_2 \cdots b_n  - 1 \\
 \geqq  & (b_1 -1) b_2 \cdots b_n -  (b_1-1 + b_2 + \cdots + b_n) \\
\geqq  & (b_1 -2) b_2 \cdots b_n -  (b_1-2 + b_2 + \cdots + b_n) \\
 & \vdots \\
\geqq  & a_1 b_2 \cdots b_n -  (a_1 + b_2 + \cdots + b_n) \\
= &  a_1( b_2-1) b_3 \cdots b_n  + a_1b_3 \cdots b_n \\
 &-  (a_1 + b_2-1 + \cdots + b_n)  -1 \\
\geqq &  a_1( b_2-1) b_3 \cdots b_n  -  (a_1 + b_2-1 + \cdots + b_n) \\
 & \vdots \\
\geqq & a_1a_2 b_3 \cdots b_n - (a_1 + a_2 + b_3 + \cdots + b_n) \\
 & \vdots  \\
\geqq & a_1a_2  \cdots a_n - (a_1 + a_2 +  \cdots + a_n) > 0\\

\end{aligned}

なので、

b_1 + b_2 + \cdots + b_n < b_1b_2 \cdots b_n 

が成り立ちます。

　ここで、 (a_1,a_2,a_3,\cdots, a_n ) = (n+1,2,1,\cdots ,1) とおきます。すると

\begin{aligned}
 & a_1 +a_2 + a_3 + \cdots +a_n \\
 = & (n+1) + 2 +\overbrace{ 1 + \cdots +1}^{n-2 \text{個}} \\
= & 2n+1 \\
 
\end{aligned}

ですが、一方で

a_1 a_2 a_3 \cdots a_n = 2(n+1)

なので、

a_1 +a_2 + a_3 + \cdots +a_n < a_1 a_2 a_3 \cdots a_n 

が成り立ちます。

　よって、この (a_1,a_2, \cdots,a_n) に対し、 b_1 \geqq a_1,b_2 \geqq b_2, \cdots ,b_n \geqq a_n であるすべての自然数の組 (b_1,b_2, \cdots ,b_n) は

b_1 + b_2 + \cdots + b_n < b_1b_2 \cdots b_n 

を満たし、したがって問題文の方程式の解になりません。自然数の組が一律大きくなるようなら解にならないことが言えたので、題意の証明に大きく近づきました。

　あとはある b_k < a_k となる b_k がある場合です。ほかのb_k がどんなに大きくなっても方程式の解にならないことを示します。

　自然数の組 (c_1,c_2, \cdots ,c_n ) を、ある 1 ≦ k ≦ n に対し c_k < a_k であり、かつ最大値が n+1 以上であるとします。

　このとき、 (c_1,c_2, \cdots ,c_n ) を降順に並び替えた自然数の組を (d_1,d_2, \cdots ,c_n) と置くと、 d_1 \geqq a_1 = n+1 です。

　よって、もし d_2 \geqq a_2 = 2 ならば、 a_k = 1,k=3,4,\cdots, n なのですから、すべての k=1,2,\cdots,n に対し d_k \geqq a_k であり、

\begin{aligned}
 & c_1 + c_2 + \cdots + c_n\\
 = & d_1 +d_2 + \cdots + d_n \\
<  & d_1 d_2 \cdots d_n \\
   = & c_1 c_2 \cdots c_n
\end{aligned}

が成り立ちます。

　また、 d_2 =1 ならば、 d_k = 1,k=3,4,\cdots, n なので

\begin{aligned}
&c_1 +c_2 + \cdots + c_n  \\
 = &d_1 +d_2 + \cdots + d_n  \\
=  & d_1 +\overbrace{ 1 +1 + \cdots +1}^{n-1 \text{個}} \\
= & d_1 +n-1 \\
>  & d_1 = d_1d_2\cdots d_n \\
 = & c_1c_2 \cdots c_n

\end{aligned}

です。すなわち (c_1,c_2, \cdots ,c_n ) は方程式の解になりません。

　よく考えてみると b_1 \geqq a_1,b_2 \geqq b_2, \cdots ,b_n \geqq a_n の場合も b_k の最大値は n+1 以上なのですから、結局のところ、あるb_k が n+1 以上なら方程式の解になりません。

　この対偶を取ることで、自然数の組 (b_1,b_2, \cdots ,b_n) が方程式の解になる必要条件は、すべての b_k,k=1,2, \cdots , n が n+1 より小さいことであることがわかります。そのような自然数の組は有限なので、n ≧ 5 のとき、方程式の解は高々有限個であることが証明できました。

　n ≦ 4 のときに方程式の解が有限個であることはすでに示されているので、任意の n に対して解は少なくとも 1 つ存在し，かつ有限個しかないことが証明できました。

解法のポイント

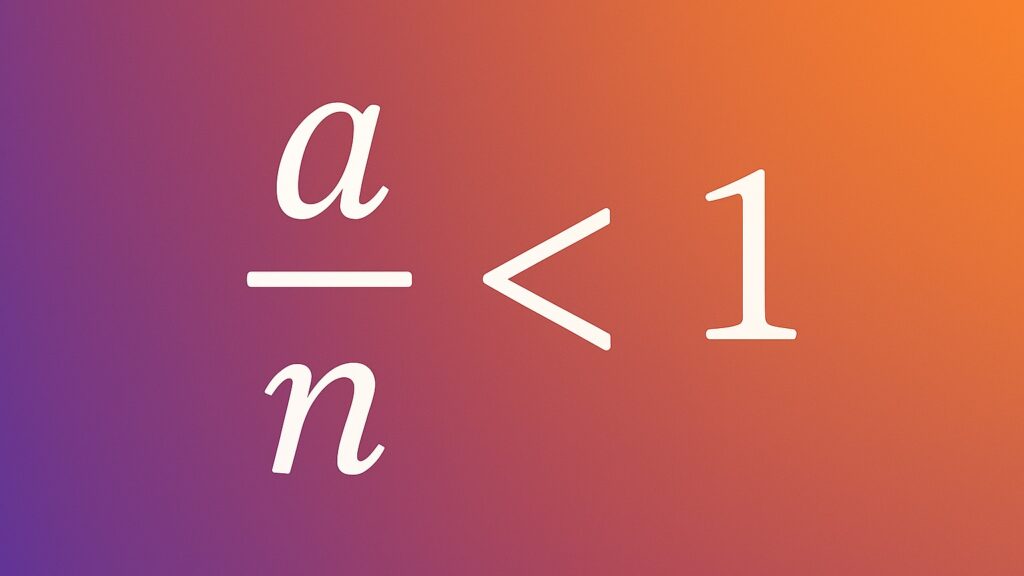
　対称式の問題だと、解と係数の関係から何とかできないかと思いますが、本問の場合はなかなか難しいものがあります。解が整数だという条件から何とかしましょう。方程式に変数の積が現れるので、本稿で示したように分数の項をつくってやって、それが整数になる条件は何だと考えることで解の範囲を絞り込みましょう。