面積の計算は常に「縦かける横」

　二次関数に図形を絡ませた問題として、以下の図1のような三角形AOBの面積を求めさせるものがよく出題されます。

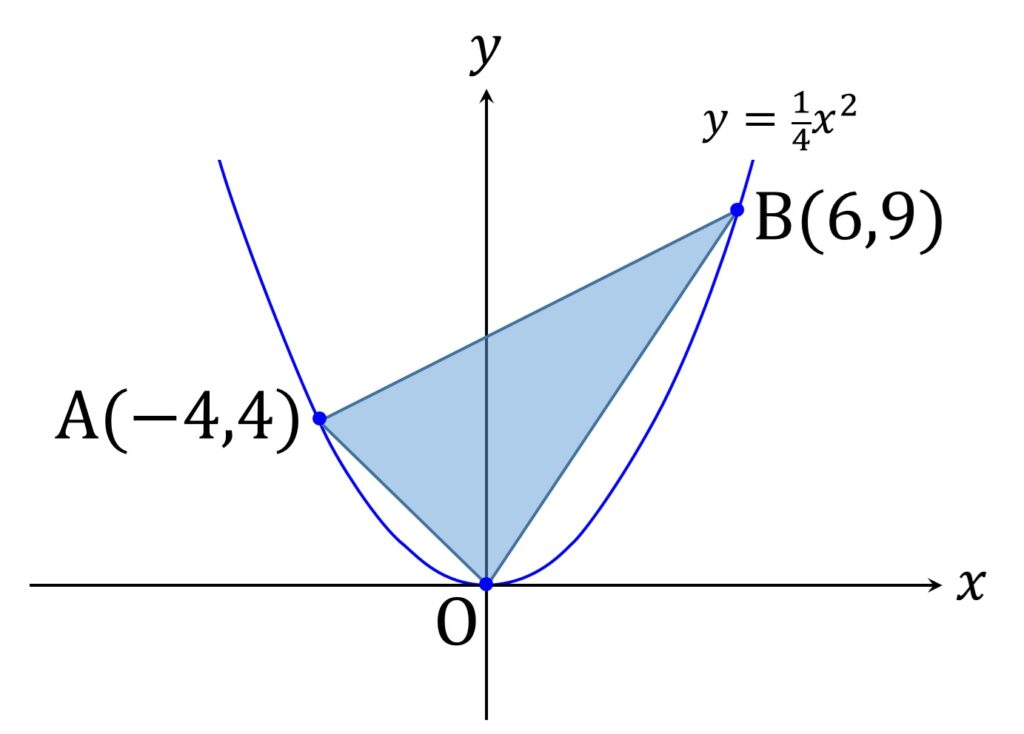
　三角形の面積は小学校で「底辺かける高さ割る２」で教わっているので、このような問題を初めて見た場合など、どうやって計算すればよいか見当もつかない、ということもあると思います。

面積の基本は「縦かける横」

　こういう時は、面積は「縦かける横」で定義されているということを念頭に置くと、突破口が開けてきます。

　何を言っているかというと、面積というのは長方形の面積の求め方「縦かける横」が基本になっている、ということです。三角形や平行四辺形から大学で習うルベーグ積分に至るまで、面積というものは直交する何かの長さの積、すなわち「縦かける横」から求められます。

二次関数と三角形の面積問題に「縦かける横」を適用する

　以上の準備の下に、最初の二次関数の問題に戻ります。面積を求めよという問題の場合、長さが求められてしかも直交する線分の組が必ず存在します。

　そこでそういうものを探すわけですが、このときに重要なことは、グラフの問題というのは直交座標系、すなわち x 軸と y 軸が直交している世界で考える問題である、ということです。

　よって、 x 軸に平行な線分と y 軸に平行な直線をうまく選んでやれば、それらは直交するし長さは端点の座標の差から簡単に求められるので、面積がソッコー求まります。

　図1の場合、辺 AB と y 軸との交点を D と置くと、線分 OD は △AOB に含まれていて、しかも y 軸上にあるのだから当然 y 軸と平行です（図2）。

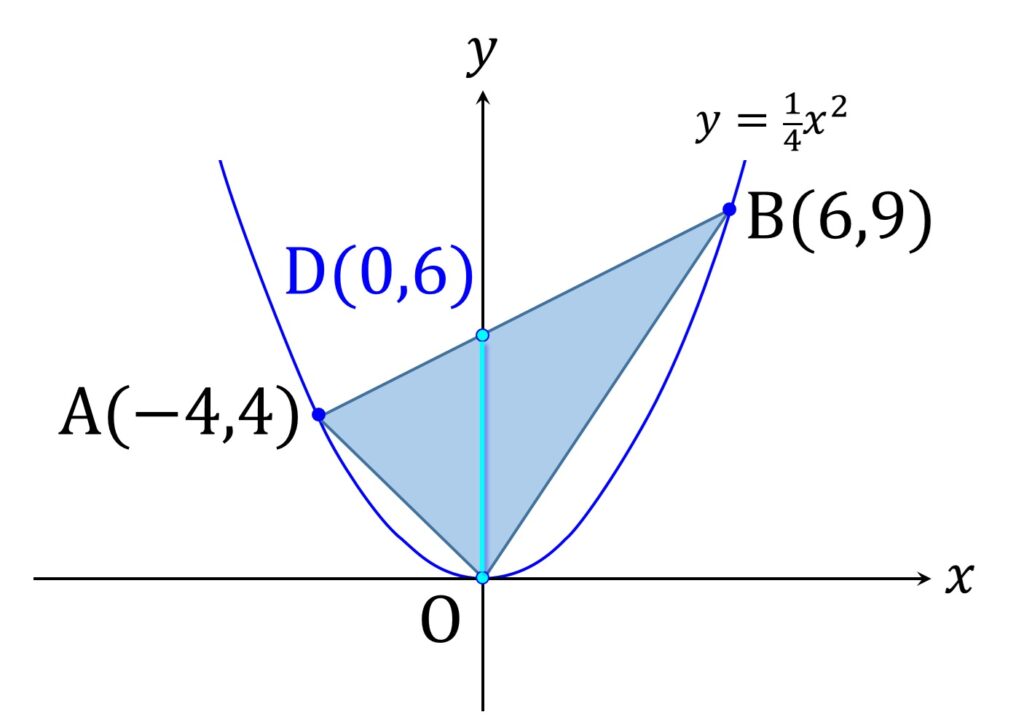
　D の x 座標は 0 、y 座標は2点 A、B を通る直線の方程式の y 切片です。y 切片の値は AB の式を教科書通りにゴリゴリ計算して求めてもよいのですが、もっと楽に計算してみましょう。

　 A から B に到達するには、右に10 、上に 5 移動します。ここからただちに、 AB の傾きが \displaystyle\frac{1}2 であることがわかります。

　よって D は A から右に 4 、上に 2 行ったところにあるのですから、その座標は (0,6) です。

　OD の長さは直ちにわかって、それは 6 です。「縦かける横」の縦の長さがわかりました。

　次に横の長さです。△AOD において OD を底辺と見立てると、高さが横方向になってその値は 4 です。よってその面積は 6 × 4 ÷ 2 = 12 です。

　同様に △BOD の高さは 6 なので、その面積は 6 × 6 ÷ 2 = 18 です。ゆえに △AOB の面積は 12 + 18 = 30 です。

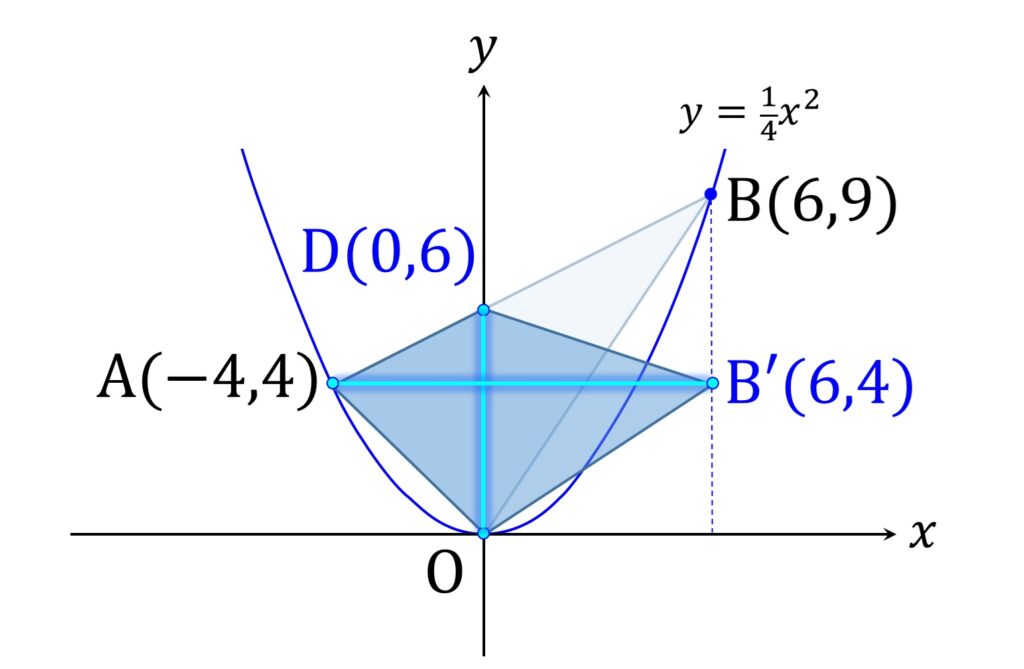
　ここで B を y 軸に平行に動かしても △BOD の面積は変わらないことに着目します。 B を AB が x 軸に平行になる場所に動かして、それを B’ と置きます。

　すると △AOB の面積と □AOB’D の面積は等しくなり、 AB’ が「縦かける横」の横になります。その長さは 10 なのですから、面積は 6 × 10 ÷ 2 = 30 になります（図3）。

二次関数と三角形の面積問題の一般化

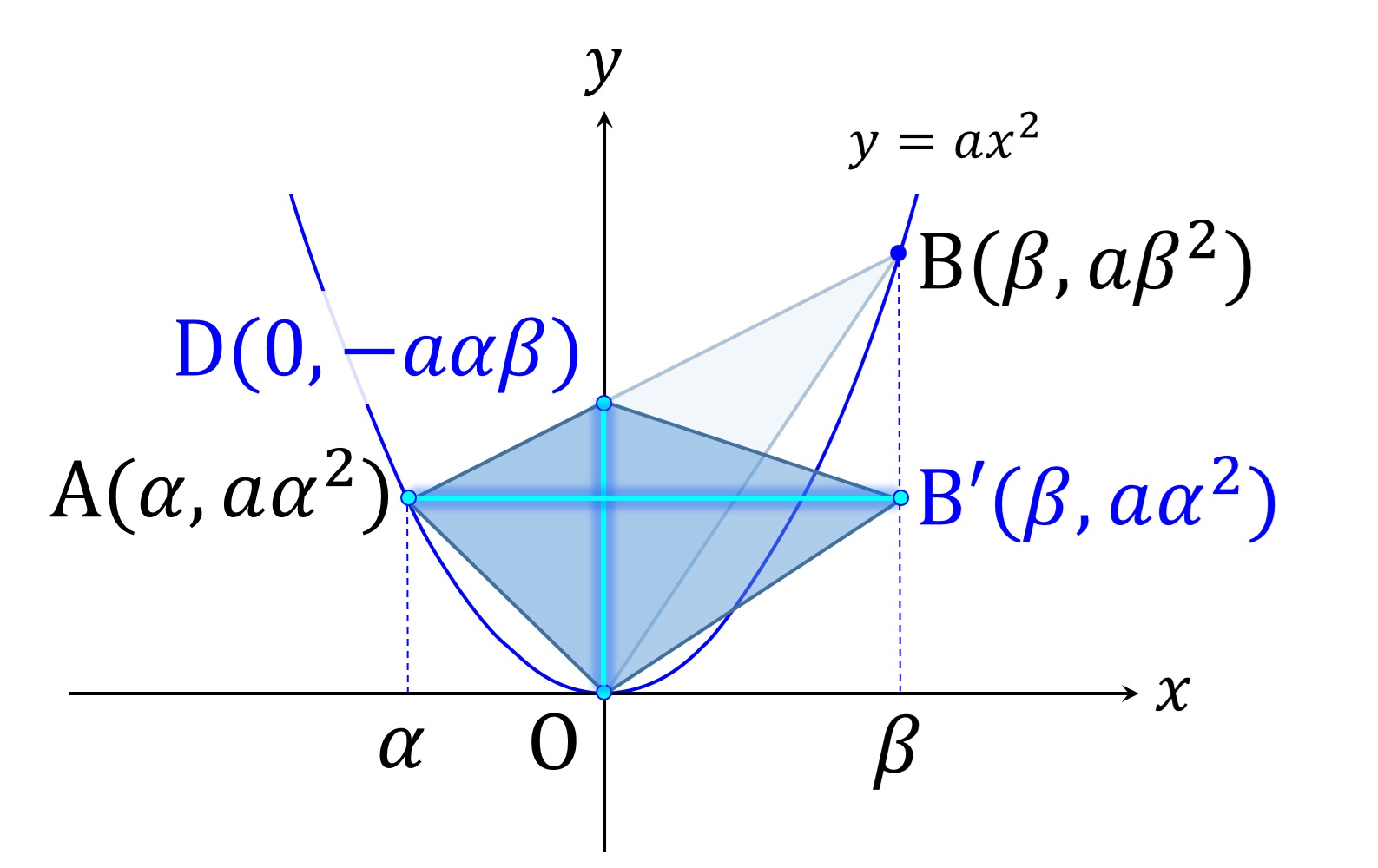
　これを一般化します。ベースとなる二次関数の係数を a とし、 A(α,aα²),B(β,aβ²) であるとき、辺 AB の方程式は

y = a(\alpha + \beta)x - a \alpha\beta

なので、 D(0,-aαβ),B'(β,aα²) です（図4）。

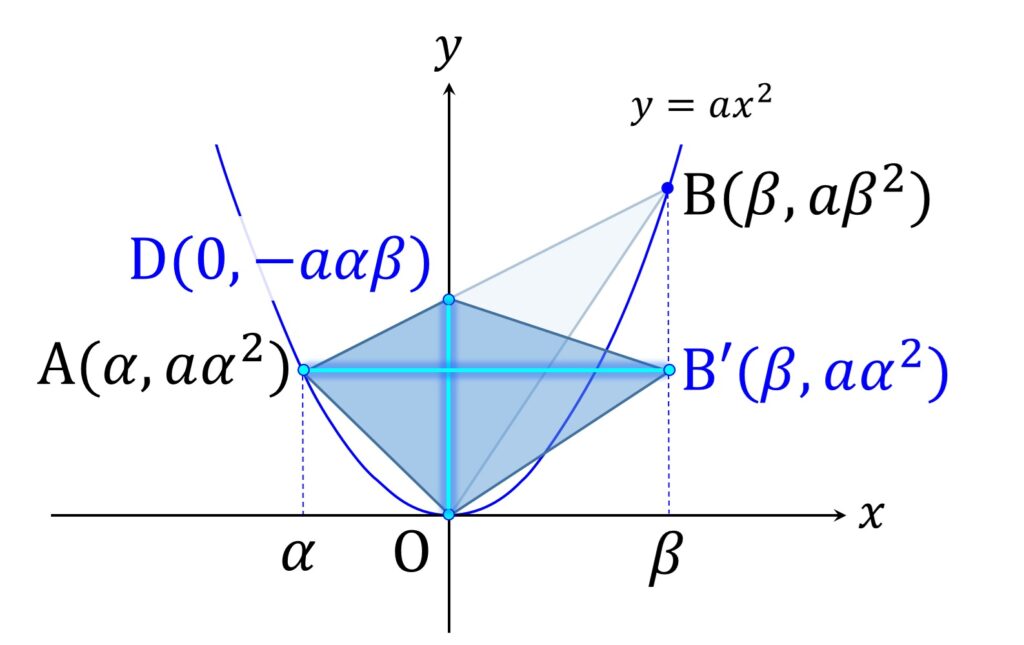
　よって

\begin{aligned}
\mathrm{OD} = &  | a \alpha\beta | \\
\mathrm{AB'} = & |  \beta -  \alpha | \\

\end{aligned}

であり、 △AOB の面積は

 \frac{\mathrm{OD} \cdot \mathrm{AB'}}2 = \frac{1}2 | a \alpha \beta ( \beta - \alpha) |

で求められます。 a、α、βの正負、大小は問いません。

　覚えておくと便利ですが、式それ自体より導出方法のほうを覚えるようにしてください。そのほうが実際の試験においてつぶしが効きます。

三角形のどの頂点も原点でないときの考え方

　次に、三角形のどの頂点も原点でない場合の面積です（図5）。

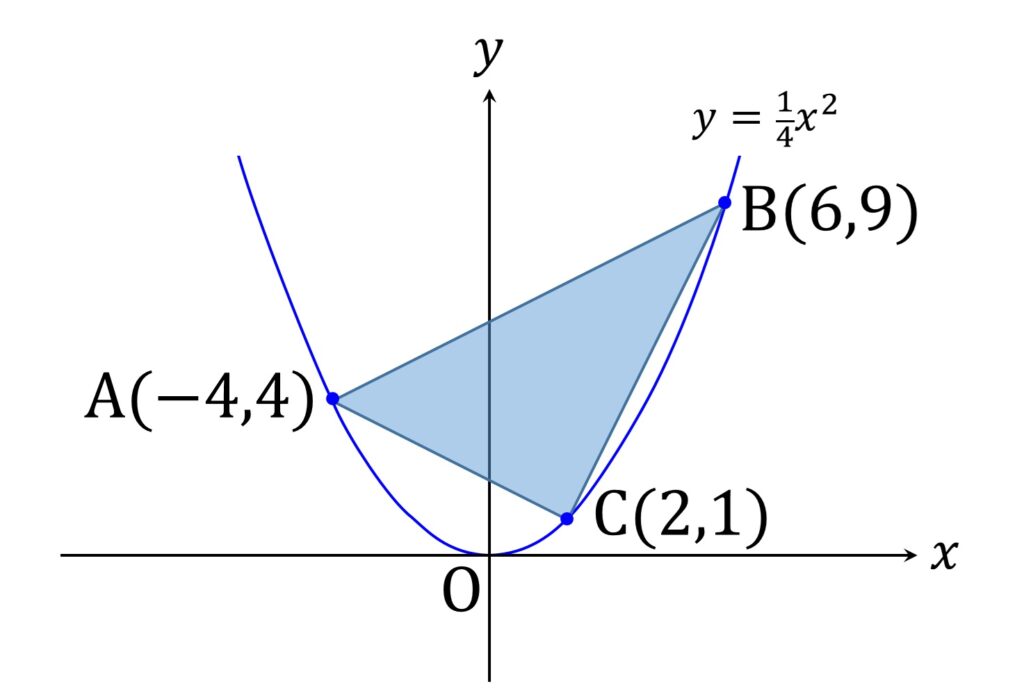
このケースでさらに躓く人が増えますが、考え方は同じです。面積を算出するには「縦かける横」ですが、ぱっと見そんなものはないので、自分で作ります。

　まず縦の線は C を通って y 軸に平行な線と AB の交点を D と置いて、 CD とします。次に横の線は、 A を通って x 軸と平行な直線と、 B を通って y 軸に平行な直線との交点を B’ とおいて、 AB’ とします（図6）。

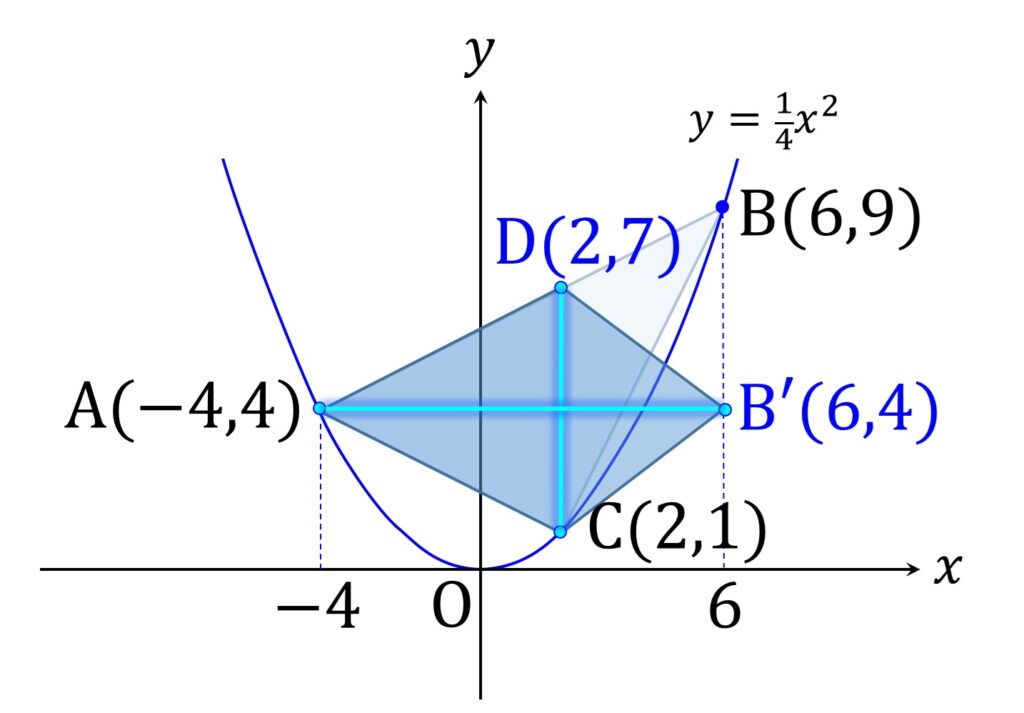
　D の x 座標が 2 であることと、 AB の傾きが \displaystyle\frac{1}2 であることから、 D は A から右に 6 、上に 3 行ったところにあることがわかります。よって D の y 座標は 7 です。

　 CD の長さは 6 、 AB’ の長さは 10 なので、 △ABC の面積は 6 × 10 ÷ 2 = 30 です。

頂点の位置が可変の場合

　頂点 C の位置を可変にするのも定番です。 C の x 座標を t ( -4 ≦ t ≦ 6 ) とおくとき、D は A から右に t + 4 、上に \displaystyle\frac{t+4}2 行ったところにあるので、その y 座標は \displaystyle\frac{t+12}2 です。

　したがって CD = \displaystyle\frac{t+12}2 - \frac{1}4 t^2 であり、 △ABC の面積は

(\frac{t+12}2 - \frac{1}4 t^2) \times10 \div 2 = \frac{5}4(-t^2+2t + 24)

となります（図7）。

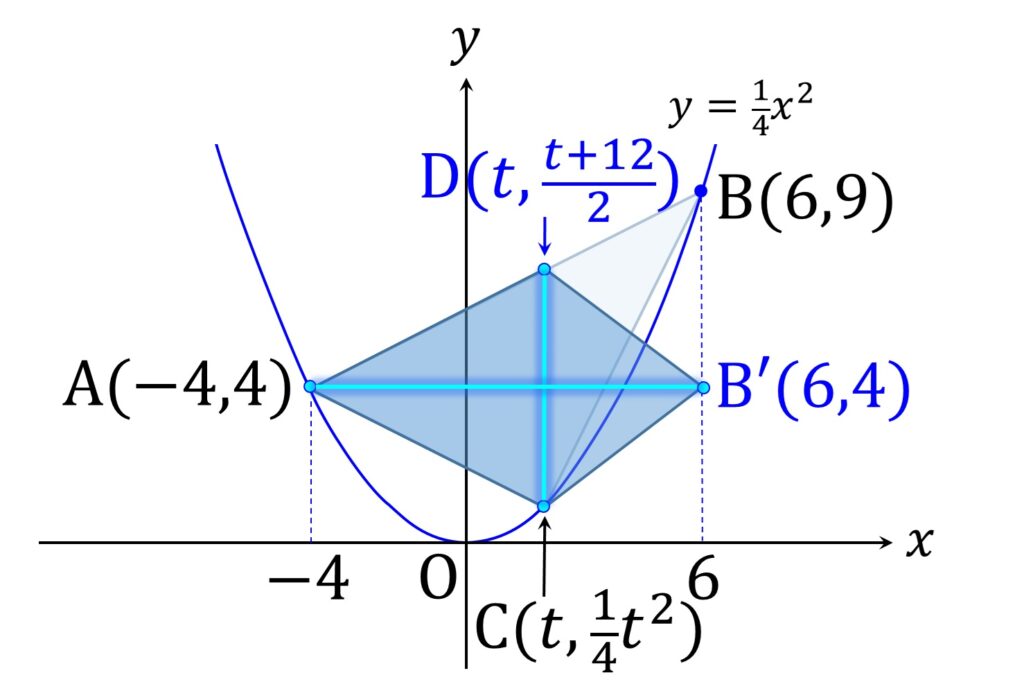
　こういうケースでよくあるのが、 △ABC の面積が 20 のときの t の値を求めよ、といった感じの問題で、

 \frac{5}4(-t^2+2t + 24) = 20 

とおくと

t^2 -2t -8 = 0

なので

t = 4, -2

を得ます。 C(4,4) または C(-2,1) のとき、 △ABC の面積は 20 になります。

　さらに、 △ABC の面積が最大になる t を求めよ、といった問題にも対応可能です。

　二次式の最大値とか最小値を求めよ、とか言われたときはとりもなおさず平方完成です。

 \frac{5}4(-t^2+2t + 24) = - \frac{5}4 (t-1)^2 + \frac{125}4

なので、 t = 1 のときに最大値 \displaystyle\frac{125}4 をとることが直ちにわかります。

三角形の「端の頂点」が可変の場合

　今度は三角形の「端の頂点」を動かしてみましょう。少し難易度が上がります。

　B の x 座標を t (t ≧ 2 ) とおきます（図8）。

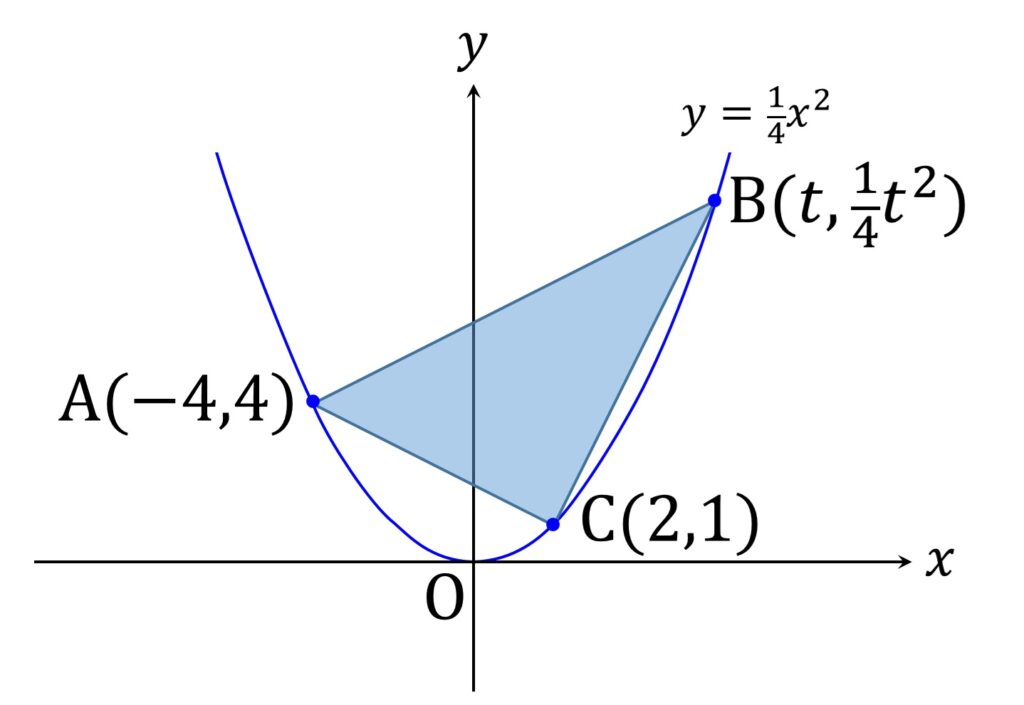
　すると AB の傾きは、 A から右に t + 4 行って上に \displaystyle\frac{1}4 t^2 -4 行ったところに B があるので、

\frac{\frac{1}4 t^2 -4}{t+4} = \frac{1}4(t-4)

です。

　よって D は A から右に 6 、上に \displaystyle\frac{1}4(t-4) \times 6 = \frac{3}2 (t-4) 行ったところにあるので、その y 座標は

\frac{3}2(t-4) + 4 = \frac{3}2t -2

です（図9）。

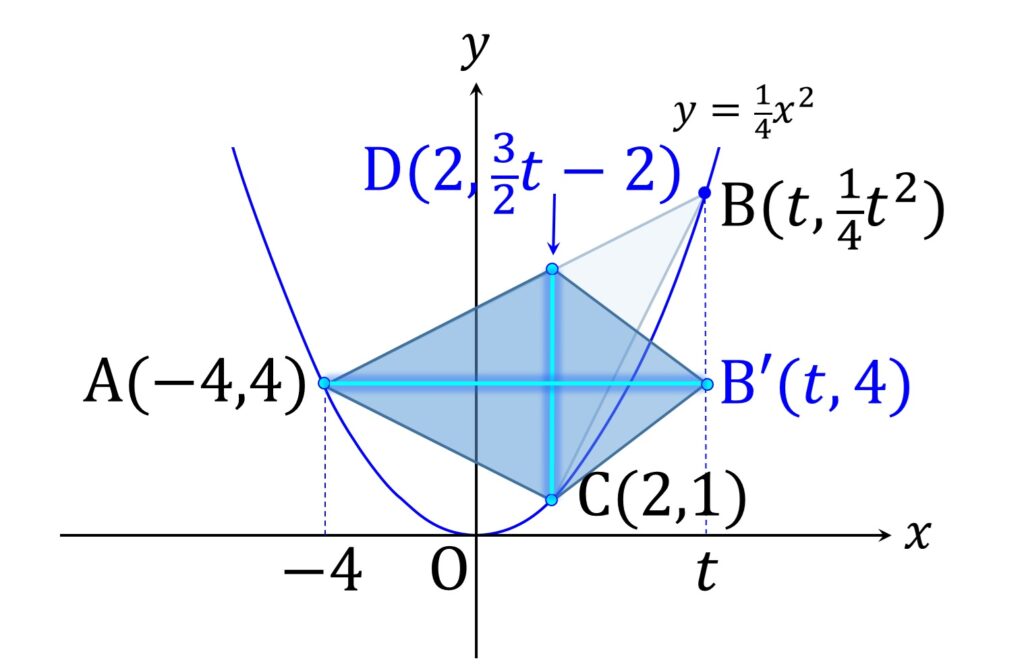
　したがって CD の長さは \displaystyle\frac{3}2 t -3 なので、 △ABC の面積は

(\frac{3}2 t-3) \times (t+4) \div 2 = \frac{3}{4}(t-2)(t+4)

となります。

とにかく「縦かける横」で計算しよう

　二次関数や一次関数に図形がからんで面積を求めよ、といった感じの問題の場合は、とにかく「縦かける横」すなわち、 x 軸や y 軸に平行で長さがわかる線分を見つけ出して、その長さをかけて面積を求めるようにしましょう。