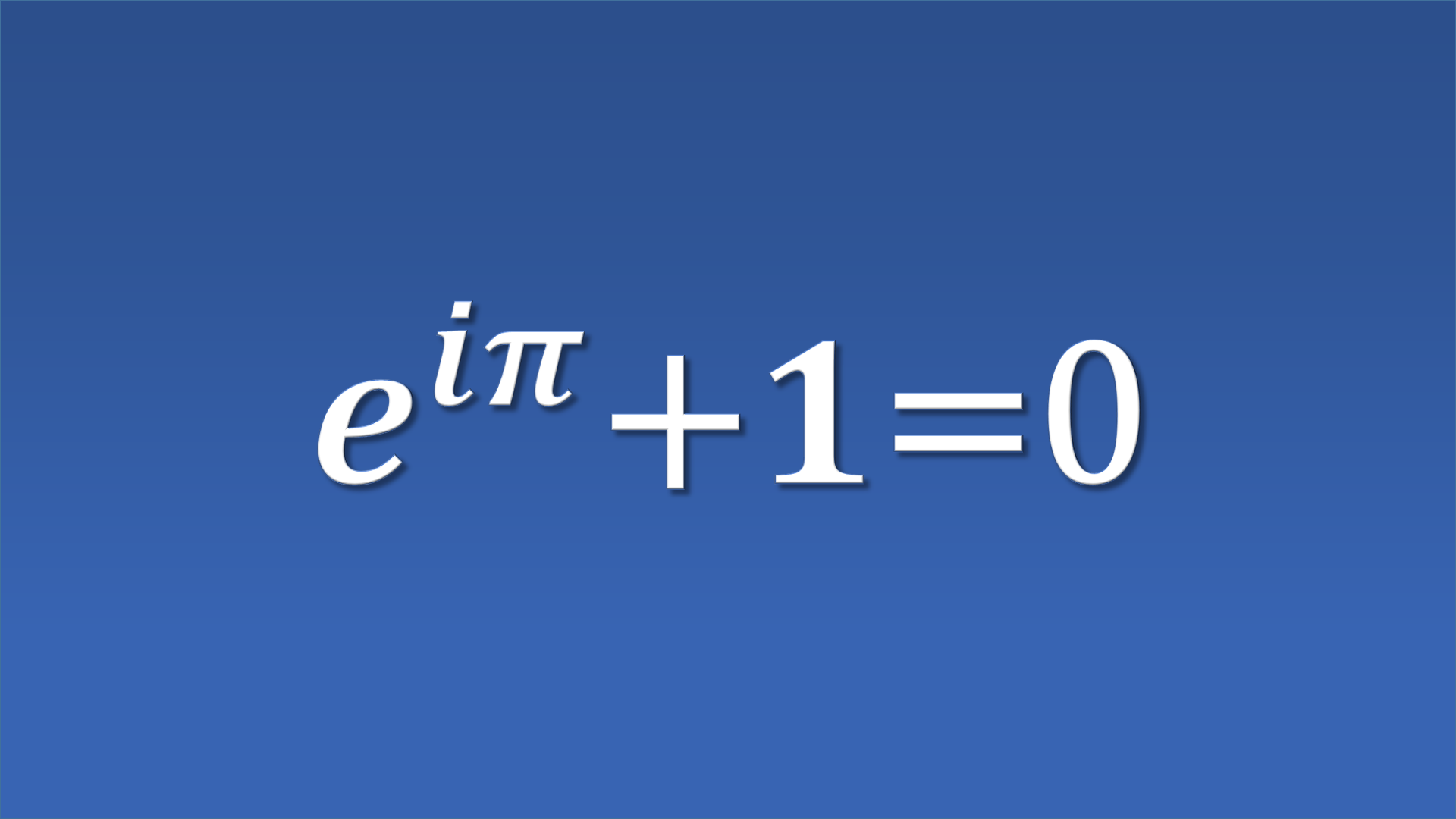2016年京大 文系 数学 第5問 は、3次方程式の複素根に関する問題です。問題文は以下の通りです。
実数を係数とする3次式 f(x)=x^3+ax^2+bx+c に対し、次の条件を考える。
(イ) 方程式 f(x)=0 の解であるすべての複素数 \alpha に対し、 \alpha^3 もまた f(x)=0 の解である。
(ロ) 方程式 f(x)=0 の解は虚数解を少なくとも1つもつ。
この2つの条件(イ)、(ロ)を同時に満たす3次式をすべて求めよ。
条件(イ)に、複素数の3乗が出てきます。本問のように複素数のべき乗が出てきたとき、極形式は無類の強さを発揮します。
極形式とは
極形式とは、複素数 z を複素平面上のベクトルと見立てて、実軸との角度 \theta (偏角と言います)および絶対値 r = |z| で表す表現方式です。以下のように表記されます。
z= r (\cos \theta + i \sin\theta)
極形式は、近年では学習指導要領に復活していますが、筆者が学生時代だった1970年代後半を含む長い間、専門家しか知らない秘密の知識でした。
極形式の何が便利かと言うと、複素数の掛け算が偏角の和、すなわち複素平面上の回転として表現できることです。更には、ド・モアブルの定理という御大層な名前で知られる、以下の公式を簡単に導出できます。
( \cos \theta + i \sin \theta)^n = \cos n \theta + i \sin n \theta
この式を見てしまったら、複素数のべき乗はもう、極形式で表すしかありません。というわけで以下、極形式を使って解いてみます。
2016年京大 文系 数学 第5問 の解法
条件(ロ)と、 f(x) の係数が全て実数であることより、方程式 f(x) = 0 は1つの実数根 x および 2つの虚数根 \alpha 、 \bar{ \alpha} を持ちます。
①実数根
\rho を f(x) =0 の実数解とします。すると、条件(イ)より、 \rho^3 も f(x) = 0 の解あり、しかも実数です。 f(x) = 0 の実数解が1つしか無いことから、
\rho^3= \rho
が成り立ち、したがって \rho は0か1か-1のいずれかです。
②虚数根
次に虚数根 \alpha について考察します。
条件(イ)から導出される、 \alpha が満たすべき式には、以下の2つのバリエーションがあります。
- \alpha^3 が実数根と等しい(ケース1)
- \alpha^3 が \bar{\alpha } と等しい(ケース2)
ケース1についてはさらに、 \alpha^3 = 1 の場合と、 \alpha^3 = -1 の場合に分かれます。なお、 \alpha^3 = 0 の場合は、 \alpha が実数(0)になるので、除外します。
また、 \alpha^3 = \alpha の場合も、 \alpha が実数になるので除外します。
いずれの場合でも、 | \alpha | = 1 が成り立ちます。ケース1の場合は、明らかです。ケース2の場合、
|\alpha|^3=|\alpha|
が成り立ちますが、 \alpha が0のケースを除外すると、 | \alpha | = 1 が成り立ちます。
ところで、 f(x) = 0 の2つの虚数根 \alpha および \bar{\alpha} は互いに共役の関係にあるので、複素平面上において、実数軸に対して線対称の位置にあります。よって、偏角の範囲を 0 から 2π の間で考えるとき、どちらかの偏角は必ず π 未満になります。
したがって、
\begin{aligned}
\alpha = & \cos \theta + i \sin \theta \\
& (0 < \theta < \pi)
\end{aligned}と表記して一般性を失いません。
このとき、ド・モアブルの定理により
\begin{aligned}
\alpha ^3 = & \cos 3\theta + i \sin 3\theta \\
\end{aligned}が成り立ちます。
以下、各場合ごとに、 \alpha の値を求めます。
(1) \alpha^3 = 1 の場合
\left \{
\begin{aligned}
& \cos 3\theta = 1 \\
& \sin 3\theta = 0
\end{aligned}
\right.が成り立ちますが、 0 < \theta < \pi なので \theta = \frac{2\pi}{3} であり、
\begin{aligned}
& \alpha = -\frac{1}{2} + \frac{ \sqrt{3} }{2} i \\
\\
& \bar{\alpha} = -\frac{1}{2} - \frac{ \sqrt{3} }{2} i \\
\end{aligned}となります。
(2) \alpha^3 = -1 の場合
\left \{
\begin{aligned}
& \cos 3\theta = -1 \\
& \sin 3\theta = 0
\end{aligned}
\right.が成り立ちますが、 0 < \theta < \pi なので \theta = \frac{\pi}{3} であり、
\begin{aligned}
& \alpha = \frac{1}{2} + \frac{ \sqrt{3} }{2} i \\
\\
& \bar{\alpha} = \frac{1}{2} - \frac{ \sqrt{3} }{2} i \\
\end{aligned}となります。
(3) \alpha^3 = \bar{\alpha} の場合
\left \{
\begin{aligned}
& \cos 3\theta = \cos \theta \\
& \sin 3\theta = - \sin \theta
\end{aligned}
\right.が成り立つので、これに三角関数の和積の公式を適用して、
\left \{
\begin{aligned}
& -2\sin 2\theta \sin \theta = 0 \\
& 2\sin 2\theta \cos \theta = 0
\end{aligned}
\right.この2つの式を同時に満たすのは、 \sin 2 \theta = 0 の時で、その時の \theta の値は、 0 < \theta < \pi なので \frac{\pi}{2} となります。よって、
\begin{aligned}
& \alpha = i \\
& \bar{\alpha} = -i \\
\end{aligned}です。
③解のまとめ
以上の結果をまとめると、以下の通りです。
| 項番 | 実数根 | 虚数根1 | 虚数根2 |
|---|---|---|---|
| 1 | 1 | -\frac{1}{2}+\frac{\sqrt{3}}{2}i | -\frac{1}{2}-\frac{\sqrt{3}}{2}i |
| 2 | -1 | \frac{1}{2}+\frac{\sqrt{3}}{2}i | \frac{1}{2}-\frac{\sqrt{3}}{2}i |
| 3 | 0 | i | -i |
| 4 | 1 | i | -i |
| 5 | -1 | i | -i |
④求める3次式
方程式の解ごとに、全部で5種類あります。
| 項番 | 3次式 |
|---|---|
| 1 | (x-1)(x^2+x+1) = x^3 -1 |
| 2 | (x+1)(x^2-x+1) = x^3 +1 |
| 3 | x(x^2+1) = x^3+x |
| 4 | (x-1)(x^2+1) = x^3-x^2+x-1 |
| 5 | (x+1)(x^2+1) = x^3+x^2+x+1 |
発展

極形式やド・モアブルの定理は、複素数のべき乗を扱うときに威力を発揮しますが、世の中にはオイラーの公式という、もっとすごいものがあります。
e^{i \theta} = \cos \theta + i \sin \thetaここで \theta= \pi と置くと、更に以下の式を得ます。
e^{i \pi} +1= 0小川洋子「博士の愛した数式」に出てくる式が、これです。
「複素数の指数関数とか、どんな定義になっているんだよ」とか、高校の学習範囲では全く説明がつかない公式ですが、謎の解明は大学に入ってからのお楽しみです。
解法のポイントと今後の学習方針
これまで見てきたように、複素数の掛け算や、べき乗が出てくるときは、極形式の威力が圧倒的です。複素数の計算が楽になったおかげで、本問の場合はむしろ、場合分けを漏らさないことのほうが重要なファクターになっています。昔と違って、極形式は「解禁」になっているので、積極的に使っていきましょう。
学習方針としては、複素平面に関する問題集をやりこむというのが、効果的です。複素平面に漸化式を組み合わせた凶悪な問題もあったりするので、この分野はしっかりマスターしておきましょう。