本稿は前回に引き続き、 2021年京大 数学 第6問 を取り上げます。問題文は以下の通りです。
次の各問に答えよ。
問1 n を2以上の整数とする。 3^n - 2^n が素数ならば n も素数であることを示せ。
問2 a を1より大きい定数とする。微分可能な関数 f(x) が f(a) = af(1) を満たすとき、曲線 y=f(x) の接線で原点 (0,0) を通るものが存在することを示せ。
今回は小問2を扱います。小問1については、こちらをご覧ください。
小問2の定式化
y= f(x) 上の点 (b, f(b)) における接線の方程式は
y= f'(b)(x-b) + f(b)
ですが、これが原点を通るので、それを代入すると
0= -bf'(b) + f(b) \text{ } \cdots(1)を得ます。すなわち、上式を満たす b を見つけることが、本問のゴールです。
平均値の定理の適用
微分が出てきて、何かを満たす値を探せ、みたいな問題が出てきたときは、まず平均値の定理をあたってみましょう。
1 < x < a の範囲で平均値の定理を適用してみると、ある実数 1 < c < a が存在して、
\begin{aligned}
& \frac{f(a) -f(1)}{a-1} \\
&= \frac{af(1) -f(1)}{a-1} \\
&= f(1) \\
&= f'(c) \\
\end{aligned}が成り立ちます。
なんかいい感じじゃね、とも思いましたが、実はこの筋は袋小路です。よく見ると、点 (1,f(1)) と点 (a,f(a)) を結ぶ直線の傾きが f(1) で、それが f'(c) に等しいということを言っているにすぎないことがわかります。
別の関数を定義する
上記の試行錯誤で、(0,0) と (1,f(1)) と (a,f(a)) が1直線上に有ることがわかります。
ここからの発想で、実数 A を傾きとする直線 y = Ax を考えるとき、 A = f(1) ならば y= f(x) と y = Ax は2点 (1,f(1)), (a,f(a)) で交点を持つので、 A の値をうまく決めてやれば、関数曲線 y= f(x) と直線 y = Ax は接するようにできそうだ、と思えてきます。
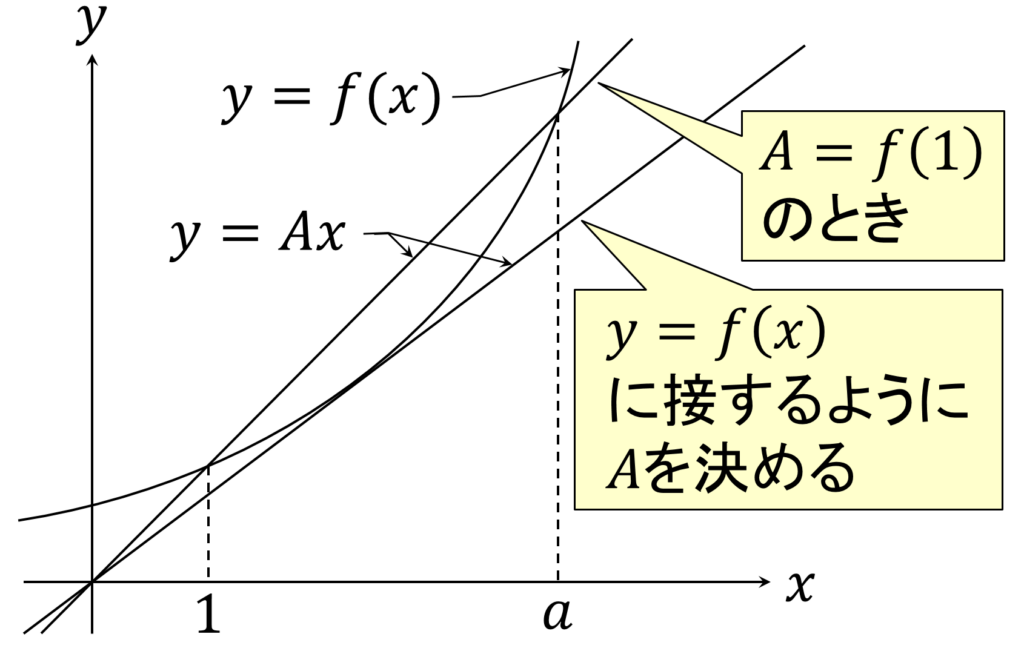
関数曲線と直線の交点の x 座標は
f(x) = Ax
を満たすので、 A は交点の x 座標を用いて
A = \frac{f(x) }{x}と表現できます。
これはすなわち、任意の x \ne 0 に対し A = \frac{f(x) }{x} とおけば、 関数曲線と直線は交点を持つということで、 A は x の関数として定義できるということです。
そこで関数 g(x) を
g(x) = \frac{f(x) }{x}と定義します。 g(x) は x \ne 0 で微分可能です。
平均値の定理ふたたび
g(x) がどういう条件を満たせば、関数曲線と直線が接するようになるか考えているうちに、
\begin{aligned}
& g(1) = \frac{f(1)}{1} = f(1) \\
& g(a) = \frac{f(a)}{a} = \frac{af(1)}{a}=f(1) \\
\end{aligned}であることから、 1 < x < a の範囲で g(x) に平均値の定理を適用すれば何か面白いことが言えるのではないか、とひらめければ勝ちです。
g(x) を微分してみると
g'(x) = \frac{xf'(x) - f(x)}{x^2}ですが、分子に式(1) があからさまに現れているので、この筋は明らかにビンゴです。
すなわち、平均値の定理により、 1 < b < a が存在して、
\begin{aligned}
& \frac{g(a) -g(1) }{a-1} \\
& = \frac{f(1) -f(1) }{a-1} \\
& = 0 \\
& = g'(b) = \frac{bf'(b) - f(b)}{b^2}
\end{aligned}が成り立つので、 式(1) を満たす b の存在が証明できました。
解法のポイント

本問のように、微分可能な関数と、2点に関する情報が与えられたときには、平均値の定理の適用を考えてみましょう。
その上で、本問におけるキーポイントは、 \frac{f(x)}{x} に平均値の定理を適用することを思いつけるかどうか、です。これが思いつければ、本稿に示したように、一気に解くことが出来ます。
式(1) からいきなり \frac{f(x)}{x} を微分してみようと思いつく猛者もいることと思いますが、一般には本稿で示したように、接線の候補となる直線 y = Ax の係数 A が、実は x の関数として表現できるという発想の転換がポイントです。
A の値を振らして最適値を求める問題なので、 A は何に依存して決まるのだろうか、と考えていけば、理詰めで解答にたどり着けることと思います。
