千葉県の公立高校入試問題の傾向が、2022年から大きく変わりました。定番であった規則性の問題が無くなっていたりしますが、本稿で取り上げる第2問は2次関数に図形を絡ませた問題で、これは以前の第3問に対応します。
基本的には、教科書レベルのさくっと解ける問題なのですが、小問3だけが別次元の難しさで、県立入試名物ポイズンピルです。
過去のポイズンピル問題は第4問だったので、本問のような危険な問題がこんな前の方にあるというのも、意表をついています。うっかり拘泥してしまった人もいたかもしれません。
いったいどんな問題なのか、早速見ていきましょう。
2022年千葉県 数学 第2問とは
問題文は以下のリンク先をご覧ください。
本問は2次関数の問題で、3つの小問から構成されています。
図1のように、二次関数 y = \frac{1}{5} x^2 と y = a x^2 (a <0) および長方形 ABCD があります。ここに A の x 座標は5、Bの y 座標は-15です。
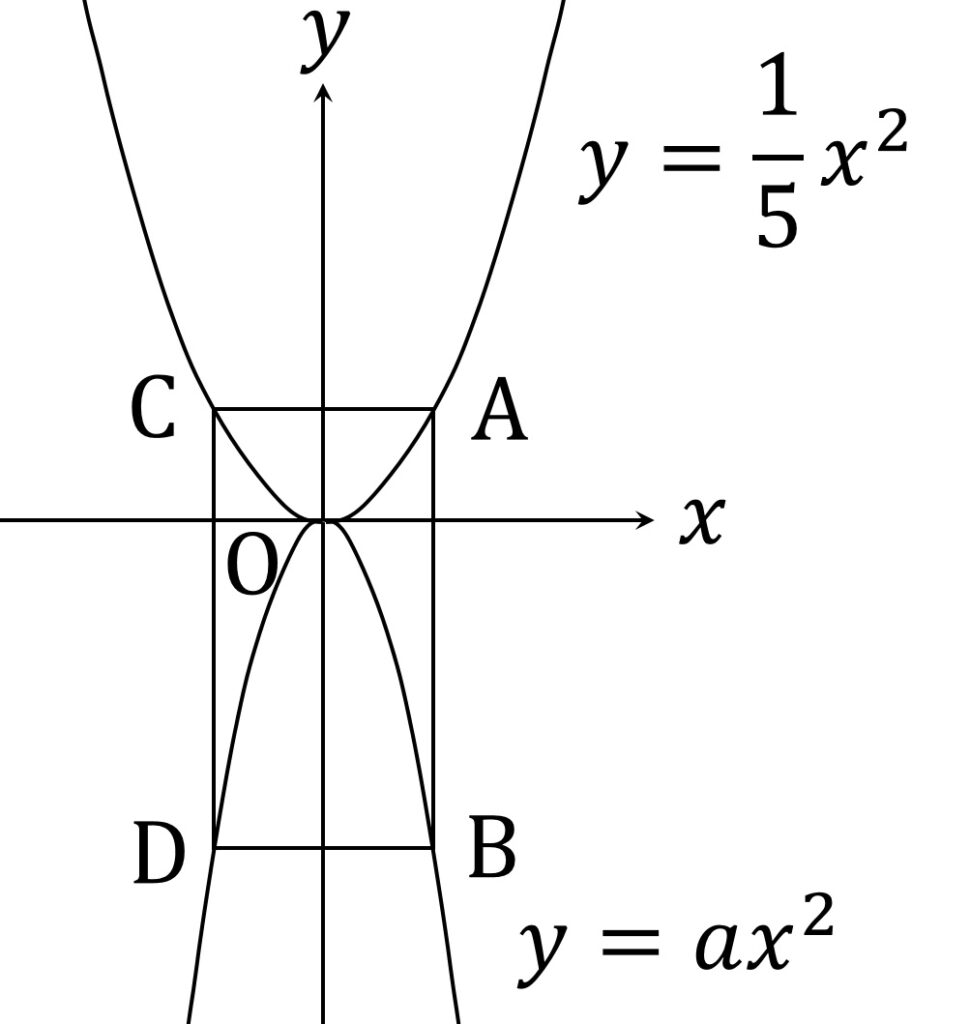
小問1は係数 a の値を求めよ、というものです。また、小問2は2点B、Cを通る直線の式を求めよ、というものです。これらは教科書レベルの、どうと言うことのない問題です。短い時間で正しい答えが出せるようにしましょう。
想定外の難易度の小問3
小問3も同じノリでさくっと解けるだろうと舐めていると、えらい目に遭います。小問3は図2のように、長方形ABCDに合同な長方形DBEFを描いた時、2点E、Fを通る直線の式を求めよ、というものです。
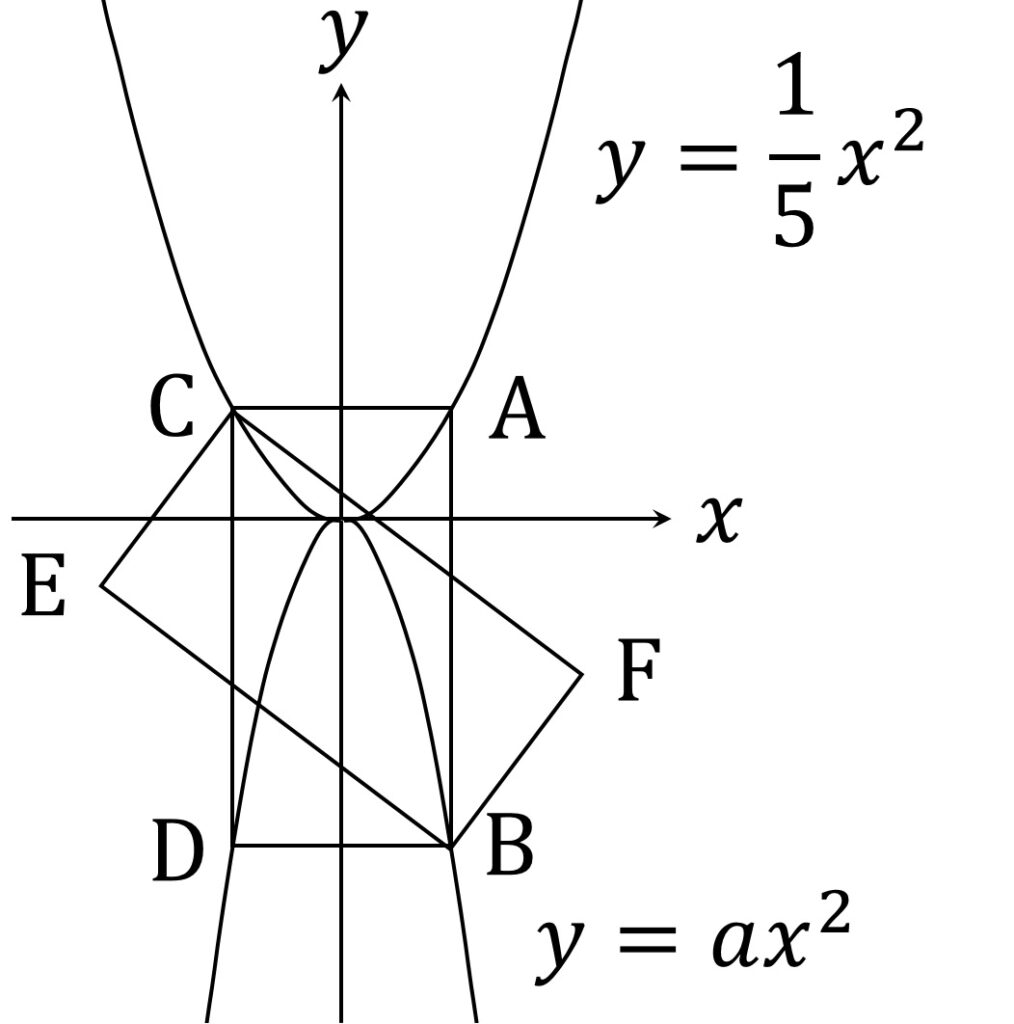
問題の主旨は、長方形ABCDを、その中心(対角線の交点)を軸として回転させてみろ、というものです。座標系の回転は普通、高校でベクトルや三角関数、余弦定理などを使って解くもので、それが高校入試に出てくるのは日常に潜む非日常、ていうか次元断層に足を踏み入れてしまったかのように、背筋に冷たいものが走ります。
実際、解き方がすぐに思いつきません。2次関数の問題として出発したはずなのに、そんなものはどこかに消え失せてしまっています。「容疑者xの献身」に、「例えば、幾何の問題のように見えて、実は関数の問題だとか。少し見方を変えれば解けるはずなんです」なんてセリフが出てきますが、少しくらい見方を変えただけでは、如何ともしようがありません。
小問2の解法
論考の方針
二次関数は不要なので、長方形と座標系にフィーチャーして、図を描きなおしてみます。長方形 ABCD の対角線の交点、すなわち回転の中心を P と置きます(図3)。
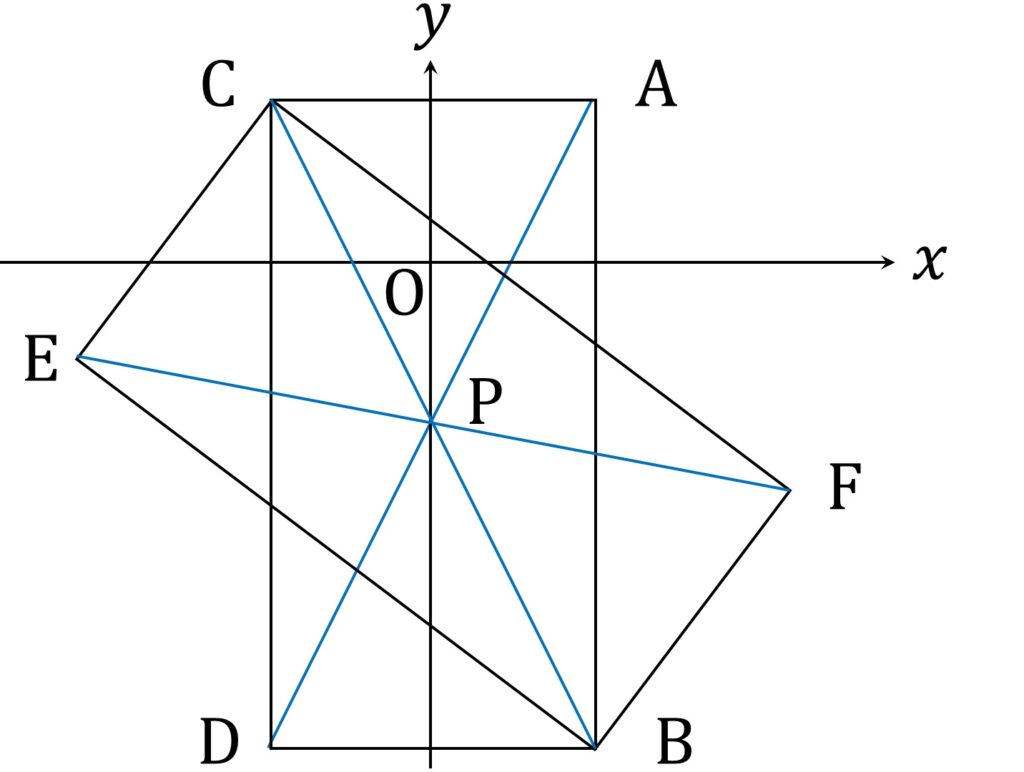
P の座標はあっさり求めることが出来て、それは P(0,-5) です。対角線 EF も P を通るのですから、E または F の座標か、あるいはEF の傾きが分かれば、 EF の式を求めることが出来ます。
いきなり傾きを求めるのは難しそうなので、まずは E または F の座標を求める方針で進めます。ずっと図をにらんでいるうちに、F は B の回転先だが、その回転角は ∠DPB と等しくね?と思いつければ、勝ちです。
実際、△BPF は △DPB を回転させたものなので合同であり、したがって
∠DPB = ∠BPF
PD = PF
が成り立ちます。ゆえに、教科書にも載っていそうな、二等辺三角形の頂角の2等分線が底辺を垂直二等分するって言うのと同じ、基礎的な論考により、
DF ⊥ PB
が成り立つことがわかります(図4)。
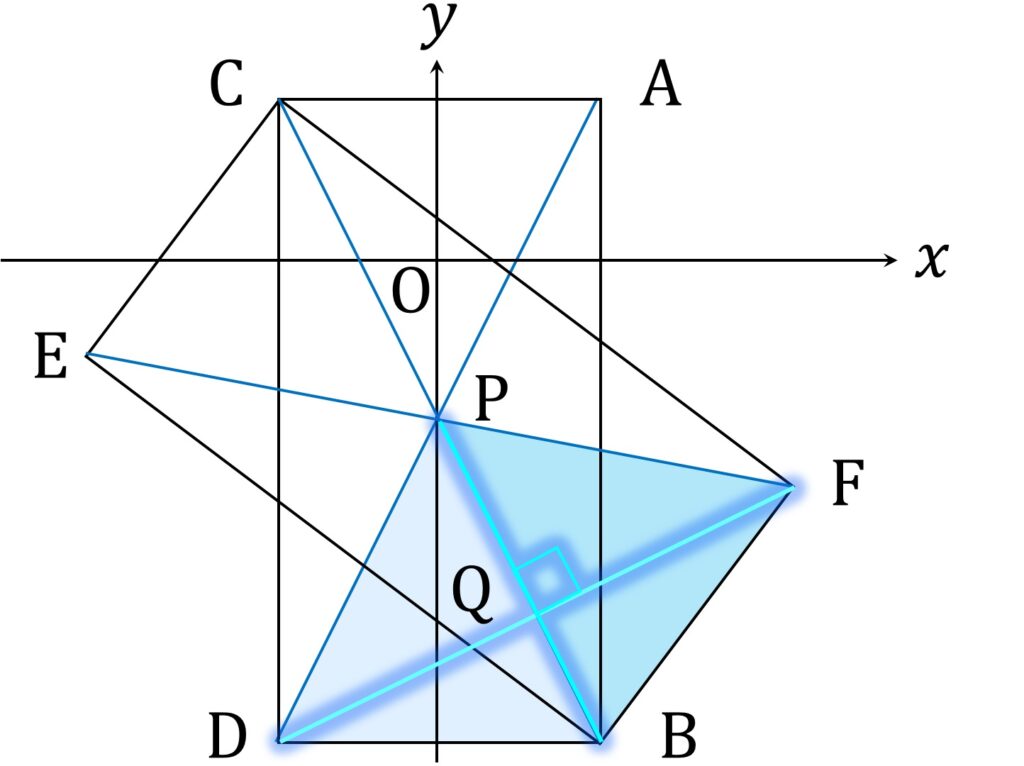
この大いなるグランドクロスの顕現により、点 F の座標を一気に求めることが出来ます。
点 F の座標を求める
DF ⊥ PB であることと、PB の傾きが -2 であることから、DF の傾きは \frac{1}{2} であることがわかります。
このことと、D の座標が (-5,-15) であることから、 DF の式は直ちに求めることが出来て、それは
y = \frac{1}{2}x - \frac{25}{2}です。
あとは地道に、計算するだけです。オーソドックスな進め方は、
- DF と PB の交点 Q を求める
- Q が DF の中点であることを利用して、 F の x 座標を求める
- F の y 座標を求める
といった流れになりますが、点 Q の座標を計算するのが面倒くさいので、三角形の相似を利用してもう少し楽に済ませます。
D を通って x 軸に平行な直線と、 F を通って y 軸に平行な直線の交点を R とします(図5)。
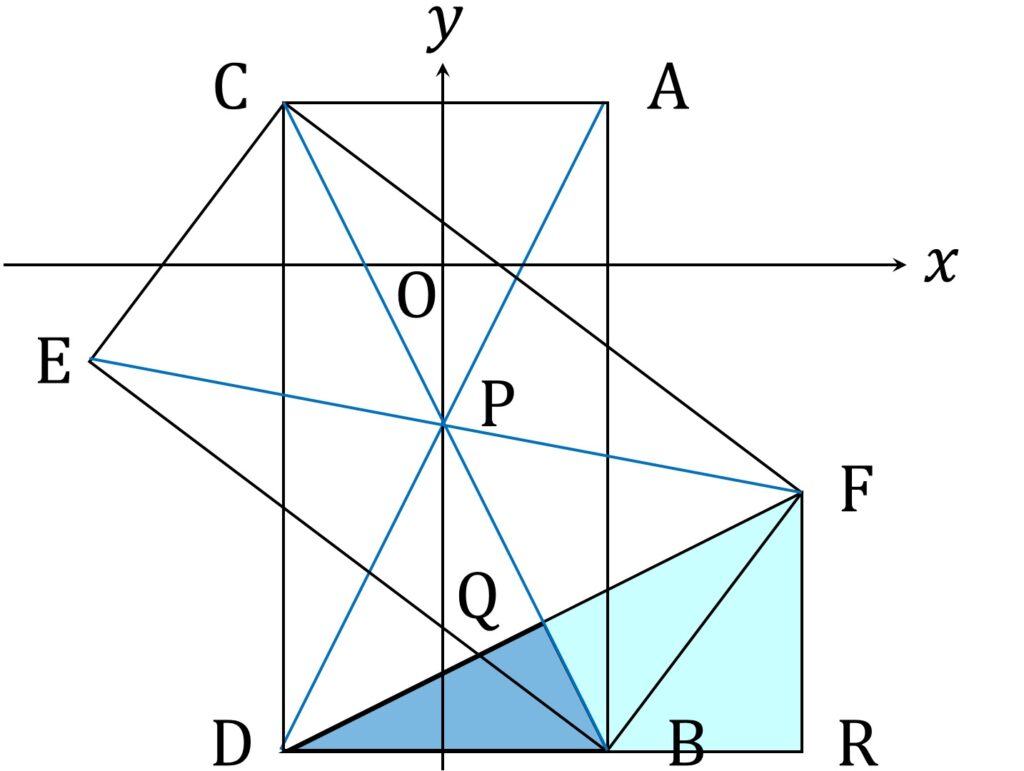
△FDR と △BDQ はいずれも直角三角形で、かつ直角以外の1つの角が共通のため等しいので、2つの三角形は相似です。
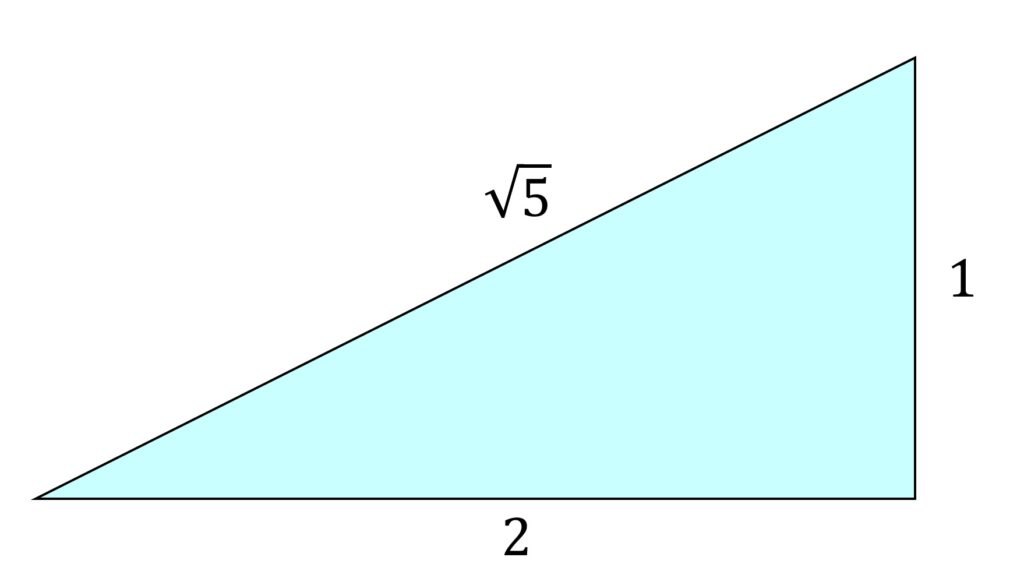
また、DF の傾きが \frac{1}{2} であることから、それぞれの三角形の各辺の比はいずれも 2:1: \sqrt{5} です(図6)。
DR の長さは F の x 座標の値を使って
\mathrm{DR} = x +5と表せます。したがって DF の長さは図6の辺の比からただちに
\mathrm{DF} = \frac{\sqrt{5}}{2}(x +5)と表せます。
点 Q は DF の中点なので、 DQ の長さは DF の半分です。したがって
\mathrm{DQ} = \frac{\sqrt{5}}{4}(x +5)が成り立ちます。
ここで △BDQ に図6の辺の比を適用して
\mathrm{BD} = \frac{\sqrt{5}}{2} \mathrm{DQ}を得ますが、 BD = 10 であることから
\begin{aligned}
10 & = \frac{\sqrt{5}}{2} \cdot \frac{\sqrt{5}}{4}(x +5) \\
& = \frac{5}{8} (x +5)
\end{aligned}が成り立ちます。ゆえに点 F の x 座標は
x=11
です。これを DF の式に代入することにより、点 F の y 座標を求めることが出来て、その値は
y=-7
です。
EF の式を求める
求める直線は P(0,-5) と F(11,-7) を通るので、 y 切片は -5 です。また、傾きは -\frac{2}{11} です。ゆえに直線の式は
y = -\frac{2}{11} x -5です。
解法のポイント

直線の式を求めるには、点 E か点 F の座標を求める必要がありますが、本稿で示したように、 DF と PB が直交することに気が付けば、あとは容易に解くことが出来ます。
これに気が付かなくても、三平方の定理の定理を駆使して解く方法が、ネット上を探せば見つかります。ただ、公立高の入試はとにかく時間との戦いなので、計算量はできるだけ少なくしたいところです。
ある点の座標を求める問題の場合、その点を通る直線が既知の直線のどれかと平行になっていないか、あるいは本問のように直交していないか、注意するようにしましょう。うまくすると、回答時間を節約することが出来ます。
