シリコンウェハーの歩留まり問題 – 2004年 京大 後期 数学 第6問

2022年8月7日2024年9月9日

2004年 京大 後期 数学 第6問 は格子点と極限に関する問題です。問題分は以下のとおりです。

n を自然数とする。xy 平面内の原点を中心とする 半径 n の円の内部と周を合わせたものを C_n であらわす。次の条件を (*) をみたす一辺の 長さが 1 の正方形の数を N(n) とする。

(*) 正方形の 4 頂点はすべて C_n に含まれ、 4 頂点の x および y 座標はすべて整数である。

　このとき

\text{　　　　　} \displaystyle {\lim_{n \to \infty} \frac{N(n)}{n^2} = \pi }

を証明せよ。

　極限値が \pi というのが、嫌げな感じです。大学に行くと、

\frac{ \pi^2}6 = \sum_{n=1}^{\infty} \frac{1}{n^2}

なんていうのが出てきますが、逆に言うと極限値が \pi になる問題は、これくらいしか思いつきません。高校の範囲で本当に解けるのか、泥沼計算が待っているのではないかと、いささか不安になります。

　では早速見ていきましょう。

2004年 京大 後期 数学 第6問 の解法

問題の意味するところを理解する

　式をよく見てみると、 \pi n^2 が C_nの面積であることに気が付きます。また、 N(n) は面積1の正方形の個数なので、それらの面積の合計を意味します。こう考えると、問題文の式の意味するところは、円に完全に含まれる正方形の面積の合計が、 n が大きくなると円の面積それ自体に近づく、というもので、直感的には明らかです。

　昔、日本で半導体産業がもっと盛んだった頃、シリコンウェハーの半径を大きくすると、無駄になる端切れの比率が下がって生産効率が上がる、などという内容の記事を読んだことがありましたが、本問の意味するところは正に、それを数学的にきっちり証明してみろ、ということです。

証明の方針

　まず考えたのが、

1. N(n) < \pi n^2 < N(n+1) が成り立つのではないか
2. N(n+1) - N(n) < \mathrm{C}n （ここにCは定数）が成り立つのではないか

ということです。これらが成り立てば、問題文の式は直ちに証明できます。

　しかし、①や②を証明するには、 N(n) の具体的な式を求める必要がありそうで、これはちょっと無理筋かも知れません。

　そこで、端切れの部分に着目します。すなわち、 n の関数 H(n) を以下のように定義します。

H(n) = 1辺の長さが1でかつ、各頂点の座標がすべて整数の正方形のうち、 C_n の円周が正方形内を通るものの個数

一口で言うと、 H(n) は端切れの個数です（図1の色の濃い正方形の個数）。

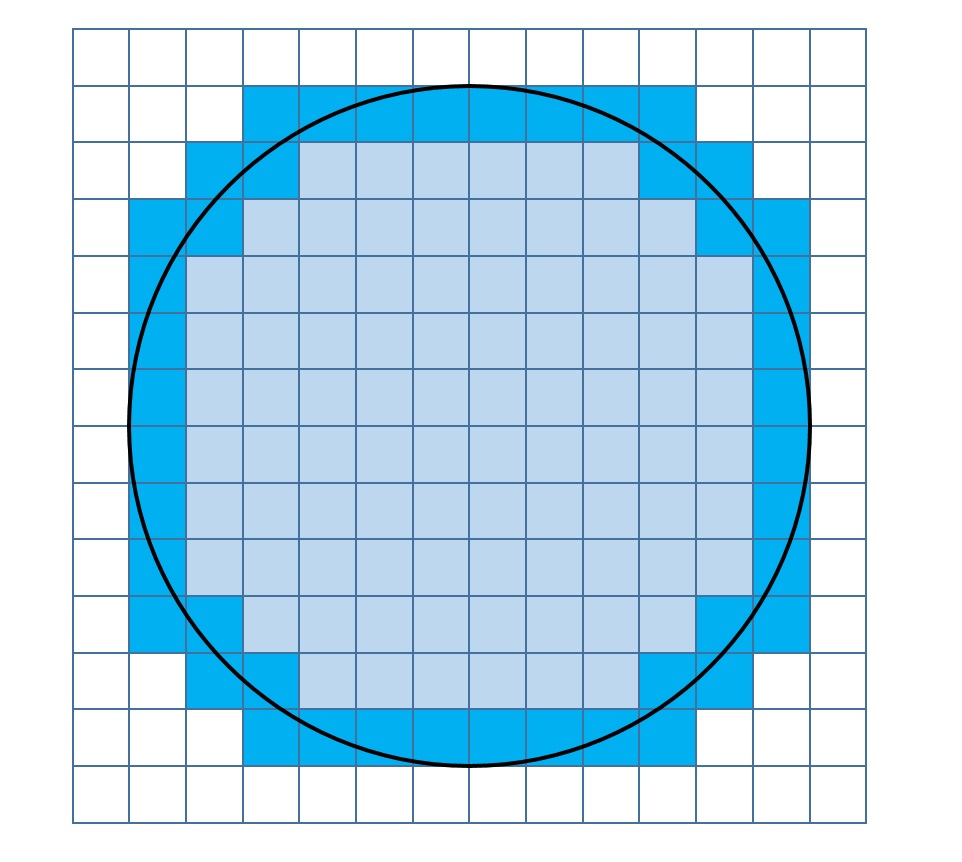
　端切れの分まで含めると、C_n は完全にその中に含まれます。すなわち、

N(n) < \pi n^2 < N(n) +H(n)

が成り立ちます。

　 H(n) は C_n の円周上に乗っている正方形の数なので、円周の長さすなわち2πnに（だいたい）比例するはずです。そこで、n が十分大きい時、ある定数 C > 0 が存在して、

H(n) < Cn

が成り立つことを示します。これが証明できれば、 n が十分大きい時

0<  \pi n^2 -N(n)< H(n) < Cn

なので、

0<  \pi  - \frac{N(n)}{n^2} <  \frac{C}n \to 0(n \to \infty)

が成り立ち、問題文の式が証明できます。

端切れ数 H(n) の評価の証明

　まず、第1象限で考えます（後で4倍すればよい）。

　k を0以上 n -1以下の整数とします。すべての k に対し、 k ≦ x ≦ k+1 の範囲にある端切れ正方形の数は1以上ですが、これが最大でどれくらいかを考えます。

　x がn に近づくに連れて、円周の式 y = \sqrt{n^2- x^2 } の傾きはどんどん小さくなるので、図形全体が y = x に対し対称であることを利用し、 y = x の上側である 0 \leqq x \leqq \displaystyle { \frac {n}{\sqrt{2}} } の範囲で考えます（図2）。

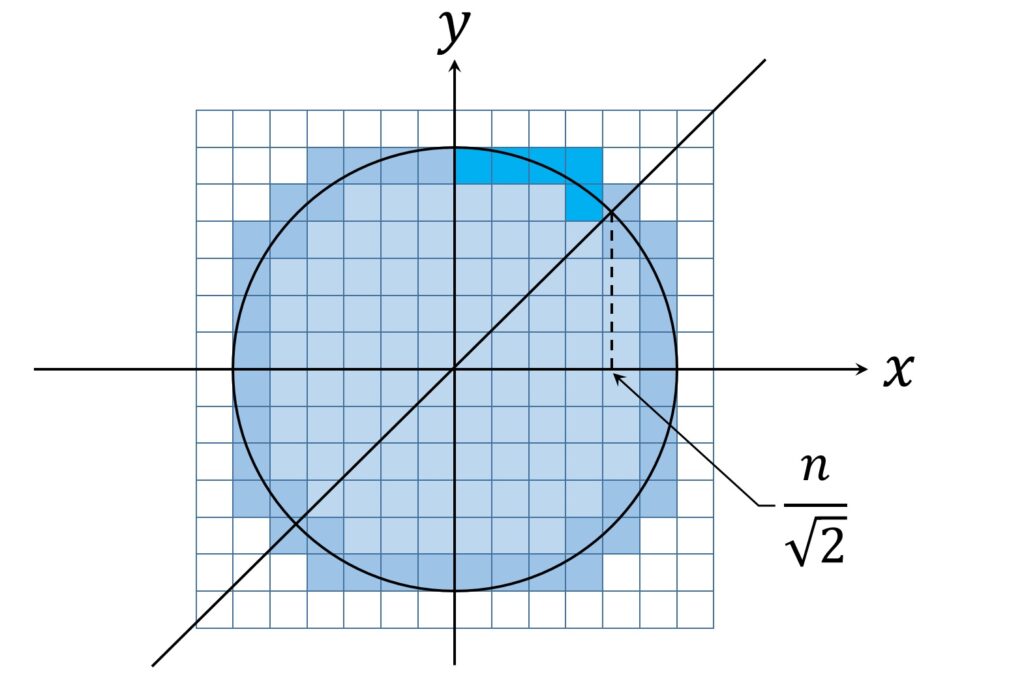
　このとき、円周の傾きは-1以上なので、すべての 0 \leqq k \leqq \displaystyle { \left [ \frac{n}{\sqrt{2}} \right ] -1} に対し、 k ≦ x ≦ k+1 の範囲にある端切れ正方形の数は高々2個です。ここに [] はガウスの記号です。

　したがって、 0 \leqq k \leqq \displaystyle { \left [ \frac{n}{\sqrt{2}} \right ] -1} の範囲にある端切れ正方形の数は、

2 \left [ \frac{n}{\sqrt{2}} \right]  < \sqrt{2} n

で抑えられます。

　次に、 \displaystyle { \frac {n}{\sqrt{2}} \leqq x \leqq n } の範囲で考えます。このとき、円周の傾きは -1 より小さくなりますが、図形全体が y = x に対し対称なので、この範囲の端切れ正方形の数は、 0 \leqq x \leqq \displaystyle { \frac {n}{\sqrt{2}} } の場合と同じです。よって、 \displaystyle { \left [ \frac{n}{\sqrt{2}} \right ] } +1\leqq k \leqq n-1 の範囲にある端切れ正方形の数はやはり、

2 \left [ \frac{n}{\sqrt{2}} \right]  < \sqrt{2} n

と評価できます。

　最後に k = \displaystyle { \left [ \frac{n}{\sqrt{2}} \right ] } の場合ですが、

\begin{aligned}
& \sqrt{n^2-\left [ \frac{n}{\sqrt{2}} \right ]^2} - \sqrt{n^2- \left ( \left [ \frac{n}{\sqrt{2}} \right ]+1 \right ) ^2} \\
\leqq & \sqrt{n^2-\left ( \frac{n}{\sqrt{2}} -1\right )^2} - \sqrt{n^2- \left ( \frac{n}{\sqrt{2}} +1 \right ) ^2} \\
\leqq &  2 \cdot  \frac{ \frac{n}{\sqrt{2}} +1}{\sqrt{n^2-\left ( \frac{n}{\sqrt{2}} +1\right )^2} }\\




\end{aligned}

となります。ここで3行目の不等式は、平均値の定理と円の傾きが単調減少であることを利用しています。

　ここで n > 4 \sqrt{2} のとき、

\begin{aligned}
 & 2 \cdot  \frac{ \frac{n}{\sqrt{2}} +1}{\sqrt{n^2-\left ( \frac{n}{\sqrt{2}} +1\right )^2} }\\
= &2 \frac{ \frac{1}{\sqrt{2}} +\frac{1}{n}}{\sqrt{1-\left ( \frac{1}{\sqrt{2}} +\frac{1}{n} \right )^2} }\\
= & 2 \frac{ \frac{1}{\sqrt{2}} +\frac{1}{n}}{\sqrt{\frac{1}{2}- \frac{\sqrt{2}}{n}-\frac{1}{n^2}}}\\
< & 2 \frac{ \frac{1}{\sqrt{2}} +\frac{1}{4 \sqrt{2}}}{\sqrt{\frac{1}{2}- \frac{\sqrt{2}}{4\sqrt{2}}-\frac{1}{32}}}\\
=& 2\frac{\frac{5}{4\sqrt{2}}}{\sqrt{\frac{7}{32}}} =\frac{10}{\sqrt{7}} < 4

\end{aligned}

　よってこの場合は端切れ正方形の数は高々5個です。

　以上の結果を足しあわせて、第1象限の端切れ正方形の数は、 n が十分大きい時（ n > \frac{5}{3-2 \sqrt{2}} の時）、

\frac{H(n)}4 < 2\sqrt{2} n +5 = (2 \sqrt{2} + \frac{5}n) n < 3 n

と評価できます。

　ゆえに、 n が十分大きい時

H(n) <  12 n

であり、問題文の極限式は証明できました。

解法のポイント

　まず、問題文の式が面積の評価であることに気がつくことがポイントですが、高校数学の範囲でπは円や球の面積、体積の計算くらいにしか使われないので、式の分母を払ってみようという発想は自然に浮かぶことと思います。

　N(n)が円 C_n に含まれる正方形の個数だというところが軽い引っ掛けですが、正方形の面積が1であることから、実はこれも面積を表していることがすぐにわかることと思います。

　次のポイントですが、 \pi n^2 - N(n) の意味するところを、具体的にイメージします。ここで、それが円 C_n から正方形を切り抜いた残りのギザギザ部分、すなわち端切れであることに気が付くことができれば、端切れは n が大きくなれば無視できることは明らかなので、証明の方針が見えてきます。

　端切れがどうして無視できるかと言うと、端切れは C_n の円周に沿って存在し、しかも円周から一定幅のトーラス内であることが明らか（ \sqrt{2} 以上離れたところにある正方形は C_n に完全に含まれるため）なので、その面積は n に比例して増加するだろうと推定できるからです。

　 C_n や N(n) が n² に比例して増加するのに、端切れは高々 n に比例して増加するだけなのですから、 n が大きくなった時無視できるのは、明らかでしょう。あとはそれを具体的に示すだけです。

　このように、何かの式を証明するときには、それが物理的にどういう意味を持つのかを具体的にイメージしてみてください。短い時間で証明方針をつかむことが出来るでしょう。