2022年 京大 特色入試 第2問 は図形の面積に関する問題です。特色入試だからなのか、京大にしてはめずらしく、くどくどと長い問題文になっています。以下の通りです。
半径1の円 C の周上に相異なる5点 A_1,A_2,A_3,A_4,A_5 がこの順に並んでいるとし、
B_1 を線分 A_1A_3 と線分 A_2A_4 の交点、
B_2 を線分 A_2A_4 と線分 A_3A_5 の交点、
B_3 を線分 A_3A_5 と線分 A_4A_1 の交点、
B_4 を線分 A_4A_1 と線分 A_5A_2 の交点、
B_5 を線分 A_5A_1 と線分 A_1A_3 の交点、
とするとき、
S_1 を \triangle A_1B_5B_4 の面積、
S_2 を \triangle A_2B_1B_5 の面積、
S_3 を \triangle A_3B_2B_1 の面積、
S_4 を \triangle A_4B_3B_2 の面積、
S_5 を \triangle A_5B_4B_3 の面積、
T を五角形 B_1 B_2 B_3 B_4 B_5 の面積
とおく。このように A_1,A_2,A_3,A_4,A_5 を動かしたとき、
S = S_1 +S_2 +S_3 +S_4 +S_5 +2T
の最大値を求めよ。
ただし、三角比の値は具体的に求めずに用いてよい。
題意は、問題文の見た目ほど複雑ではありません。要は、 A_1,A_2,A_3,A_4,A_5 を頂点とする五芒星において、星形の角の三角形の面積と、中央の五角形の面積の2倍の和の最大値を求めよ、ということです(図1)。
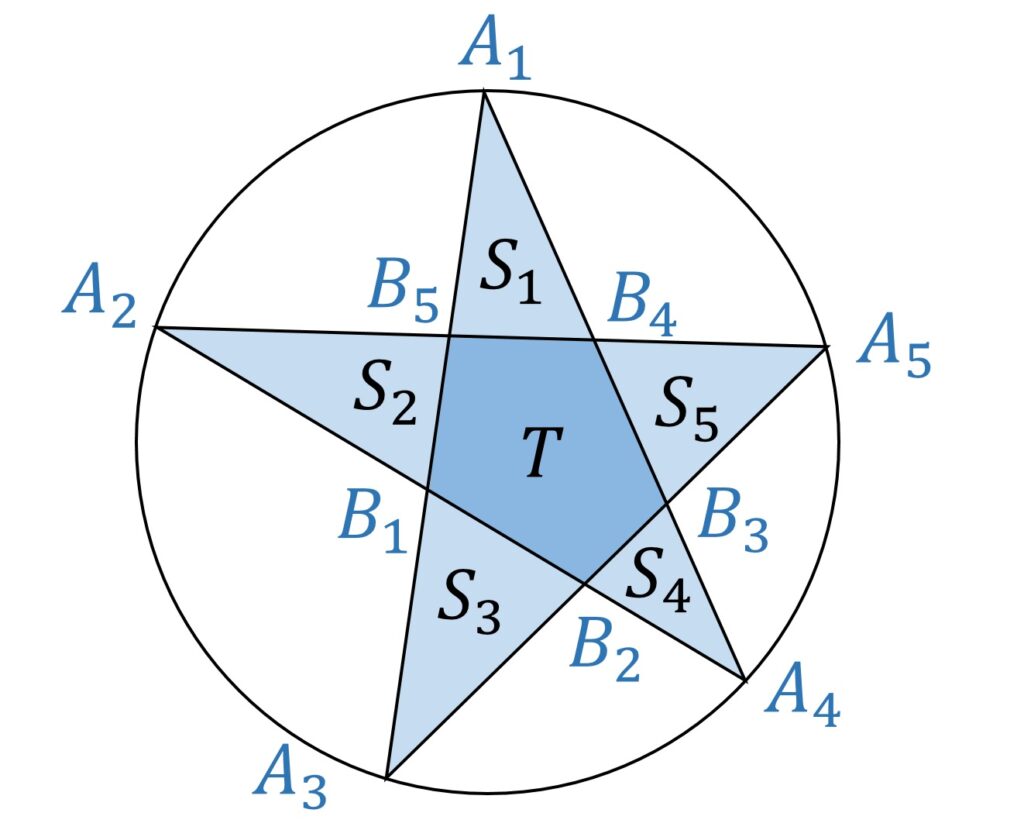
単に五芒星の面積を求めるのではなく、中央の五角形の面積が2倍なのが謎ですが、とりあえず見ていきましょう。
