東大– category –
-

一般項を導出できない数列の極限 – 2006年東大 数学 第5問
2006年東大 数学 第5問は数列の問題ですが、漸化式が線形ではなく、一般項を容易に求められないにもかかわらず、極限値を聞いてくるという、嫌げな問題です。問題文は以下の通りです。 とし、数列 を漸化式 によって定める。このとき、以下の問いに答えよ... -

複素平面上の図形問題 – 2000年東大 数学 第2問
2000年東大 数学 第2問 は、ミレニアムの年に東大が贈る複素数の問題です。複素平面に図形を絡ませてきています。問題文は以下の通りです。 複素数平面上の原点以外の相異なる2点 を考える。 を通る直線を 、原点から に引いた垂線と の交点を とす... -

死角なき難問 – 1996年東大 数学 第3問
1996年東大 数学 第3問 は、球と立方体に関する図形の問題です。問題文は以下の通りです。 空間内の点 O を中心とする1辺の長さが l の立方体の頂点を A1,A2, … ,A8 とする。また、 O を中心とする半径 r の球面を S とする。(1) S 上のすべての点から A... -

フィボナッチがこんなところまで! – 1998年東大 数学 前期 第3問
1998年東大 数学 前期 第3問は、平面図形と数列の問題です。これは解法の先取りというか、ネタバレですが、解いていくうちにフィボナッチ数列が、思いがけず現れてきます。 問題文は以下の通りです。 平面に2つの円 をとり、 を 軸と 、 に接する円と... -

ネイピア数の定義を再確認する – 2016年東大 数学 第1問
2016年東大 数学 第1問 は、いわゆる「ネイピア数」に関する問題です。 ネイピア数とは自然対数の底のことですが、学校ではこの名称で習わなかったため、今一つなじみがありません。ティッシュペーパー?、とか、西洋剣のレイピア?、とか、ボケをかま... -
逆関数の積分 – 2006年東大 数学 第6問
今回取り上げる、 2006年東大 数学 第6問 は、逆関数の積分に関する問題です。逆関数の積分などと突然言われるとギョッとしますが、慌てなくて大丈夫です。 問題文は以下の通りです。 を定義域とする関数 について、以下の問いに答えよ。(1) 関数 ... -

八面体 Strikes Back – 2019年東大 数学 第3問
2019年東大 数学 第3問 は、八面体に関する問題です。前回の出題から11年、何度も姿を現すその様は、ティアマト彗星のようです(遭遇周期は必ずしも一定ではありませんが)。 問題文は以下の通りです。 座標空間内に5点 、 、 、 、 を考える。線分 の中... -

複素平面上のフィボナッチ数列 – 2001年東大 数学 第4問
2001年東大 数学 第4問 は複素平面上の数列問題です。この分野は入試ではポピュラーなので、本番に備えて十分な準備をしておきたいものです。 本問の大きな特徴は、あのフィボナッチ数列 を複素数に適用しているところです。どんな興味深い結果が得ら... -
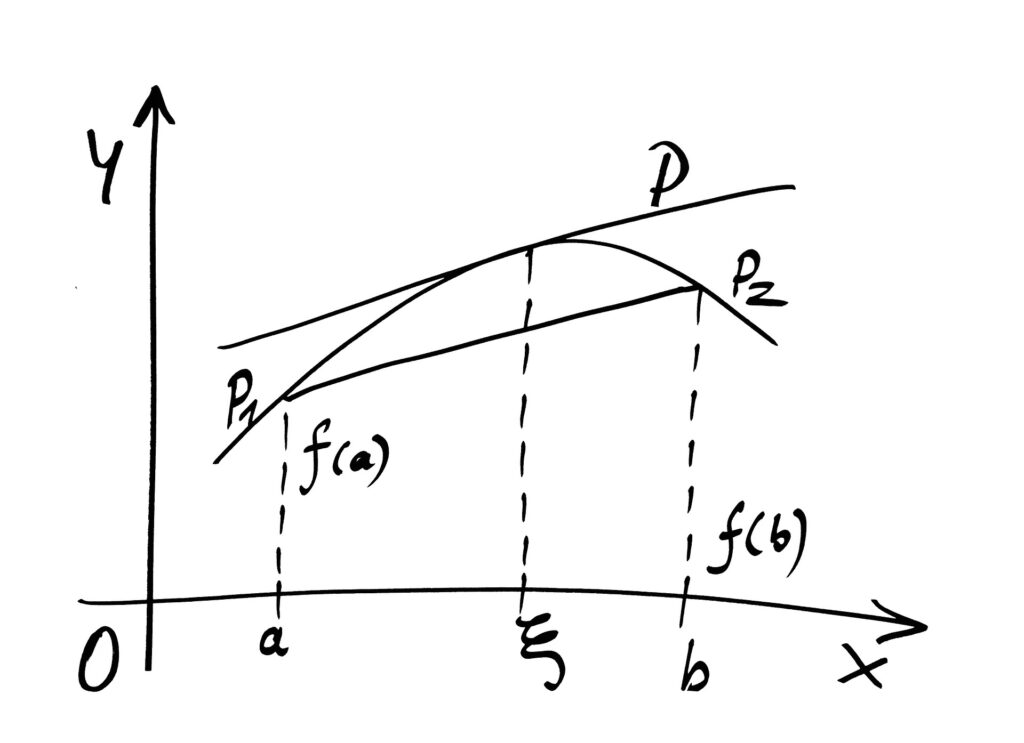
3次関数とガウス記号 – 1998年東大 数学 第4問
1998年東大 数学 第4問 は、後期試験にあの伝説の超難問が出題された年の問題で、3次関数にガウス記号を組み合わせるという、食い合わせの悪さが特徴の難問です。 問題文は以下の通りです。 実数 に対して をみたす整数 を であらわす。 を整数とし... -
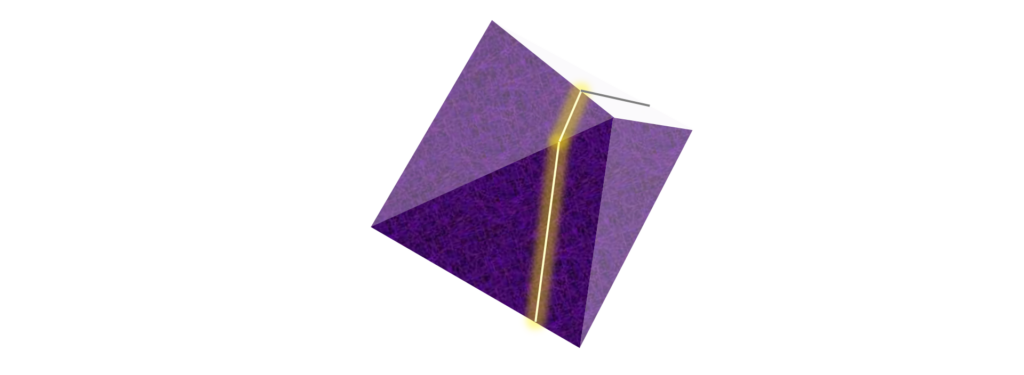
正八面体リターンズ – 2008年東大 数学 第3問
今回取り上げる 2008年東大 数学 第3問 は、正八面体の問題です。 以前の記事で、正八面体を扱った問題を紹介しました(1990年前期 第3問)。その年に生まれた人が受験期を迎えた正にその年、あの正八面体の脅威が、再び人類(の中の東大受験者)を...