今回は、3元連立方程式の問題を取り上げます。只の連立方程式ではありません。2次方程式で、しかも変数が循環しています。これは、 1997年京大 後期 数学 第4問 (理系)です。
1997年京大 後期 数学 第4問 とは
問題文は以下の通りです。
次の連立方程式 (*) を考える。
(*) \left \{
\begin{aligned}
& y= 2x^2 - 1 \\
& z=2y^2-1 \\
& x=2z^2-1
\end{aligned}
\right.
(1) (x,y,z)=(a,b,c) が (*) の実数解であるとき、 |a| \leqq 1 , |b| \leqq 1 ,|c| \leqq 1 を示せ。
(2) (*) は全部で8組の相違なる実数解をもつことを示せ。
ご覧の通り、連立方程式なのに2次で、しかも変数がぐるりと循環しています。
この手の問題の解法としては、普通は代入法によって変数を一つにし、微分したりして解の個数を評価しますが、この問題では出来上がる式が8次になってしまい、セオリー通りに進めても答えが出るのかもしれませんが、筆者は1階微分をやったところでくじけました。
そもそも、スタイリッシュな設問で知られる天下の京大が、べたべたと泥臭く計算させるような問題を出すはずがありません。実際、京大生が選ぶ感動した一問(数学・物理・化学) > 第1回 京都大学 1997年 数学(理系)・後期というページに、素晴らしく洗練された解答が載っています。
小問1の解法
先のリンク先に載っていますが、背理法を使って解くのが簡単で分かりやすいと思います。
仮に、|x| > 1 であるとします。すると、
\begin{aligned}
& y-|x| \\
& = 2x^2 - |x| -1 \\
& =(2|x|+1)(|x|-1) > 0
\end{aligned}であることから、 y > |x| が成り立ちます。同様に、z > y および x > z が成り立つことから、 x > |x| が成り立つことになりますが、これは矛盾なので、 |x| \leqq 1 であることが示せました。同様に、 |y| \leqq 1 および|z| \leqq 1 が成り立ちます。
小問2の解法
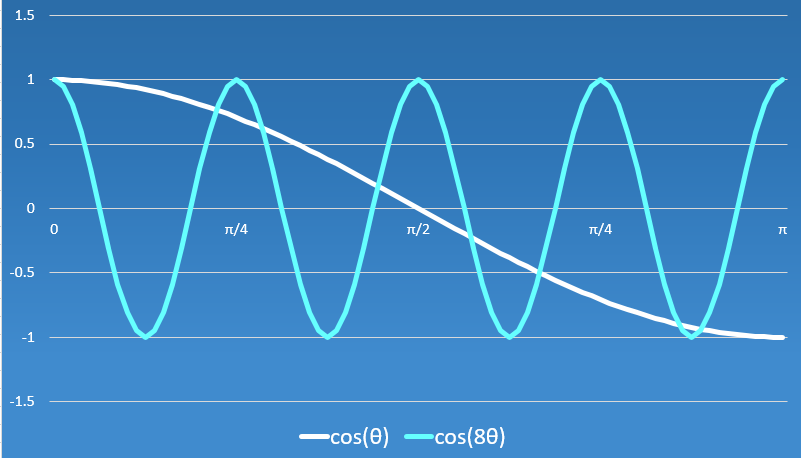
先のリンク先では、三角関数の2倍角の公式を適用する、という、実に鮮やかな手法で証明しています。元の連立方程式 (*) の y=2x^2-1 が、2倍角の公式に似ていることと、 |x| \leqq 1 であるところから、x=\cos \theta と置くと、元の連立方程式 (*) は、以下のような \theta の方程式に変形できます。
\left \{ \begin{aligned}
& \cos 2\theta= 2 \cos ^2 \theta - 1 \\
& \cos 4\theta= 2 \cos ^2 2 \theta - 1 \\
& \cos \theta= 2 \cos ^2 4 \theta - 1
\end{aligned}
\right.これと、 \cos 8\theta = 2\cos^2 4\theta -1 であることから、
\cos \theta = \cos 8 \theta
が得られます。べき乗項だけでなく、定数項もきれいになくなっているところが、正に驚きです。ここから \theta の、それぞれ異なる具体的な値を8個求められるので、題意は証明できました。
1997年京大 後期 数学 第4問 の対称式を用いた証明
誠に見事な証明ですが、仮に元の方程式が
\left \{ \begin{aligned}
& y= x^2 - 2 \\
& z=y^2-2 \\
& x=z^2-2
\end{aligned}
\right. であったとすると、これほど簡単には証明できないでしょう。そこで本稿では、変数が循環しているところに着目し、もう少し一般的な手法として、対称式を用いて証明してみます。
重根の確認
3つある式が同じ形であるところから、重根(と言ってよいのか、つまりは x=y=z である解)の存在が、十分に予想できます。実際、
x=2x^2-1
の2つの解から得られる (x,y,z)=(1,1,1) および (x,y,z)=(-\frac{1}{2},-\frac{1}{2},-\frac{1}{2}) は、確かに元の方程式の解になっています。
これで、8つの解のうち、2つの存在を証明することが出来ました。
対称式の具体的な値を求める
元の連立方程式 (*) を変形して、対称式の具体的な値を求めます。
xyz
まず、(*) の両辺から1を引きます。
\left \{ \begin{aligned}
& y-1= 2x^2 - 2 \\
& z-1=2y^2-2 \\
& x-1=2z^2-2
\end{aligned}
\right. 各式の両辺をすべて掛け合わせて、
(x-1)(y-1)(x-1)=8(x-1)(x+1)(y-1)(y+1)(z-1)(z+1)
を得ますが、 x=y=z=1 でない解を探すのであるから、両辺を (x-1)(y-1)(x-1) で割ることが出来て、
(x+1)(y+1)(z+1) = \frac{1}{8} \text{ } \cdots (1)を得ます。
次に、 (*) の両辺に1を足します。
\left \{ \begin{aligned}
& y+1= 2x^2 \\
& z+1=2y^2\\
& x+1=2z^2
\end{aligned}
\right. 辺々掛け合わせて、以下を得ます。
\begin{aligned}
& (x+1)(y+1)(z+1)=8x^2y^2z^2 \\
& \text{ } \cdots (2)
\end{aligned}(1)と(2)から、 xyz の値が求められます。
xyz=\pm{\frac{1}{8}} \text{ } \cdots (3)x+y+z と xy+yz+xz
(*) を辺々足し合わせます。
\begin{aligned}
& x+y+z = 2(x^2+y^2+z^2)-3 \\
& \text{ } =2(x+y+z)^2 \\
& \text{ } -4(xy+yz+xz) -3 \\
& \text{ } \cdots (4)
\end{aligned}また、(1)の左辺を展開します。
\begin{aligned}
& xyz \\
& +xy+yz+xz \\
&+x+y+z+1=\frac{1}{8} \\
& \text{ } \cdot \cdot \cdot (5)
\end{aligned}(3)、(4)、(5)より、 x+y+z と xy+yz+xz に関する、連立方程式が得られます。
\begin{aligned}
\left \{
\begin{aligned}
&2(x+y+z)^2 \\
&-(x+y+z) \\
& - 4(xy+yz+xz)-3=0 \\
\\
&(x+y+z) \\
& +(xy+yz+xz)+\frac{7}{8} \pm{\frac{1}{8}} = 0 \\
\end{aligned}
\right.
\\
\\
\text{ } \cdot \cdot \cdot (6)
\end{aligned}
(6)を解いて、x+y+z と xy+yz+xz の値を求めると、以下の表1のように、4種類の値を得ることが出来ます。
| 対称式 | 値1 | 値2 | 値3 | 値4 |
|---|---|---|---|---|
| x+y+z | –\frac{1}{2} | -1 | 0 | –\frac{3}{2} |
| xy+yz+xz | –\frac{1}{2} | 0 | –\frac{3}{4} | \frac{3}{4} |
| xyz | \frac{1}{8} | \frac{1}{8} | –\frac{1}{8} | –\frac{1}{8} |
実数解存在の必要条件証明
(*) の解 (x,y,z) が存在すれば、それは表1の4種類の値から得られる、以下の方程式群の解なので、これらの方程式が1でも -\frac{1}{2} でもない6個の異なる実数根を、 |x| \leqq 1 の範囲に持つことを証明します。
\begin{aligned}
& f_1(x) = x^3 + \frac{1}{2} x^2 - \frac{1}{2} x - \frac{1}{8} = 0 \\
& f_2(x) = x^3 + x^2 - \frac{1}{8} = 0 \\
& f_3(x) = x^3 - \frac{3}{4} x + \frac{1}{8} = 0 \\
& f_4(x) = x^3 + \frac{3}{2} x^2 + \frac{3}{4} x+ \frac{1}{8} = 0
\end{aligned}期待する実数解の数が6個なのに、3次方程式が4本もあるのはどうよ、とも思いますが、一つ一つ見ていきます。
まず、 f_1(x)=0 です。 f_1(x) の導関数を求めることにより、 f_1(x) が |x| \leqq 1 の範囲に極値を持ち、しかも f_1(-1) < 0, f_1(-\frac{1}{2}) > 0, f_1(0) < 0, f_1(1) > 0 であることから、 f_1(x)=0 が |x| \leqq 1 の範囲に3つの実数解をもつことがわかります。同様に f_3(x)=0 も、|x| \leqq 1 の範囲に3つの実数解をもつことが証明できます。
f_1(x)=0 と f_3(x)=0 が共通解を持たないことは、方程式 f_1(x) - f_3(x)=0 の解 -\frac{1}{2}, 1 が、f_1(x)=0 および f_3(x)=0 の解になっていないことから、示すことが出来ます。
一方 f_2(x)=0 ですが、 f_2(x) = (x+\frac{1}{2})(x^2+\frac{1}{2} x -\frac{1}{4}) と因数分解されます。3つの解のうちどれかが -\frac{1}{2} でかつ、他の解が -\frac{1}{2} ではない場合、その解のセットは方程式 (*) の解になりえないので、 f_2(x)=0 は対象外となります。
最後に、 f_4(x)=(x+\frac{1}{2})^3 なので、f_4(x)=0 も考慮から外します。
以上の考察により、6つの異なる実数の存在を示すことが出来ました。
十分条件の証明
これで終わったわけではありません。ここまでの論考により、方程式 (*) の実数解が存在すれば、それは f_1(x) = 0 または f_3(x) = 0 を満たすことは示せましたが、逆は必ずしも明らかではありません。
なぜそんなことになるかと言うと、対称式算出の際に実施した、方程式 (*) の辺々を足したり掛けたりする推論は、一般には逆方向には真ではないからです。
そこで、 f_1(x)=0 と f_3(x)=0 の解が (*) の解であることを、証明します。
証明の方針
まず、 f_1(x)=0 の3つの実数解を \alpha 、 \beta 、 \gamma と置く時、以下の等式が成立することを、証明します。
\begin{aligned}
\left \{
\begin{aligned}
& \alpha + \beta + \gamma = (2\alpha^2 - 1) \\
& \text{ } + (2\beta^2 -1) \\
& \text{ }+(2\gamma^2-1) \\
\\
& \alpha \beta + \alpha \gamma + \beta \gamma \\
& = (2\alpha^2 - 1) (2\beta^2 -1) \\
& + (2\alpha^2 - 1) (2\gamma^2-1) \\
&+ (2\beta^2 -1) (2\gamma^2-1)\\
\\
& \alpha \beta \gamma \\
&= (2\alpha^2 - 1) (2\beta^2 -1) (2\gamma^2-1)
\end{aligned}
\right. \\
\\
\cdot \cdot \cdot (7)
\end{aligned}(7)が証明できた時、 (2\alpha^2 - 1) 、 (2\beta^2 -1) 、 (2\gamma^2-1) はいずれも、 f_1(x)=0 の解となるので、それぞれ \alpha 、 \beta 、 \gamma のいずれかと等しくなります。
しかも、 \alpha 、 \beta 、 \gamma のいずれも、1および -\frac{1}{2} と等しくないので、 \alpha = (2\alpha^2 - 1) 、 \beta = (2\beta^2 - 1) 、 \gamma = (2\gamma^2 - 1) のいずれも成り立ちません。したがって、 \alpha 、 \beta 、 \gamma が (*) の解であることが示せます。
式(7)の証明
(7)の証明ですが、(7)の右辺を展開し、以下のように \alpha + \beta + \gamma 、 \alpha \beta + \alpha \gamma + \beta \gamma 、 \alpha \beta \gamma の合成に変形します。
\begin{aligned}
&(2\alpha^2 - 1) + (2\beta^2 -1) + (2\gamma^2-1) \\
&=2(\alpha^2+\beta^2+\gamma^2)-3 \\
&=2(\alpha+\beta+\gamma)^2 \\
& \text{ } -4(\alpha\beta+\alpha\gamma+\beta\gamma)-3
\end{aligned}\begin{aligned}
&(2\alpha^2 - 1) (2\beta^2 -1) \\
& \text{ }+ (2\alpha^2 - 1) (2\gamma^2-1) \\
& \text{ } + (2\beta^2 -1) (2\gamma^2-1) \\
&= 4(\alpha^2\beta^2 + \alpha^2\gamma^2 + \beta^2\gamma^2) \\
& \text{ } - 4(\alpha^2+\beta^2 +\gamma^2)+3 \\
&= 4(\alpha\beta+\alpha\gamma+\beta\gamma)^2 \\
& \text{ } - 8(\alpha^2\beta\gamma + \alpha\beta^2\gamma + \alpha\beta\gamma^2 ) \\
& \text{ } -4(\alpha^2 + \beta^2 + \gamma^2) + 3 \\
&=4(\alpha\beta+\alpha\gamma+\beta\gamma)^2 \\
& \text{ } -8\alpha\beta\gamma(\alpha + \beta + \gamma)\\
& \text{ } -4(\alpha+\beta+\gamma)^2 \\
& \text{ }+ 8(\alpha\beta+\alpha\gamma+\beta\gamma) \\
& \text{ } +3 \\
\end{aligned}\begin{aligned}
& (2\alpha^2 - 1) (2\beta^2 -1) (2\gamma^2-1) \\
&= 8\alpha^2\beta^2\gamma^2-4(\alpha^2\beta^2+\alpha^2\gamma^2+\beta^2\gamma^2) \\
& \text{ }+ 2(\alpha^2 + \beta^2 + \gamma^2) - 1 \\
&= 8\alpha^2\beta^2\gamma^2- 4(\alpha\beta+\alpha\gamma +\beta\gamma)^2 \\
& \text{ }+ 8\alpha\beta\gamma(\alpha + \beta + \gamma)\\
& \text{ }+ 2(\alpha+\beta+\gamma)^2 \\
& \text{ } - 4(\alpha\beta+\alpha\gamma+\beta\gamma) -1 \\
\end{aligned}変形のための計算量が思ったより多くて、ちょっと辟易しますが、これに表1の値を代入することで、(7)が成り立つことを示すことが出来ます。
f_3(x)=0 のほうも、同様の手順で証明します。
総括と今後の学習方針
変数が循環する連立方程式を解く場合、今回のように対称式を利用することは、有用ではあります。変数が3つの場合、3次方程式に帰着できるからです。しかし、対称式を導出するときに元の方程式の辺々を足したり、などという操作を行っている場合は、十分条件の証明が必要になりますので、注意が必要です。
対称式の導出が難しい場合もあります。いろいろ試して、簡単に対称式が得られない場合は、別のアプローチも考慮に入れたほうが良いでしょう。
本問の場合、対称式を使って解の存在を証明することはできましたが、思いのほか計算量が多くなりました。出題者の意図は、最初に引用した、あのカッコいい証明を思いつけ、と言うことなのかもしれません。本問を教訓に、もし2倍角公式や3倍角公式に似た方程式に出くわすようなことがあった場合は、三角関数に変数変換することも試してみてください。
対称式のハンドリングは基本動作なので、問題集もたくさんあります。パターンにはまれば簡単に解けることが多いので、問題をたくさん解いて、本番時に取りこぼすことのないようにしましょう。特に3項対称式は難易度が上がりますので、より重点的に取り組むようにしてください。
