小問1の解法
各平面 H_k , 1 \leqq k \leqq n に対し、その方程式を f_k(x,y,z) = a_k x + b_k y +c_k z +d_k = 0 と置きます。このとき、すべての (x,y,z) \in \mathbb{R}^3 に対し、 f_k(x,y,z) \leqq 0 か f_k(x,y,z) > 0 のいずれかなのだから、分割領域の個数はその組み合わせ個数である 2^n です。
というやり方では残念ながらダメですorz。たとえば n=3 で各平面 H_k , 1 \leqq k \leqq 3 が以下の通りであったとします。
\begin{aligned}
& H_1 : f_1(x,y,z)=x=0 \\
& H_2 : f_2(x,y,z)=y=0 \\
& H_3 : f_3(x,y,z)=z=0 \\
\end{aligned}このとき、平面 H_4 を f_4(x,y,z) = x + y + z -1 = 0 で定義すると、領域
\begin{aligned}
& \{ (x,y,z) \in \mathbb{R}^3 | f_1(x,y,z) \leqq 0 \text{かつ} \\
& \text{ } f_2(x,y,z) \leqq 0 \text{かつ} \\
& \text{ } f_3(x,y,z) \leqq 0 \}
\end{aligned}では、常に f_4(x,y,z) < 0 となります。
つまり、 f_k(x,y,z) の正負の任意の組み合わせは取りえないということですが、これは H_4 をどのように置いても、そうなってしまいそうです。
こういう時の常とう手段として、2次元で考えてみることにします。
平面上に、 n-1 本の平行でない直線が、どの3直線も1点で交わらないように引いてあったとします。そこに、どの直線とも平行でない直線を一本、既存の交点を通らないように追加します。
すると、その直線は必ず、他の直線と1つだけ交点を持ちます。交点が n -1 個なので、追加された直線は n 本の線分または半直線に分割されます。
それらの線分または半直線は、平面を分割してできた領域の1つに、それぞれ排他的に含まれ、しかもその領域を2つに分割します。すなわち、直線を追加することによって、領域は n 個増えます(図1)。
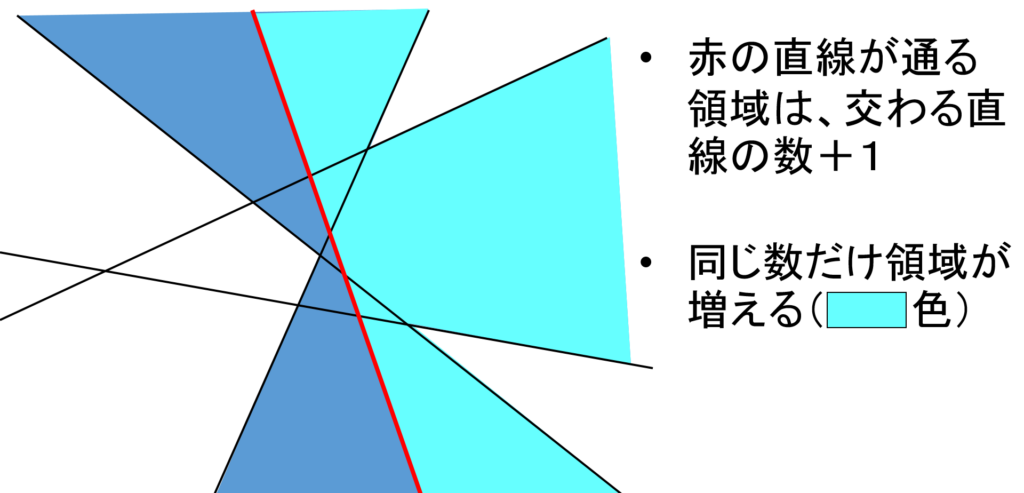
そこで、2次元平面を n 本の直線で分割したときの領域数の最大値を a_n とおくと、以下のような漸化式が成り立ちます。
\begin{aligned}
& a_1 = 2 \\
& a_{n} = a_{n-1}+ n & (n \geqq 2)
\end{aligned}一般項を求めると、
a_n = \frac{n(n+1) } {2} +1となります。
次に、この考え方を3次元に応用します。
空間が n 枚の互いに平行でない平面で分割されているとします。ここに、既存のどの平面とも平行でない新しい平面を追加します。
すると、その平面は、既存の n 枚の平面との交線である、 n 本の直線によって分割されます。
すべての平面が、たがいに平行でないので、追加の平面の法線ベクトルをうまく調整すれば、その平面を分割する各直線はお互いに平行でないようにすることが出来ます。
このとき、追加の平面は a_n 個の領域に分割されます。つまり、新しい平面が2分する領域が a_n 個あり、新たに増える領域も同じく a_n 個となります(図2)。
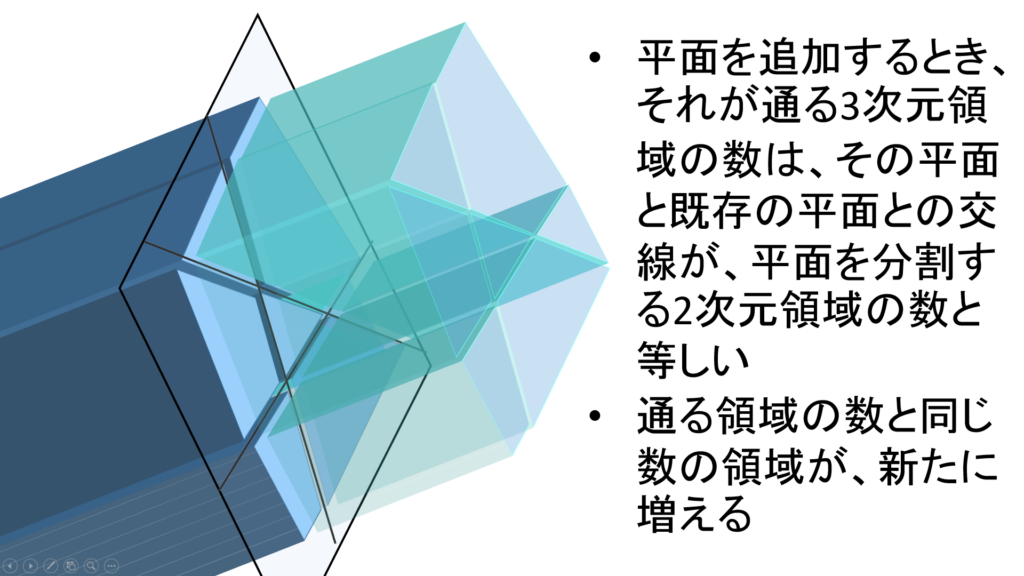
すなわち、 n 枚の平面で分割される領域数の最大値を b_n とおくとき、 b_n は以下の漸化式を満たします。
\begin{aligned}
& b_1 = 2 \\
& b_{n} = b_{n-1} + a_{n-1} & (n \geqq 2)
\end{aligned}一般項を求めると、
\begin{aligned}
& b_{n} - b_1 = \sum_{k=1}^{n-1} a_{k} \\
& = \sum_{k=1}^{n-1} \{ \frac{k(k+1)} {2} +1\} \\
& = \frac{(n-1)n(n+1) } {6} + (n-1) \\
& \therefore b_n = \frac{(n+1)(n^2-n+6) } {6}
\end{aligned}これが求める、空間分割数の最大値です。
小問2の解法
n=3 のときの、
\begin{aligned}
& H_1 : x=0 \\
& H_2 : y=0 \\
& H_3:x+y=1
\end{aligned}のケースがヒントになります。
H_1,H_2,H_3 はいずれも互いに平行ではありませんが、 H_3 を H_1 と H_2 の交線と平行になるようにすると、 H_1 と H_3 の交線と、 H_2 と H_3 の交線は平行になります(図3)。
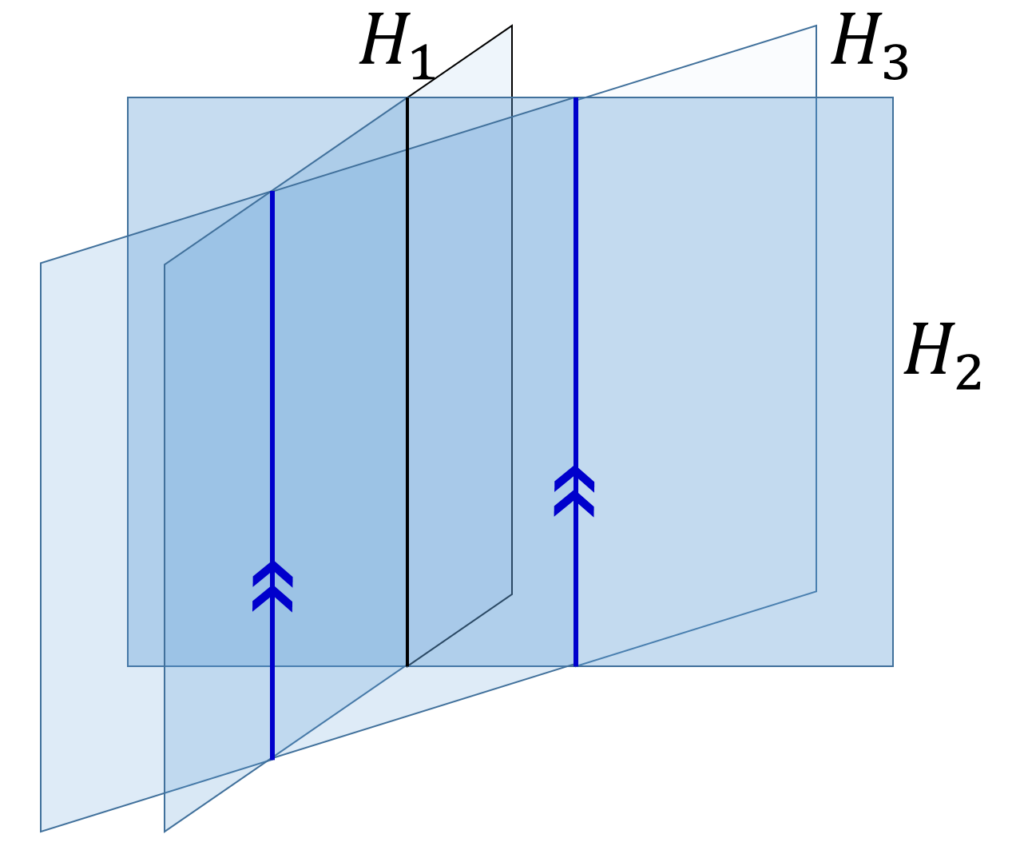
このとき、 H_3 は3つの2次元領域に分割されるので、 H_3 の追加によって新たにできる3次元領域は、3つです。もともと4つの領域があったので、合計領域数は7になります。最大値より1つ減りました。
この考え方を応用します。空間が n 枚の互いに平行でない平面で分割されているとき、新しい平面を、任意に選んだ既存の2平面の交線に平行になるように追加します。すると、それらの平面と新しい平面の交線のみが平行になり、平面の分割数は1つ減って a_n -1 となります。
したがって、 n 枚の平面で分割される領域数のうち、2番目に多い数を c_n とおくとき、 c_n は以下の式を満たします。
\begin{aligned}
& c_2 = 3 \\
& c_{n} = b_{n-1}+a_{n-1} -1 \\
& \text{ } = b_n -1
\end{aligned}ゆえに
\begin{aligned}
& c_{n} = \frac{(n+1)(n^2-n+6) } {6} - 1 \\
& \text{ } = \frac{n(n^2+5) } {6}
\end{aligned}となります。