死角なき難問 – 1996年東大 数学 第3問

　1996年東大 数学 第3問 は、球と立方体に関する図形の問題です。問題文は以下の通りです。

空間内の点 O を中心とする1辺の長さが l の立方体の頂点を A₁,A₂, … ,A₈ とする。また、 O を中心とする半径 r の球面を S とする。

(1) S 上のすべての点から A₁,A₂, … ,A₈ のうち少なくとも1点が見えるための必要十分条件を l と r で表せ。

(2) S 上のすべての点から A₁,A₂, … ,A₈ のうち少なくとも2点が見えるための必要十分条件を l と r で表せ。

　ただし、 S 上の点 P から A_k が見えるとは、 A_k が S の外側にあり、線分 PA_k と S との共通点が P のみであることとする。

　球面上のどの点からも、立方体の頂点が見えるようにするための条件を問われています。地表でGPS信号を常につかめるようにするにはどうすればよいか、と言う内容です。

　視点を頂点側に変えると、問題の主旨は球面上のすべての点が、頂点のどれかから常に見えるようにするということで、例えるならば、反射衛星砲の死角が無くなるように、8個の衛星を立方体状に配置せよ、と言った感じです。

小問１の解法

l < 2r の場合

　 l が十分に大きければ死角がなくなるというのは、直感的に明らかなので、死角が出来るぎりぎりのしきい値を探ることになります。

　まず、立方体が球にめり込んでいる場合（ l < 2r ）です。この場合明らかに、すべての頂点が地平線すなわち接平面の下にある地点が存在します(図1)。そのような地点ではどの頂点も見通すことはできません。

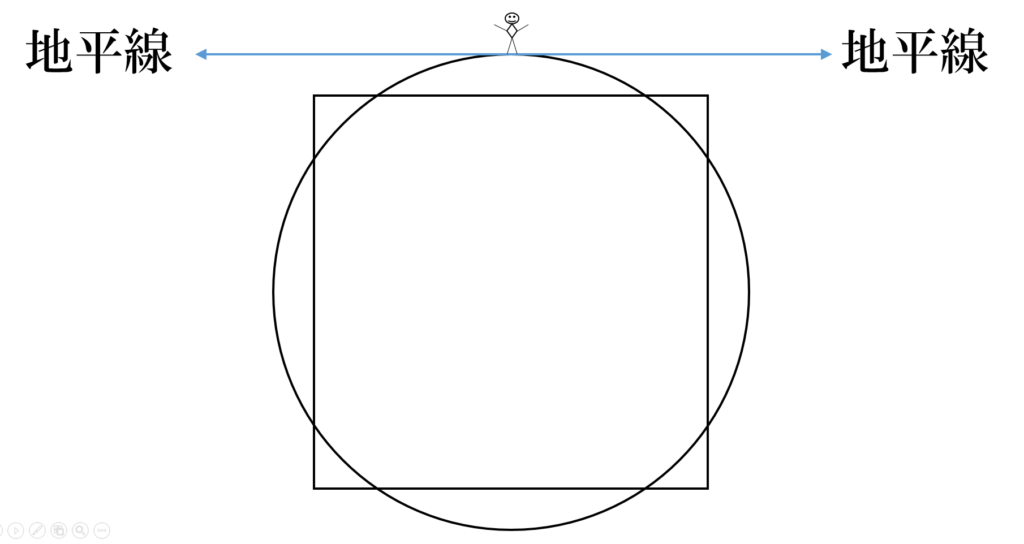
　したがって、S 上のすべての点から A₁,A₂, … ,A₈ のうち少なくとも1点が見えるための必要条件は、 l ≧ 2r です。