2007年東大 数学 第6問 は、自然対数の値を上下から評価する問題です。問題文は以下の通りです。
以下の問いに答えよ。
(1) 0 < x < a を満たす実数 x, a に対し、次を示せ。
\frac{2x}{a} < \int_{a-x}^{a+x} \frac{1}{t}dt < x ( \frac{1}{a+x} + \frac{1}{a-x} )
(2) (1) を利用して、次を示せ。
0.68 < \log 2 < 0.71
ただし、 \log 2 は2の自然対数を表す。
問題文を読んだ感じでは、小問1の不等式を証明できれば何とかなりそうな気がします。
小問1の解法
不等式左側の証明
まず、不等式の左側に取り組みます。左辺の \frac{2x}{a} は当然のことながら、 \frac{x}{a} が2つあるという意味ですが、ここから、積分項も \int_{a-x}^a \frac{1}t dt と \int_{a}^{a+x} \frac{1}t dt の2つに分ければよいのでは、と思いつくことが第1歩です。
このインスピレーションをもとに、不等式を以下のように変形します。
\frac{x}{a} - \int_{a}^{a+a} \frac{1}{t} dt < \int_{a-x}^{a} \frac{1}{t} dt - \frac{x}{a}この不等式を積分挟み撃ちの観点からとらえると、不等式は図1の①の面積が、②の面積より大きいということを主張していることがわかりますが、これは y = \frac{1}x の性質から明らかです。
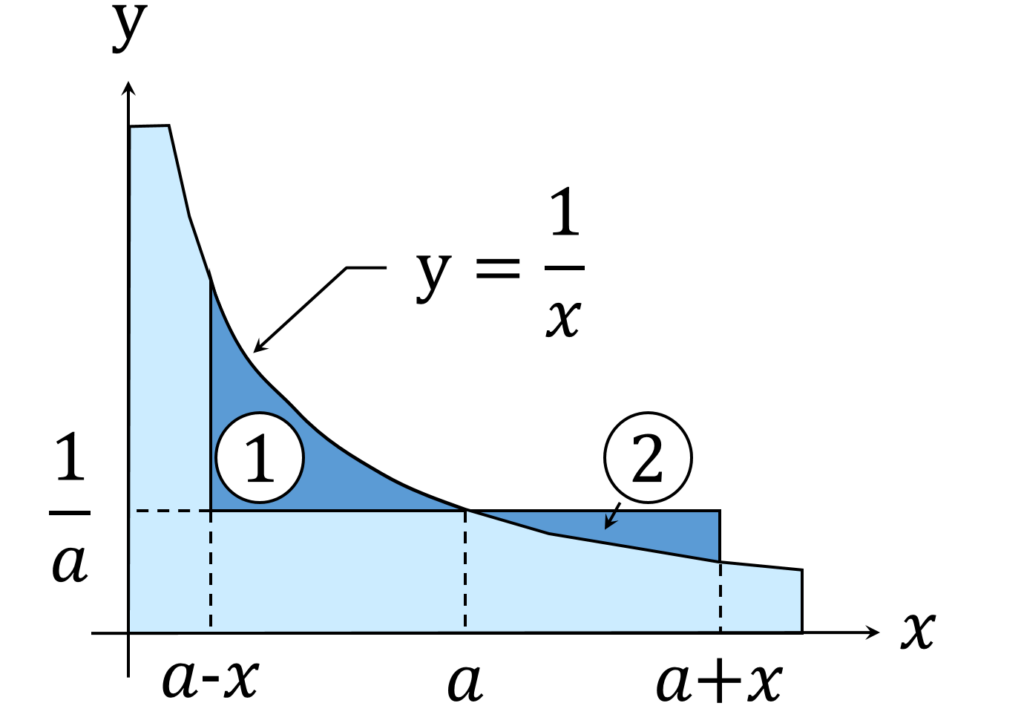
実際、 x = a を起点として、そこから等距離 r ( 0 < r < x ) の地点での \frac{1}{a-r} - \frac{1}{a} と \frac{1}{a} - \frac{1}{a+r} を比較すると、
\begin{aligned}
& \frac{1}{a-r} - \frac{1}{a} -\left (\frac{1}{a} - \frac{1}{a+r} \right ) \\
& = \frac{2a}{(a-r)(a+r)} - \frac{2}{a} \\
& = \frac{2\{a^2 -(a-r)(a+r) \} }{a(a-r)(a+r)} \\
& = \frac{2r^2 }{a(a-r)(a+r)} > 0 \\
\end{aligned}
となり、常に①側の被積分関数のほうが大きいことから、 ①の面積が②の面積より大きいことは明らかです。
まあ、試験本番で時間がないときには、図1を描いて「明らかである」と押し切ってもそこそこの部分点は期待できると思いますし、上記の理屈をつければ文句はないでしょうが、より数学っぽくまとめるのであれば、例えば以下のようにします。
積分範囲の中央を軸にグラフを反転させても積分値は等しいことから、
\int_{a}^{a+x} \frac{1}{t} dt = \int_{a}^{a+x} \frac{1}{2a + x -t} dt が成り立つことに注意すると、
\begin{aligned}
& \int_{a-x}^{a+x} \frac{1}{t} dt - \frac{2x}{a} \\
& = \int_{a-x}^{a} \frac{1}{t} dt + \int_{a}^{a+x} \frac{1}{t} dt - \frac{2x}{a} \\
& = \int_{a-x}^{a} \frac{1}{t} dt + \int_{a}^{a+x} \frac{1}{2a+x-t} dt - \frac{2x}{a} \\
& = \int_{a-x}^{a} \frac{1}{t} dt + \int_{a-x}^{a} \frac{1}{2a-s} ds - \frac{2x}{a} \\
& \text{ } (s=t-x\text{と変数変換} ) \\
& = \int_{a-x}^{a} \left ( \frac{1}{t} + \frac{1}{2a-t} -\frac{2}{a} \right ) dt \\
& = \int_{-x}^{0} \left ( \frac{1}{a+r} + \frac{1}{a-r} -\frac{2}{a} \right ) dr \\
& \text{ } (r=t-a\text{と変数変換} ) \\
& = \int_{-x}^{0} \frac{2r^2 }{a(a-r)(a+r)} dr > 0 \\
\end{aligned}以上、不等式の左側を証明することが出来ました。
不等式右側の証明
次に、不等式の右側に取り掛かります。
不等式左側の証明過程で
\begin{aligned}
& \int_{a-x}^{a+x} \frac{1}{t} dt - \frac{2x}{a} \\
&= \int_{-x}^{0} \left( \frac{1}{a+r} + \frac{1}{a-r} - \frac{2}{a}\right )dr \\
\end{aligned}という等式が現れましたが、これから導かれる等式
\begin{aligned}
& \int_{a-x}^{a+x} \frac{1}{t} dt
= \int_{-x}^{0} \left( \frac{1}{a+t} + \frac{1}{a-t} \right )dt \\
\end{aligned}を利用します。
f(t) = \frac{1}{a+t} + \frac{1}{a-t} と置く時、
\begin{aligned}
& f'(t) = - \frac{1}{(a+t)^2} + \frac{1}{(a-t)^2} \\
& \text{ } = \frac{4at}{(a+t)^2(a-t)^2}
\end{aligned}ですが、 -x <t< 0 の範囲で f'(t) < 0 です。したがって f(t) < f(-x) なので、
\begin{aligned}
& \int_{a-x}^{a+x} \frac{1}{t} dt \\
& = \int_{-x}^{0} \left( \frac{1}{a+t} + \frac{1}{a-t} \right )dt \\
& = \int_{-x}^{0} f(t)dt \\
& < \int_{-x}^{0} f(-x)dt \\
& = xf(-x) \\
& = x \left( \frac{1}{a-x} + \frac{1}{a+x} \right )
\end{aligned}が成り立ちます。
以上、不等式右側が証明できました。
小問2の解法
小問1の結果を使えと、問題文にはっきり書かれているので、当然それに従います。
であれば、不等式の真ん中の式を \log2 に対応させてみます。
真ん中の式 = \log 2 と置いてみる
とりあえず、
\int_{a-x}^{a+x} \frac{1}{t}dt = \log2を満たす a と x を求めます。
\log \left (\frac{a+x}{a-x} \right) =\log2なので
\frac{a+x}{a-x} =2です。これから、
x = \frac{1}{3}aを得ます。これを小問1の不等式に代入すると、
\frac{2}{3} < \log2 < \frac{3}{4}となります。求めたい不等式より緩い評価結果になっていますが、結構いい感じです。推論の方向はあっていそうです。
真ん中の式 = \log 2^n と置いてみる
それでは、真ん中の式を \log2^n ( n は2以上の整数)に対応させてみたらどうでしょうか。
\frac{a+x}{a-x} =2^nなので、
x = \frac{2^n - 1}{2^n+ 1}aとなり、
\frac{2(2^n-1)}{2^n+1} < \log2^n < \frac{2^{2n} - 1}{2^{n+1}}を得ます。両辺を n で割って、
\frac{1}{n} \left (\frac{2(2^n-1)}{2^n+1} \right )< \log2 < \frac{1}{n} \left (\frac{2^{2n} - 1}{2^{n+1}} \right )となりますが、 n を大きくすればするほど、評価は緩くなってしまいます。
真ん中の式 = \log \sqrt 2 と置いてみる
n を大きくするのがだめならば、小さくするのはどうか、というわけで、 真ん中の式を \log \sqrt 2 に対応させてみます。
\frac{a+x}{a-x} =\sqrt2なので、
x = (3 - 2\sqrt 2)a
となり、
2(3-2\sqrt 2) < \log \sqrt 2 < \frac{\sqrt 2}{4}を得ます。更に両辺に2を掛けて、
4(3-2\sqrt 2) < \log 2 < \frac{\sqrt 2}{2}ですが、「 \sqrt 2 = ひとよひとよにひとみごろ」なので、
\sqrt 2 < 1.42
です。このとき
4(3-2\sqrt2) >4(3-2 \times 1.42) = 0.64
なので、 \sqrt 2 の近似精度を上げる必要があります。それでは、
\sqrt 2 < 1.415
ではどうでしょうか。
4(3-2\sqrt2) >4(3-2 \times 1.415) = 0.68
なので、今度はOKです。一方、
\frac{\sqrt2}{2} < \frac{1.415}{2} =0.7075<0.71なので、不等式の右側もOKです。以上、小問2が証明できました。
解法のポイントと今後の学習方針

小問1を解くためには、不等式中央の積分範囲を (a-x,a) と (a,a+x) の2つに分けることが重要です。これは本稿で示したように、不等式左側の項に2がかかっていることから積分を2つに分けることを思いつくか、または不等式右側の形から気付くこともできると思います。
いずれにしても、本問を積分挟み撃ち問題のバリエーションととらえれば、自然に思いつけるでしょう。
小問2については、難しいことを考えずに中央の式 =2のべき乗と置いてみると、本稿で示したように a と x の値が求められるので、それを小問1の不等号に代入してみれば、答えに到達できると思います。
その際注意すべきことは、 \sqrt 2 の精度をどれくらいにするかです。本問は意外なことに、小数点以下3桁までの精度を要求していたので、本稿に示したようにちょっと苦労しました。
筆者は楽をしようとして近似値を使用しましたが、もちろん
\begin{aligned}
& 0.68 < 4(3-2\sqrt2) \\
& \text{ } \Leftrightarrow \\
& 0.17 < 3-2\sqrt2 \\
& \text{ } \Leftrightarrow \\
& 2\sqrt2 < 2.83 \\
& \text{ } \Leftrightarrow \\
& \sqrt2 < 1.415 \\
& \text{ } \Leftrightarrow \\
&2 < 2.002225
\end{aligned}などと、中3っぽくきっちり攻めるのもありです。
今後の学習方針としては、積分挟み撃ち問題を多く解いて、感覚をつかんでおくとよいでしょう。
