2014年京大 数学 第4問 は、有理式の合成関数に関する問題です。問題文は以下の通りです。
実数の定数 a, b に対して、関数 f(x) を
f(x)= \frac{ax+b}{x^2+x+1}
で定める。すべての実数 x で不等式
f(x) \leqq f(x)^3 - 2f(x)^2+2
が成り立つような点 (a,b) の範囲を図示せよ。
有理式というだけでもおぞましいのに、それを3次式に代入して大小を評価するという、実に強烈な問題です。これはもう、京大は泥沼計算を出題しないだろうという、一縷の望みにすがるしかありません。
それでは早速見ていきましょう。
2014年京大 数学 第4問 の解法
有理式を不等式に代入してみる
まずは有理式を不等式に代入してみます。これで何かわかるかもしれません。
\begin{aligned}
& \frac{ax+b}{x^2+x+1} \\
& \leqq \frac{(ax+b)^3}{(x^2+x+1)^3} - \frac{2(ax+b)^2}{(x^2+x+1)^2} \\
& +2
\end{aligned}これは通分する気も起きません。無理やり通分して分母を払っても、6次の不等式になって収拾がつかなくなりそうです。このアプローチはだめだと、早々に見切りをつけます。
不等式を f(x) の式ととらえて条件を抽出する
不等式に有理式を代入するのは筋が悪そうなので、不等式を f(x) の不等式、すなわち3次不等式ととらえて、成立条件を考えます。すなわち、
y \leqq y^3 -2y^2 +2\cdots(1)
が成り立つ実数 y の範囲を導き出し、 f(x) がすべての x に対してその条件を満たすような (a,b) の範囲を求める、というように2段構えにすれば、計算量が大幅に削減できそうです。
そこで、実数 y の関数 g(y) を
g(y) = y^3 -2y^2 + 2 -y
と定義します。このとき
g(y) = (y+1)(y-1)(y-2)
とたちどころに因数分解できるので、不等式(2)が成り立つ、すなわち g(y) \geqq 0 である必要十分条件は、
-1 \leqq y \leqq 1 \text{ または } 2 \leqq yとなります。条件が随分とすっきりしました。
すべての x に対して -1 \leqq f(x) \leqq 1 が成り立つための条件
すべての x に対して -1 \leqq f(x) \leqq 1 が成り立つための必要十分条件を、 a,b を使って表現します。
f(x) の最大値、最小値が1と-1の間に入っていれば良いのですから、まずは f(x) を微分して極値を求めます。おそらくそれらが最大値、最小値のはずなので、そこから a,b が満たすべき条件を導出します。
f(x) を微分した結果は以下の通りです。
\begin{aligned}
& f'(x) = \frac{a}{x^2+x+1} - \frac{(ax+b)(2x+1)}{(x^2+x+1)^2} \\
& = -\frac{ax^2+2bx-a+b}{(x^2+x+1)^2}
\end{aligned}f'(x) = 0 の解がすっきりした形に表現できないので、このまま進んでいっても泥沼に陥りそうです。
このアプローチも筋が悪そうなので、別の方法を模索します。
不等式 -1 \leqq f(x) \leqq 1 の分母を払ってみる
有理式のまま不等式を評価しようとしたので泥沼に落ちかけましたが、よく見ると f(x) の分母はすべての実数 x に対して常に正です。つまり、不等号の向きとか面倒くさいことを何も考えずに分母を払って、以下のように二次式の不等式に帰着できます。
\begin{aligned}
& -(x^2+x+1) \leqq ax+b & \cdots(2)\\
& \text{ かつ} \\
& ax+b \leqq x^2+x+1 &\cdots(3)
\end{aligned}2次式にしたおかげで、すべての x に対して不等式(2)および不等式(3)が成り立つ必要十分条件を、判別式で表現できます。
不等式(2)については、以下の通りです。不等式を変形して
x^2+(a+1)x+(b+1) \geqq 0
となりますが、これがすべての x に対して成り立つ必要十分条件は
(a+1)^2-4(b+1) \leqq 0
です。整理すると
b \geqq \frac{1}{4}(a+1)^2-1\cdots(4)を得ます。
不等式(3)も同様に変形して
x^2+(1-a)x+(1-b) \geqq 0
となりますが、これが すべての x に対して成り立つ必要十分条件は
(1-a)^2-4(1-b) \leqq 0
です。整理すると
b \leqq -\frac{1}{4}(a-1)^2+1\cdots(5)を得ます。
すべての x に対して 2 \leqq f(x) が成り立つための条件
すべての x に対して 2 \leqq f(x) が成り立つための必要十分条件は、 -1 \leqq f(x) \leqq 1 のときのように f(x) の分母を払って
2(x^2+x+1) \leqq ax+b
がすべての x に対して成り立つことで、この不等式を変形すると
2x^2+(2-a)x+2-b \leqq 0
ですが、 a,b をどのように選んでも上記の2次関数は下に凸であり、下に凸な二次関数は x の絶対値が十分に大きければ必ず正になります。すなわち、すべての x に対して 2 \leqq f(x) を満たすような a,b は存在しません。
結論
以上の考察より、すべての x に対して 問題文の与式が成り立つための必要十分条件は不等式(4)および不等式(5)が成り立つことで、このときの (a,b) の範囲を図示すると、以下の図1のようになります。
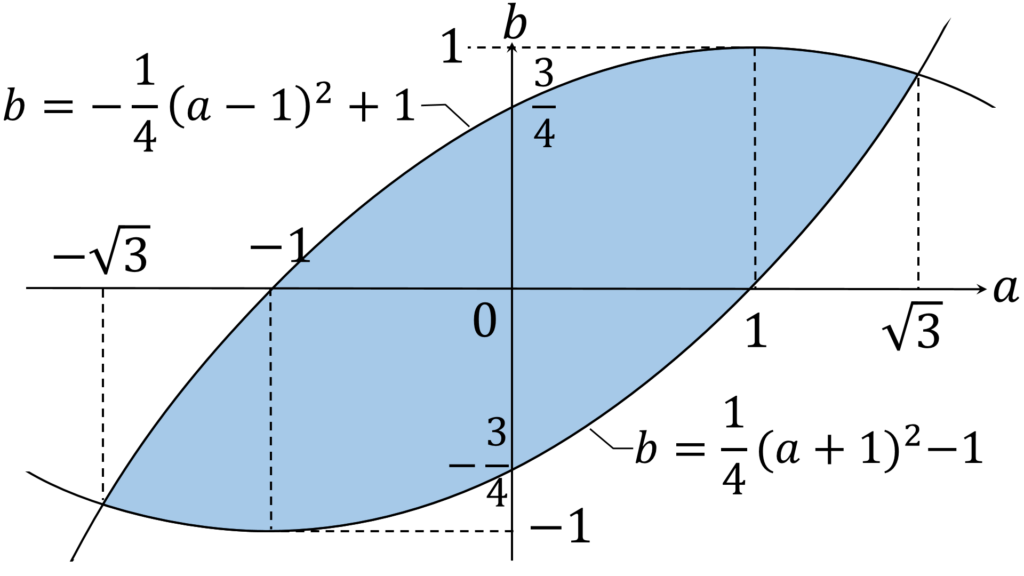
解法のポイント

京大の問題は、ツボにはまればすっきり解けることが多いと思います。
本問に関して言えば、与えられた不等式を x の式としてとらえるのではなく、 f(x) の式としてとらえることが最重要ポイントです。これに気が付くと、問題の見通しが俄然違います。
これをどうやって思いつくかですが、変数の次数をなるべく下げたい、下げるためにはどうすればいいかと考え続けることが一つの手法です。不等式が f(x) の3次不等式になっていることも、ヒントになります。
次に、 f(x) の範囲が絞られてきたときに、これを x の二次不等式に変形して判別式の正負に帰着させることです。 f(x) の範囲が与えられたからと言って、 f(x) の最大値、最小値を求めようとするのは、特に本問のような有理式の場合には、本稿で示した通り上手くいきません。
有理式の極値を求めようとすると、大抵は計算が複雑になるので、出来れば分母を払って多項式の大小に帰着できないかとか、常に考えるようにするとよいでしょう。
