今回は趣向を変えて高校入試です。 2010年ラサール高校 数学 第6問 を取り上げます。問題文は以下の通りです。
図において、△ABCはAC=10、BC=4、∠ACB=90°の直角三角形で、△ABDはAD=BD、∠ADB=90°の直角二等辺三角形である。線分BDと線分ACの交点をE、直線ABと直線CDの交点をFとするとき、次の問いに答えよ。

(1) ADの長さを求めよ。
(2) 線分の長さの比 BE:ED を求めよ。
(3) 線分の長さの比 DC:CF を求めよ。
(4) △BCFの面積を求めよ。
ぱっと見、それほど難しくなさそうです。小問を順番に解いていきます。
小問1の解法
これは単純に、3平方の定理を使って計算するだけです。
まず、 AB の長さを求めます。
\begin{aligned}
& \mathrm{AB} = \sqrt{ \mathrm{AC}^2 + \mathrm{BC}^2} \\
& \text{ } = \sqrt{ 10^2 + 4^2} \\
& \text{ } = 2 \sqrt{29}
\end{aligned}次に、三平方の定理を △ABD に適用します。この3角形が二等辺三角形であることに注意すると、
\begin{aligned}
& \mathrm{AD} =\frac{1}{ \sqrt{2}} \mathrm{AB} \\
& \text{ } = \sqrt{ 58} \\
\end{aligned}となります。変な値なのがちょっと気になりますが、とりあえず先に進みます。
小問2の解法
まず、四角形 ABCD が、 AB を直径とする円に内接することに注意します。すると明らかに、△AED と △BEC は相似で相似比は \sqrt{58} :4 です。 BE:ED を求めたいので、
\begin{aligned}
& \mathrm{BE} = x \\
& \mathrm{AE} = y \\
\end{aligned}と置きます(図2)。
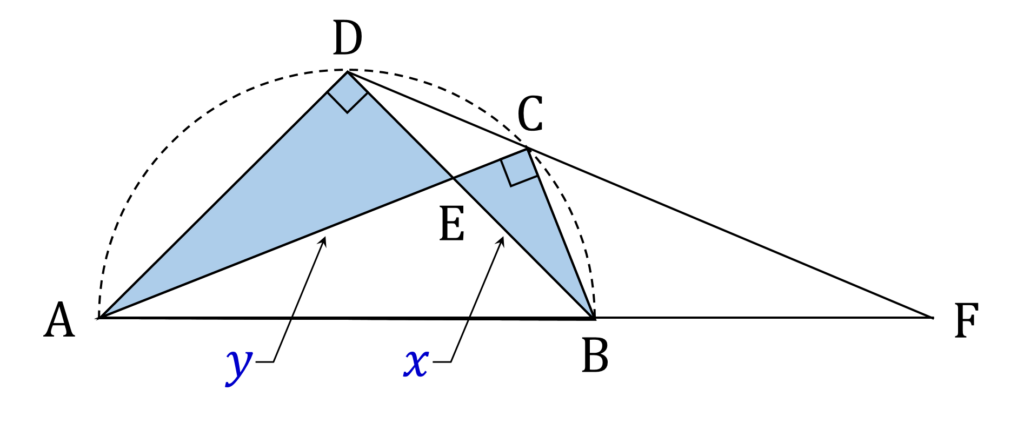
すると
\begin{aligned}
& \mathrm{ED} = \sqrt{58} -x \\
& \mathrm{EC} = 10- y \\
\end{aligned}なので
\begin{aligned}
y:x = \sqrt{58} -x :10- y = \sqrt{58} :4 \\
\end{aligned}が成り立ちます。
よって
\left \{ \begin{aligned}
& \sqrt{58} x = 4y \\
&4( \sqrt{58} -x) = \sqrt{58}(10-y) \\
\end{aligned}
\right .なので、これを解いて
\begin{aligned}
x & = \frac{4 \sqrt{58}}{7} \\
y &= \frac{58}7 \\
\end{aligned}を得ます。
ゆえに
\begin{aligned}
\mathrm{BE}:\mathrm{ED} & = x: \sqrt{58} -x \\
& = \frac{4 \sqrt{58}}{7} : \frac{3 \sqrt{58}}{7} \\
& = 4:3
\end{aligned}です。
小問3の解法
相似比を駆使してDCとCFの具体的な値が計算できそうなので、その方向で考えてみます。
まず DC ですが、小問2を解く過程で BE および ED の長さが具体的に得られているので、△EDC ∽ △EAB であることを利用します(図3)。
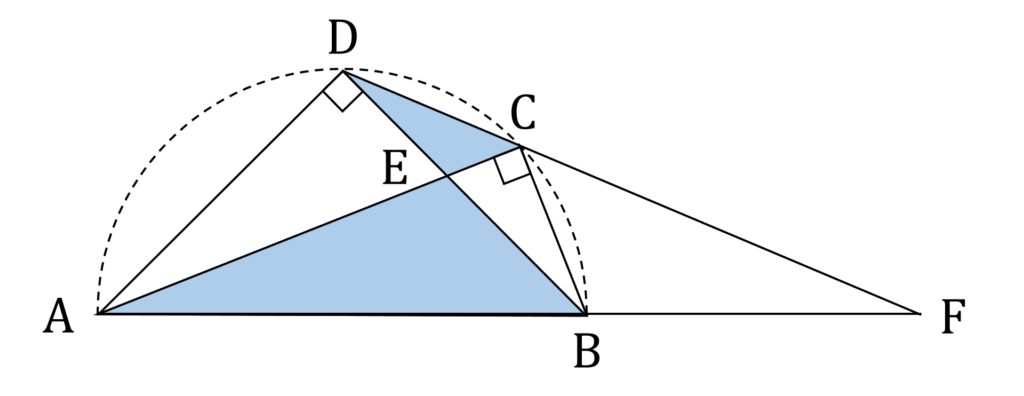
小問2で
\begin{aligned}
\mathrm{BE} & = \frac{4 \sqrt{58}}{7} \\
\mathrm{AE} &= \frac{58}7 \\
\end{aligned}であることがわかっているので、 △EDC と △EAB の相似比は
\begin{aligned}
& \mathrm{CE} : \mathrm{BE} \\
= & 10 - \mathrm{AE} : \mathrm{BE} \\
= &10- \frac{58}7 :\frac{4 \sqrt{58}}{7} \\
= & \frac{12}7 :\frac{4 \sqrt{58}}{7} \\
= &3: \sqrt{58} \\
\end{aligned}です。したがって
\mathrm{DC} = \frac{3}{\sqrt{58}} \mathrm{AB} = \frac{3}{\sqrt{58}} \times 2 \sqrt{29} = 3 \sqrt{2}です。
次に CF の長さですが、ここで △DCA ∽ △BCF であることに注意します。実際、 四角形 ABCD が円に内接するので、
∠ADC = ∠FBC
です。
また
∠DCA = ∠DBA = 45°
∠BCF = ∠DAB = 45°
なので
∠DCA = ∠BCF = 45°
が成り立ちます(図4)。
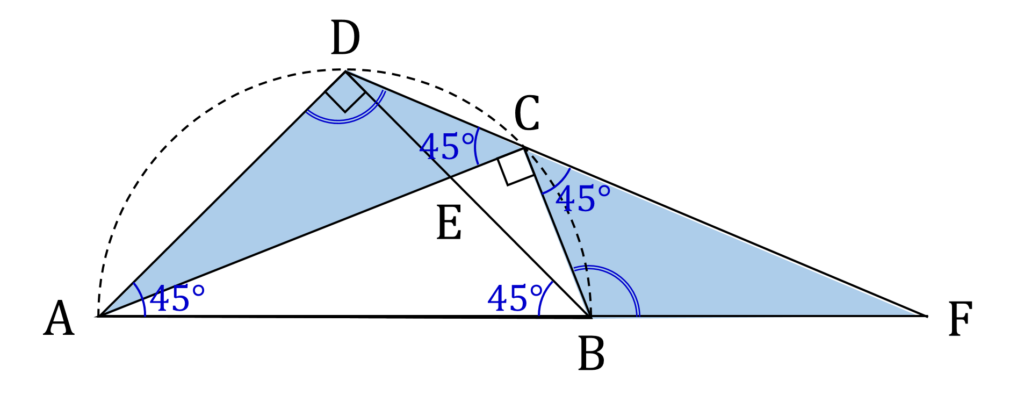
△DCA と △BCF の相似比は DC と BC の長さの比で、その値は
3\sqrt{2} :4です。したがって
\mathrm{CF} = \frac{4}{3 \sqrt{2}} \mathrm{CA} = \frac{20 \sqrt{2}}{3}であり、
\mathrm{DC}: \mathrm{CF} = 3 \sqrt{2} : \frac{20 \sqrt{2}}{3} = 9:20です。
小問4の解法
本問で面積がわかっている三角形は △ABC なので、これをうまく利用できないかと考えるうちに、 AB と BF の長さの比が △ABC と △BCF の面積比だと気が付ければ勝ちです(図5)。
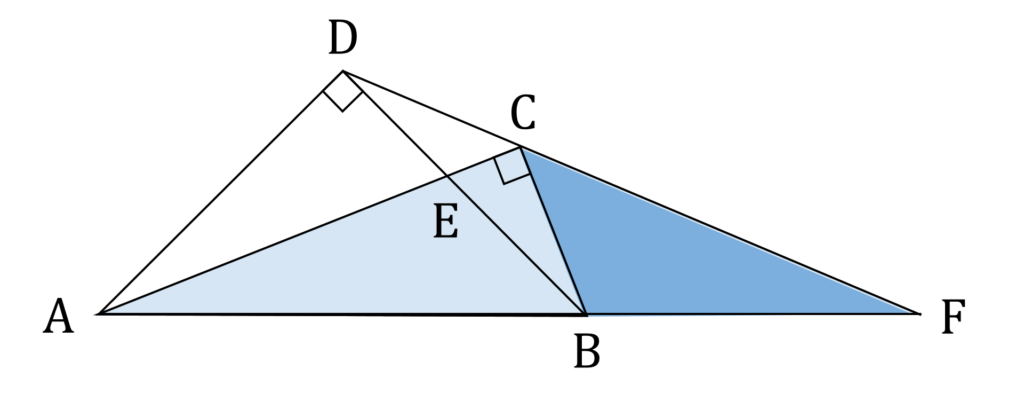
小問3で △DCA と △BCF の相似比は算出済みなので、 BF の長さはソッコーわかって
\mathrm{BF} = \frac{4}{3 \sqrt{2}} \mathrm{DA} = \frac{4 \sqrt{29}}{3}です。 \mathrm{AB} = 2 \sqrt{29} であったので、△BCFの面積は
20 \times \frac{4 \sqrt{29}}{3} \div 2 \sqrt{29} =\frac{40}3です。
解法のポイント

本問のように線分の長さや比を求める問題の場合、使用するツールは主に以下の通りです。
- 相似、合同
- 面積比
- 三平方の定理
また、小問2で見たように、図形が円に内接している場合は見逃さないようにしましょう。円周角などを使って相似関係を導くことが出来ます。
本問では出てきませんでしたが、何かに平行な補助線を引くというのも、重要な手法です。
難関校の図形の問題は、角度の関係性などをわかりにくくして難易度を挙げているので、これらの手法を積極的に試してみてください。
小問2のように、いろいろな辺の長さが絡むような場合には、登場するすべての量を躊躇せずどんどん変数に置いて、方程式を立ててみましょう。変数がたくさんあっても、あとで代入などで消せばよいのです。
辺の長さを求める問題では、代数的なアプローチも有効です。いろいろ悩む前に、まずは書き下してみましょう。
