2019年千葉県公立高 前期 数学 第4問 小問2 は図形の問題ですが、思いのほか難しく、舐めてた相手が実は殺人マシーンでした的な意表を突く問題です。
問題文は以下の通りです。
右の図のように、平行四辺形 ABCD があり、辺 AD 、 BC の中点をそれぞれ P,Q とする。2点 R,S を平行四辺形 ABCD の外側に、四角形 PRQS がひし形になるようにとる。線分 PQ と線分 RS の交点を E 、線分 RS と辺 CD の交点を F 、辺 CD と辺 PS の交点をGとする。
このとき、次の(1),(2)の問いに答えなさい。
(1) 略
(2) RQ=5cm ,AD=4cm ,PG=DG=3cm のとき、線分 FS の長さを求めなさい。
問題文の図は以下の通りです。
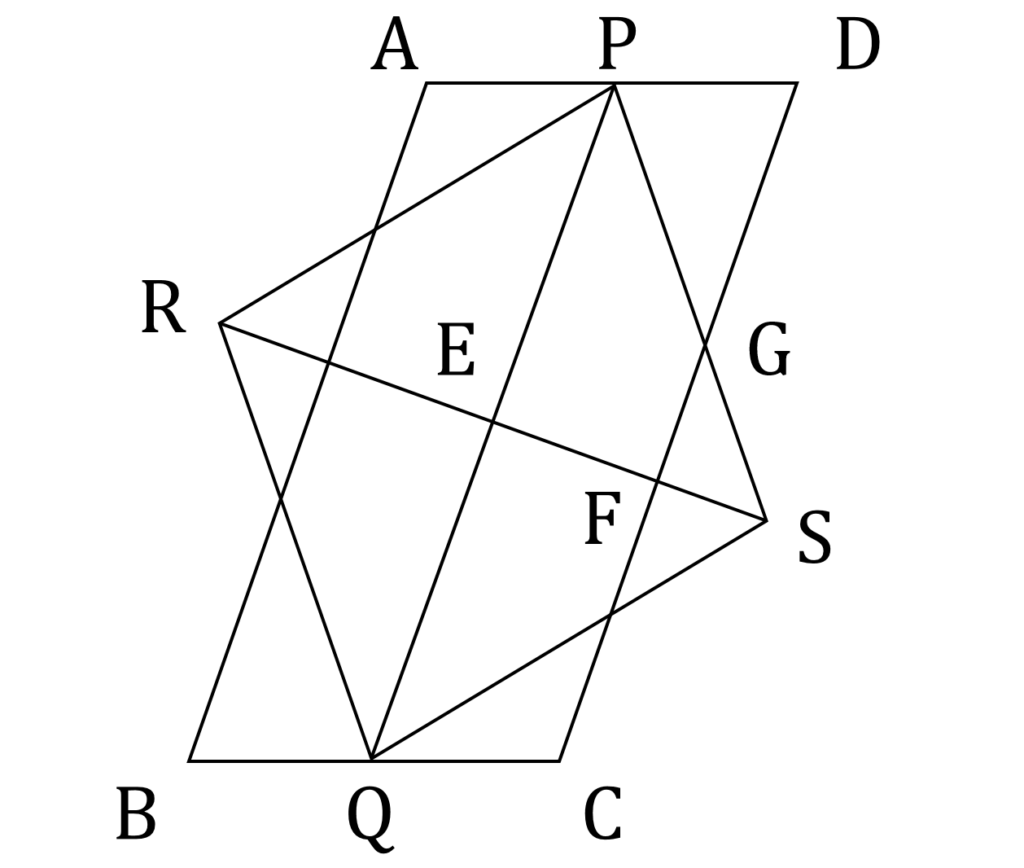
小問1は △RQE ∽ △SGF の証明の穴埋め問題で、教科書レベルのどうと言うことのない問題です。小問2も同じレベルかと思ったら、とんでもありませんでした。
小問2の解法
図に情報を書き込んでみる
まず、わかっている情報を図に書き込んでみます(図2)。
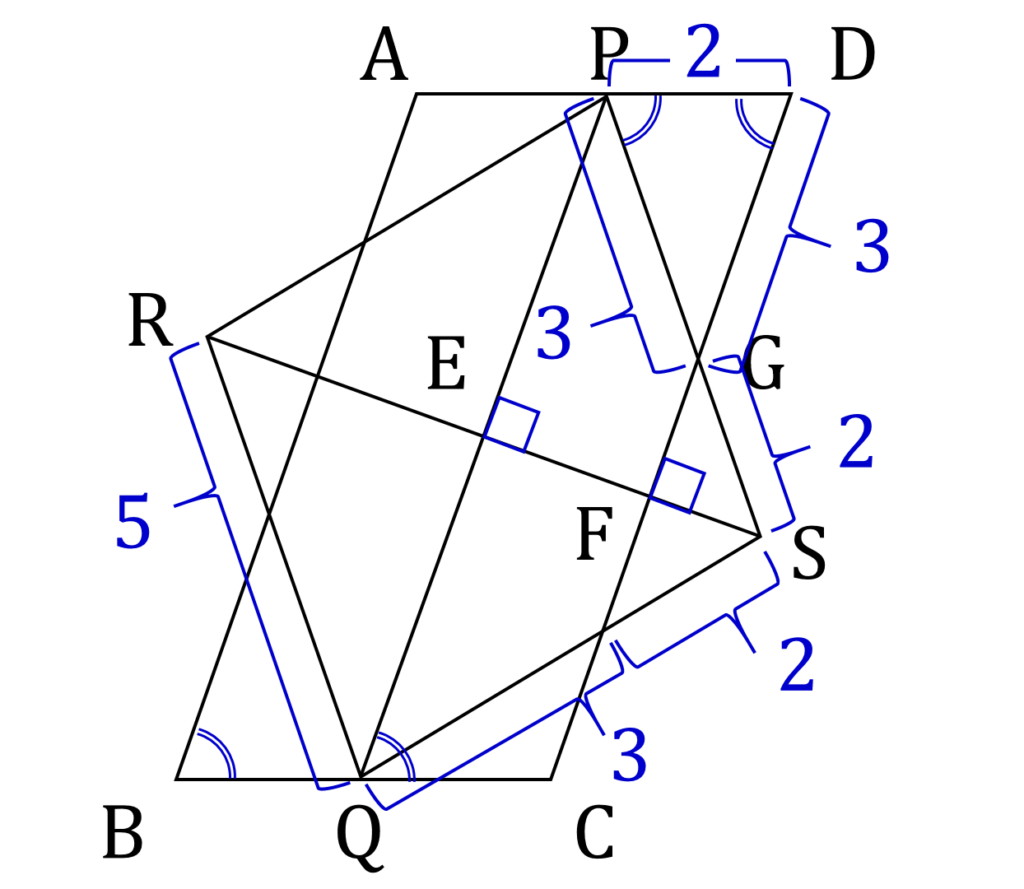
たくさん情報があるので、すぐにでも答えが出そうです。ひし形 PRQS の 対角線 PQ の長さが分かれば PE がその半分なので、3平方の定理から線分 ES の長さがわかって、三角形の相似比から ES:FS=5:2 が成り立つことから、答えは直ちに得られるのですが、実はこの図をにらんでいただけでは、 PQ の長さは得られません。このあたりから、思ったより難しい問題であることが明らかになってきます。
補助線を引く
ここで知恵を絞ります。 ひし形 PRQS の1辺の長さが5であるという条件だけでは、 PQ の長さは一意に決まりません。これが一意に定まるのは、 PG=DG=3 と言う条件があるからです。
この条件が答えを出すのに必須であることを念頭に、改めて図2を見ると、PG=3 と言う条件は GS の長さを出したり ES:FS の比を求めたりするのに使用していますが、せっかく ∠GPD が ∠GDP が等しくなっているのに、 ∠GPD と同位角や錯角の関係にある角度が、図2に現れていません。
そこでそのような角度が現れるように、補助線を引いてみます。辺 BC と辺 PS のそれぞれの延長線の交点をTとおきます。このとき ∠GPD=∠PTQ ですが、 ∠GDP=∠PQT であったので、 △GPD∽△PTQ が成り立ちます(図3)。
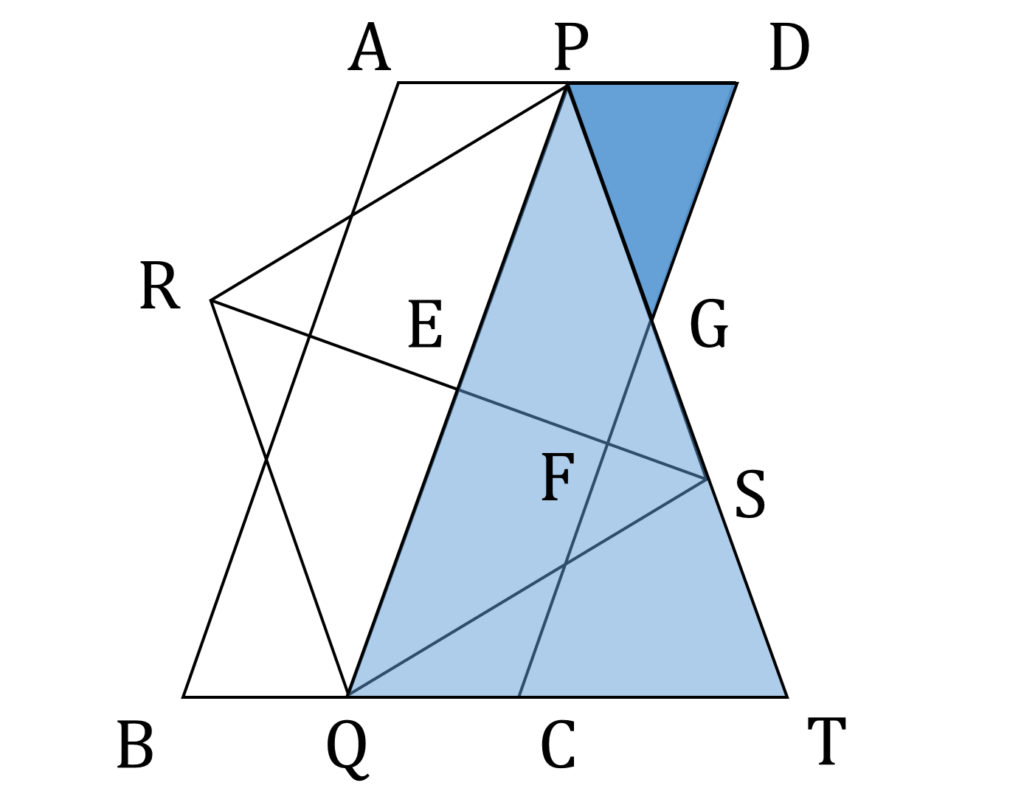
三角形の相似比が分かれば、 PQ の長さは一発で分かりますが、間抜けなことに肝心の相似比がわかりません。
相似比がわかる三角形を作り出す
それではということで、相似比がわかる三角形が出来るように、補助線を引きます。
PS の長さがわかっているので、これが1辺になるような三角形を作ります。 S を通り、 AD と平行な直線と PQ との交点を U と置きます。このとき、 △GPD∽△PSU であり、その相似比は 3:5 です(図4)。
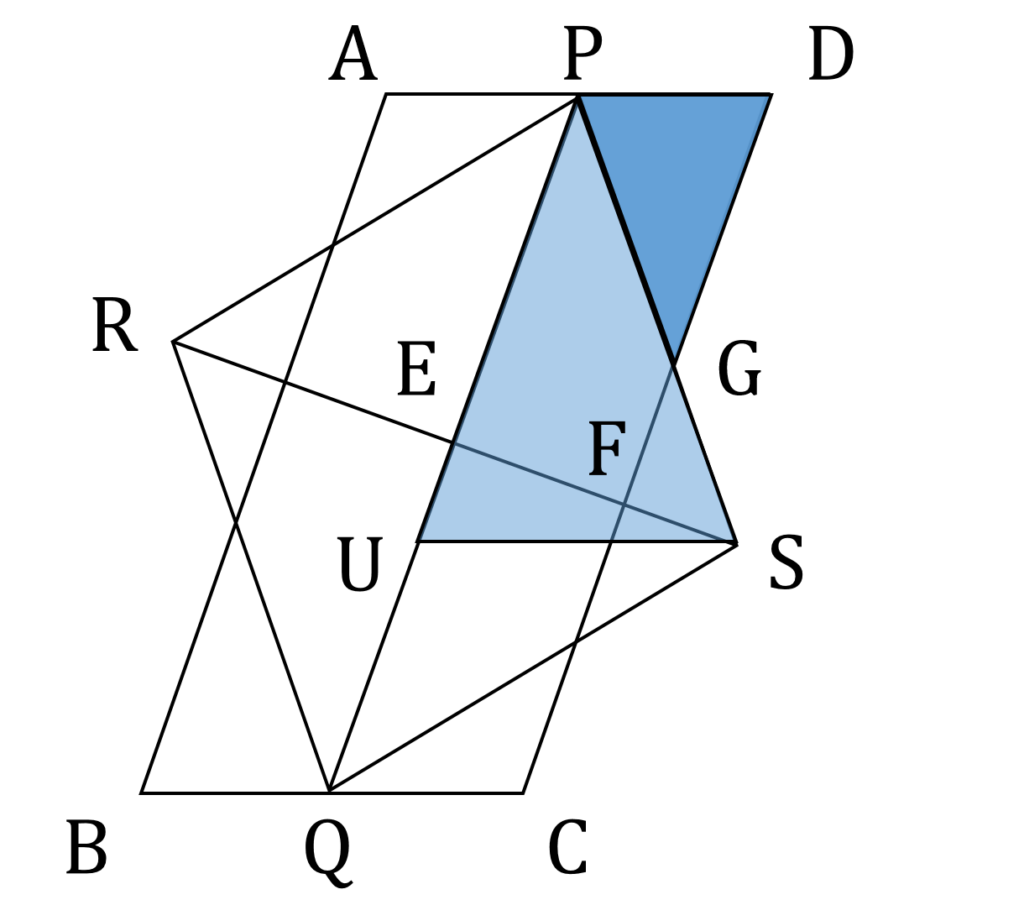
今度は相似比がわかっているので、USの長さが出ます。
\mathrm{US} = \frac{5}{3} \times2 = \frac{10}{3} ここでEUの長さが分かれば、PEの長さがわかってES、ひいてはFSの長さがわかります。 そこで
\begin{aligned}
& \mathrm{EU} = x \\
& \mathrm{ES} = y
\end{aligned}と置いて連立方程式
\left \{
\begin{aligned}
& x^2 + y^2 = \left(\frac{10}{3} \right)^2 \\
& (5-x)^2 + y^2 = 5^2
\end{aligned}
\right .を解いてもよいのですが、計算が面倒くさそうなので、もっと簡単に算出することを模索します。
△SUE と相似な三角形はどこかにないかと図4を見てみるに、 PD の中点を V と置いた時、 △GDU は △SUE といい感じに相似になります(図5)。
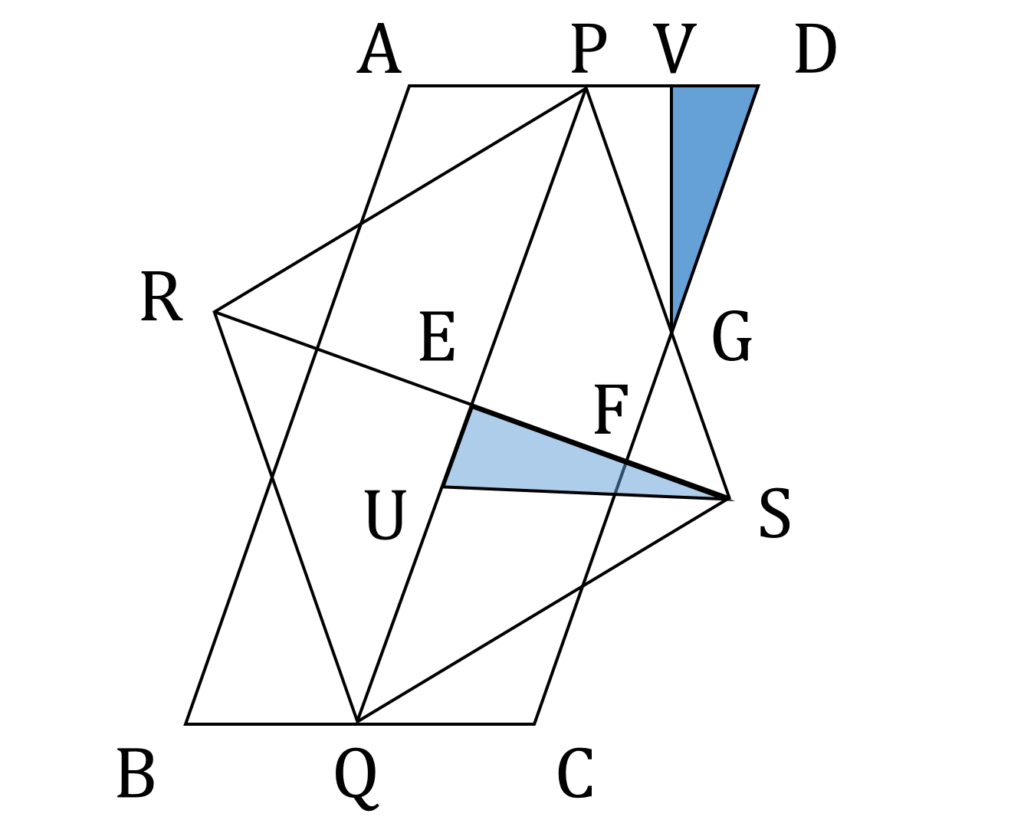
△GDU と △SUE の相似比は 3 : \frac{10}{3} =9:10 、また VG の長さが 2 \sqrt{2} (DG=3、VDはPDの半分なので1、よって三平方の定理から計算できる)なので、
\mathrm{ES} = 2\sqrt{2} \times \frac{10}{9} = \frac{20 \sqrt{2}}{9}ゆえに
\mathrm{FS} = \frac{2}{5}\mathrm{ES} = \frac{8 \sqrt{2}}{9} \mathrm{(cm)}です。
解法のポイント

本問は補助線の引き方をどうやって思いつくかがポイントです。線分の長さを出すには3平方の定理か相似比なので、相似な三角形をどう作るか、と言う観点で考えてみましょう。
また、本稿で示したように、使われていない条件があれば、それを活用できないかと言う観点で、補助線を引くことを考えてみましょう。
それにしても、本稿の内容を5分程度で考えなければならないのはなかなか厳しいものがあります。本問に限らず、第4問の小問2は例年、難易度が高いので、本番で取り組むときは時間切れにならないよう、注意しましょう。
