2001年京大 数学 第4問 は、正八面体に関する問題です。東大の入試では時々現れる正八面体の問題。京大ではどのような内容でしょうか。問題文は以下の通りです。
xyz 空間内の正八面体の頂点 P_1,\cdots,P_6 とベクトル \overrightarrow{v} に対し, k \neq m のとき \overrightarrow{P_k P_m} \cdot \overrightarrow{v} \neq 0 が成り立っているとする。このとき, k と異なる全ての m に対して \overrightarrow{P_k P_m} \cdot \overrightarrow{v} < 0 となるような P_k が存在することを示せ。
図形にベクトルを絡めてくるところが何となく京大っぽい気がします(2008年に平行四辺形の問題が出題されました)。
2001年京大 数学 第4問 の解法
設問の内容は、どういう状況を意味しているのでしょうか。内積が負ということは、2つのベクトルのなす角が鈍角ということです。つまり、 \overrightarrow{v} が正八面体のすべての頂点に対して、そっぽを向いていればよいということになります。
こう考えると、確かに題意を満たす頂点はありそうな気がしてきます。そこで正八面体を、中心に原点 O が来るように平行移動します。平行移動しても \overrightarrow{P_k P_m} \cdot \overrightarrow{v} の値は変わらないので、一般性を失いません(図1)。
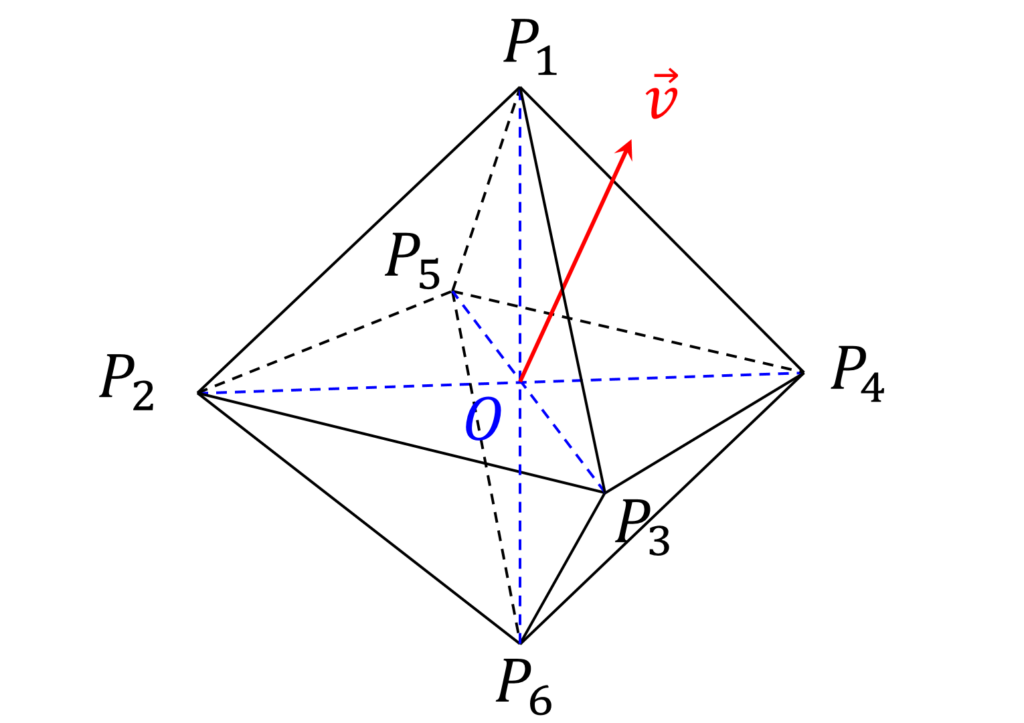
ここで原点と各頂点を結ぶベクトルを
\begin{gathered}
\overrightarrow{p_m} = \overrightarrow{OP_m} \\
(m=1, \cdots,6) \\
\end{gathered}と定義するとき、 k \neq m のとき \overrightarrow{P_k P_m} \cdot \overrightarrow{v} \neq 0 であるので、 \overrightarrow{p_k} \cdot \overrightarrow{v} \neq \overrightarrow{p_m} \cdot \overrightarrow{v} が成り立ちます。
そこで \overrightarrow{p_k} を、 \overrightarrow{v} にもっとも方向が近い(つまり内積 \overrightarrow{p_k} \cdot \overrightarrow{v} が最も大きい)ものであるとします。
k \neq m のとき \overrightarrow{p_k} \cdot \overrightarrow{v} \neq \overrightarrow{p_m} \cdot \overrightarrow{v} なので、そのような \overrightarrow{p_k} を1つだけ選ぶことが出来ます。
すると、確かに \overrightarrow{P_k P_m} = \overrightarrow{p_m} - \overrightarrow{p_k} は \overrightarrow{v} に対してそっぽを向いていますし、内積を計算すると
\begin{aligned}
& \overrightarrow{P_k P_m} \cdot \overrightarrow{v} \\
&= (\overrightarrow{p_m} - \overrightarrow{p_k})\cdot \overrightarrow{v} \\
& = \overrightarrow{p_m} \cdot \overrightarrow{v} - \overrightarrow{p_k} \cdot \overrightarrow{v} < 0
\end{aligned}となります。
ところで、上記の論考は、正八面体を平行移動しなくても成り立ちます。問題を理解しやすくするために平行移動してみましたが、証明には不要なので、回答としては以下のようにまとめるとよいでしょう。
原点 O と各頂点を結ぶベクトルを
\begin{gathered}
\overrightarrow{p_m} = \overrightarrow{OP_m} \\
(m=1, \cdots,6)
\end{gathered}
と定義する。 k \neq m のとき \overrightarrow{P_k P_m} \cdot \overrightarrow{v} \neq 0 であるので、
\overrightarrow{p_k} \cdot \overrightarrow{v} \neq \overrightarrow{p_m} \cdot \overrightarrow{v}
が成り立つ。
したがって、 \overrightarrow{p_m} のなかで \overrightarrow{p_m} \cdot \overrightarrow{v} が最大となるものを \overrightarrow{p_k} と置くと、最大のものはただ一つなので k \neq m のとき
\overrightarrow{p_k} \cdot \overrightarrow{v} > \overrightarrow{p_m} \cdot \overrightarrow{v}
である。ゆえに
\begin{aligned}
& \overrightarrow{P_k P_m} \cdot \overrightarrow{v} \\
&= (\overrightarrow{p_m} - \overrightarrow{p_k})\cdot \overrightarrow{v} \\
& = \overrightarrow{p_m} \cdot \overrightarrow{v} - \overrightarrow{p_k} \cdot \overrightarrow{v} < 0
\end{aligned}
が成り立つ。
本問における正八面体の意味
解法を見ていただくとわかる通り、証明に当たって正八面体と言う条件は使っていません。どんな図形であっても、同じやり方で証明できます。
むしろ、正八面体に固有の性質を使おうと考えすぎると、かえって墓穴を掘る結果になりそうです。
ぱっと見、非常に重要に思える条件が、実は全くどうでもよいという建て付けは、ちょっと意地悪にも感じますが、実はこれは難易度調整の結果であって、当初は鬼のように超ムズな問題だったのかもしれません。
解法のポイント
図形の問題は図を描いてイメージをつかむのが大事ですが、本問のようにベクトルが絡む問題の場合、扱うオブジェクトを平行移動させたり回転させたりして、より分かりやすく配置することがポイントです。
その際に重要なことは、それらの移動によって一般性が失われないことの確認です。本稿の場合は、平行移動によっても正八面体の頂点の相対位置は変わらないため、問題ありませんでしたが、一般性が失われるような移動をかけると、誤った結果が出る可能性があるので、注意しましょう。