ド・モアブル大活躍 – 2016年京大特色入試数学第1問

円周上の点の選択に関する問題です(Pete LinforthによるPixabayからの画像)

2021年10月26日2023年2月28日

2016年京大特色入試数学第1問は数列と極限の問題です。問題文は以下の通りです。

$n$ を2以上の整数とする。原点 O を中心とした半径1の円周を $n$ 等分する点を時計回りに $\mathrm{P}_0,\mathrm{P}_1,\cdots,\mathrm{P}_{n-1}$ とする。これら $n$ 点から無作為に1点を選ぶ試行を独立に3回繰り返し、3点 P, Q, R を順に選ぶ。ただし、P, Q, R は重複を許して選び、どの $n$ 点も同じ確からしさで選ぶものとする。 $0 \leqq j,k,l \leqq n-1$ に対し、P, Q, R がそれぞれ $\mathrm{P}_j,\mathrm{P}_k,\mathrm{P}_l$ である確率を $p_{jkl}$ とする。3点 $\mathrm{P}_j,\mathrm{P}_k,\mathrm{P}_l$ が異なるとき、三角形 $\mathrm{P}_j \mathrm{P}_k \mathrm{P}_l$ の面積を $S_{jkl}$ とおく。また、3点 $\mathrm{P}_j,\mathrm{P}_k,\mathrm{P}_l$ に重複があるとき、 $S_{jkl} = 0$ とおく。

$E_n = \displaystyle\sum_{j=0}^{n-1} \left \{ \displaystyle \sum_{k=0}^{n-1} \left (\displaystyle \sum_{l=0}^{n-1} p_{jkl} S_{jkl} \right ) \right \}$

とおく。 $E_n$ を求めよ。また、 $\lim\limits _{n \rightarrow \infty} E_n$ を求めよ。

　京大の入試問題とは思えない、文面のゴツさです。泥沼計算の予感がします。

1. 2016年京大特色入試数学第1問の解答方針
2. 三角形の面積 $S_{jkl}$ を求める
3. $E_n$ の具体的な表記を求める
4. $E_n$ の $\sum\limits_{k=1}^{l-1} \sum\limits_{j=0}^{k-1}$ 以下を計算する
5. 三角関数の級数を計算する
6. 三角関数級数の計算結果を $E_{l,n}$ に代入する
7. $\sum\limits_{l=2}^{n-1} E_{l,n}$ を計算する
8. $E_n$ とその極限を求める
9. 2016年京大特色入試数学第1問解法のポイント

2016年京大特色入試数学第1問の解答方針

　 $E_n$ を具体的に求める必要がありますが、 $j,l,l$ をでたらめに選ぶと三角形の面積 $S_{jkl}$ の定式化が難しくなるので、順序を固定して $S_{jkl}$ の式を求め、同じ頂点の組み合わせに対して $j,k,l$ の選び方は6通りあるから6倍する、と言うやり方を取ります。

三角形の面積 $S_{jkl}$ を求める

　上記の方針に従って、まず三角形の面積 $S_{jkl}$ を求めます。

$0 \leqq j < k< l \leqq n-1$ とします。このとき

\begin{aligned} \angle \mathrm{P}_j \mathrm{OP}_k & = \theta_1 \\ \angle \mathrm{P}_k \mathrm{OP}_l & = \theta_2 \\ \angle \mathrm{P}_l \mathrm{OP}_j & = \theta_3\\ \end{aligned}

とおくと、

\begin{aligned} \theta_1 & = \frac{2\pi}{n}( k- j) \\ \theta_2 & = \frac{2\pi}{n}( l- k) \\ \theta_3 & = 2\pi +\frac{2\pi}{n} j - \frac{2\pi}{n} l \\ & = 2\pi +\frac{2\pi}{n}( j- l) \\ \end{aligned}

です。

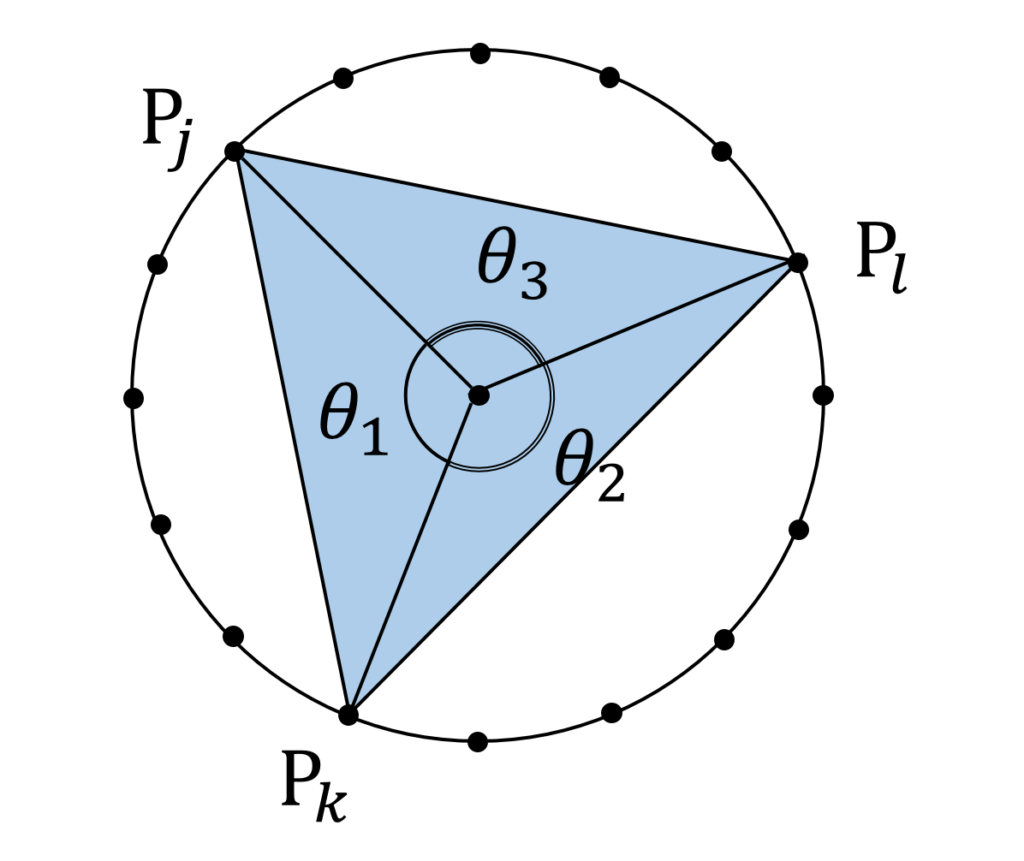
　 $0 < \theta_1,\theta_2, \theta_3 \leqq \pi$ のとき、明らかに

\begin{aligned} S_{jkl} = \frac{1}{2}(& \sin \theta_1 +\sin \theta_2+\sin \theta_3) \\ =\frac{1}{2} \{ & \sin \frac{2\pi}{n}( k- j) \\ + & \sin \frac{2\pi}{n}( l- k) \\ +&\sin (2\pi +\frac{2\pi}{n}( j- l)) \} \\ =\frac{1}{2} \{& \sin \frac{2\pi}{n}( k- j) \\ + & \sin \frac{2\pi}{n}( l- k) \\ + & \sin (\frac{2\pi}{n}( j- l)) \} \\ \end{aligned}

です(図1)。

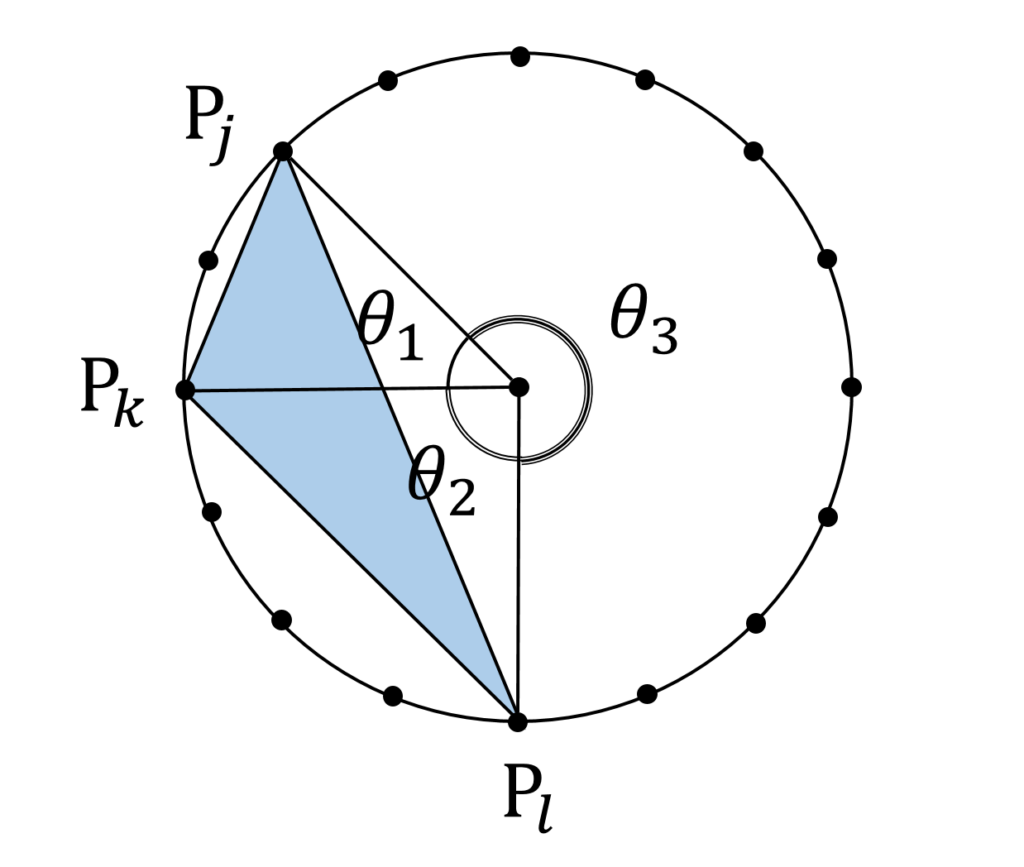
　 $\theta_1,\theta_2, \theta_3$ のどれかが $\pi$ より大きいとき、 $\theta_3 > \pi$ であるとすると、

\begin{aligned} S_{jkl} = \frac{1}{2}(& \sin \theta_1 +\sin \theta_2-\sin (\theta_1 + \theta_2)) \\ =\frac{1}{2} \{ & \sin \frac{2\pi}{n}( k- j) \\ + & \sin \frac{2\pi}{n}( l- k) \\ -&\sin \frac{2\pi}{n}( l -j) \} \\ =\frac{1}{2} \{& \sin \frac{2\pi}{n}( k- j) \\ + & \sin \frac{2\pi}{n}( l- k) \\ + & \sin \frac{2\pi}{n}( j- l) \} \\ \end{aligned}

となります(図2)。 $\theta_1,\theta_2, \theta_3$ の値に関わらず、 $S_{jkl}$ は同一の表記になります。

$E_n$ の具体的な表記を求める

　 $S_{jkl}$ の具体的な式が求められたので、次は $p_{jkl}$ ですが、明らかに $p_{jkl} = \frac{1}{n^3}$ です。

　ところが、頂点P,Q,R と $\{ j,k,l \}$ の組が与えられたとき、P,Q,Rと $\mathrm{P}_j,\mathrm{P}_k,\mathrm{P}_l$ の対応の仕方は3!=６とおりなので、

\begin{aligned} E_n & = \sum_{0 \leqq j,k,l \leqq n-1} \frac{1}{n^3} S_{jkl} \\ & = \sum_{0 \leqq j < k< l \leqq n-1} \frac{6}{n^3} S_{jkl} \\ & = \frac{3}{n^3} \sum_{l=2}^{n-1}\sum_{k=1}^{l-1}\sum_{j=0}^{k-1} \left \{ \sin \frac{2\pi}{n}( k- j) \right . \\ & \text{　　　　　　　　} + \sin \frac{2\pi}{n}( l- k) \\ & \text{　　　　　　　　} + \left . \sin \frac{2\pi}{n}( j- l) \right \} \\ \end{aligned}

となります。

$E_n$ の $\sum\limits_{k=1}^{l-1} \sum\limits_{j=0}^{k-1}$ 以下を計算する

　自然数 $n,l$ に対し

\begin{aligned} E_{l,n} = \sum_{k=1}^{l-1} \sum_{j=0}^{k-1} & \left \{ \sin \frac{2\pi}{n}( k- j) \right . \\ & + \sin \frac{2\pi}{n}( l- k) \\ & + \left . \sin \frac{2\pi}{n}( j- l) \right \} \\ \end{aligned}

と定義します。すると

E_n = \frac 3{n^3} \sum_{l=2}^{n-1} E_{l,n}

です。

第1項の計算

　まず、 $E_{l,n}$ の第1項目は

\begin{aligned} & \sum_{k=1}^{l-1} \sum_{j=0}^{k-1} \sin \frac{2\pi}{n}( k- j) \\ &= \sum_{k=1}^{l-1} \sum_{j=1}^{k} \sin \frac{2\pi}{n} j \\ & = \sin \frac{2\pi}{n}\\ & +\sin \frac{2\pi}{n} +\sin \frac{2\pi}{n} \cdot 2 \\ & +\sin \frac{2\pi}{n} +\sin \frac{2\pi}{n} \cdot 2 +\sin \frac{2\pi}{n} \cdot 3 \\ & + \cdots \\ & +\sin \frac{2\pi}{n} +\sin \frac{2\pi}{n} \cdot 2 +\sin \frac{2\pi}{n} \cdot 3 \\ & \text{　　　　　　　　} + \cdots + \sin \frac{2\pi}{n} l \\ &= (l-1)\sin \frac{2\pi}{n} \\ & +(l-2)\sin \frac{2\pi}{n} \cdot 2 \\ & +(l-3)\sin \frac{2\pi}{n} \cdot 3 \\ & + \cdots \\ & + 2 \sin \frac{2\pi}{n}(l -1)\\ & + 1 \cdot \sin \frac{2\pi}{n}l \\ & = \sum_{k=1}^{l-1} (l-k) \sin \frac{2\pi}{n} k \\ & = \sum_{k=0}^{l-1} (l-k) \sin \frac{2\pi}{n} k \end{aligned}

と計算できます。

第2項の計算

　同様に第2項は　

\begin{aligned} & \sum_{k=1}^{l-1} \sum_{j=0}^{k-1} \sin \frac{2\pi}{n}( l-k) \\ =& \sum_{k=1}^{l-1} k \sin \frac{2\pi}{n}( l-k) \\ =& \sum_{k=1}^{l-1} (l-k ) \sin \frac{2\pi}{n}k \\ =& \sum_{k=0}^{l-1} (l-k ) \sin \frac{2\pi}{n}k \\ \end{aligned}

となります。第1項と同じ計算結果になります。

第3項の計算

　第3項は以下の通りです。

\begin{aligned} & \sum_{k=1}^{l-1}\sum_{j=0}^{k-1} \sin \frac{2\pi}{n}( j-l) \\ &= -\sum_{k=1}^{l-1}\sum_{j=0}^{k-1} \sin \frac{2\pi}{n}( l-j) \\ & = -\sum_{k=1}^{l-1}\sum_{j=l-k+1}^{l} \sin \frac{2\pi}{n}j \\ & = -\sum_{k=2}^{l} (k-1)\sin \frac{2\pi}{n}k \\ & = -\sum_{k=1}^{l} (k-1)\sin \frac{2\pi}{n}k \\ & =-\sum_{k=0}^{l-1} (k-1)\sin \frac{2\pi}{n}k \\ & \text{　} -(l-1)\sin \frac{2\pi}{n}l \\ \end{aligned}

計算結果を足し合わせる

　以上の結果を足し合わせて

\begin{aligned} E_{l,n} = &\sum_{k=0}^{l-1} (l-k) \sin \frac{2\pi}{n} k \\ & + \sum_{k=0}^{l-1} (l-k) \sin \frac{2\pi}{n} k \\ &-\sum_{k=0}^{l-1} (k-1)\sin \frac{2\pi}{n}k \\ & -(l-1)\sin \frac{2\pi}{n}l \\ = & (2l+1) \sum_{k=0}^{l-1} \sin \frac{2\pi}{n}k -3 \sum_{k=0}^{l-1} k \sin \frac{2\pi}{n}k \\ & -(l-1)\sin \frac{2\pi}{n}l \\ \end{aligned}

と計算できました。

三角関数の級数を計算する

ド・モアブルの定理の適用

　上の式で出てきた $\sum\limits_{k=1}^{l-1} \sin \frac{2\pi}{n}k$ や $\sum\limits_{k=1}^{l-1} k \sin \frac{2\pi}{n}k$ を何とかして計算する必要がありますが、ここでド・モアブルの定理の登場です。

　すなわち、 $n$ が整数の時、

(\cos \theta + i \sin \theta)^n = \cos n\theta + i \sin n \theta

が成り立つというのが、ド・モアブルの定理です。 $n$ が負の値でも成り立ちますが、今回使うのは、 $n$ が正の場合です。

　学校で習っていれば、そのまま引用して何の問題もありませんが、万一指導要領から外れていた場合には、複素数の積が偏角の和であることから明らかであると一言断りを入れれば大丈夫です。

$\sum\limits_{k=0}^m \cos kx , \sum\limits_{k=0}^m \sin kx$ の算出

　ここで $z = \cos x + i \sin x$ と置きます。このとき、自然数 $m$ に対し

\begin{aligned} & \sum_{k=0}^m \cos kx + i \sum_{k=0}^m \sin kx \\ & = \sum_{k=0}^m (\cos kx + i \sin kx) \\ & = \sum_{k=0}^m (\cos x + i \sin x)^k \\ & = \sum_{k=0}^m z^k \\ & = \frac{ z^{m+1} - 1}{z- 1} \\ & = \frac{\cos (m+1)x + i \sin (m+1) x - 1}{\cos x +i \sin x- 1} \\ & = \frac{1}{2(1-\cos x)} \\ & \times (\cos x - i \sin x- 1) \\ & \times \{\cos (m+1)x + i \sin (m+1) x - 1 \} \\ & = \frac{1}{ 2- 2\cos x} \\ & \times [ \{ \cos mx - \cos (m+1) x - \cos x + 1\} \\ & \text{　　} + i \{ \sin mx + \sin x -\sin (m+1) x \} ] \end{aligned}

なので、

\begin{aligned} & \sum_{k=0}^m \cos kx \\ & =\frac{\cos mx - \cos (m+1) x - \cos x + 1}{2 -2 \cos x} \\ &= \frac{\cos mx - \cos (m+1) x }{2 -2 \cos x} - \frac{1}{2} \end{aligned}

\begin{aligned} & \sum_{k=0}^m \sin kx \\ & =\frac{\sin mx + \sin x -\sin (m+1) x}{2 -2 \cos x} \\ \end{aligned}

が成り立ちます。

$\sum\limits_{k=0}^m k\sin kx$ の算出

　 $\sum\limits_{k=0}^m \cos kx$ を微分して求めます。

\begin{aligned} & \sum_{k=0}^m k\sin kx \\ & =-\left (\sum_{k=0}^m \cos kx \right)' \\ & =- \left (\frac{\cos mx - \cos (m+1) x }{2 -2 \cos x} - \frac{1}{2} \right)' \\ & = \frac{\sin x \{\cos mx - \cos (m+1) x \}}{2(1- \cos x)^2} \\ & + \frac{m \sin mx - (m+1) \sin (m+1)x}{2(1- \cos x)} \\ \end{aligned}

ですが、

\begin{aligned} & \sin x \cos mx \\ & = \sin x \cos mx + \cos x \sin mx - \cos x \sin mx \\ & = \sin (m+1) x - \cos x \sin mx \\ & \\ & \sin x \cos (m+1) x \\ & = \sin x \cos (m+1 )x - \cos x \sin (m+1) x \\ & \text{　　　　　　　　　} + \cos x \sin (m+1)x \\ & = -\sin mx + \cos x \sin (m+1)x \\ \end{aligned}

なので、

\begin{aligned} & \frac{\sin x \{\cos mx - \cos (m+1) x \}}{2(1- \cos x)^2} \\ & = \frac{ \substack {\sin (m+1) x - \cos x \sin mx \\ +\sin mx - \cos x \sin (m+1)x \\} }{2(1- \cos x)^2} \\ & = \frac{\substack{(1 - \cos x)\sin mx \\+ (1 - \cos x)\sin (m+1)x } }{2(1- \cos x)^2} \\ & = \frac{\sin mx + \sin (m+1)x}{2(1- \cos x)} \\ \end{aligned}

です。したがって、

\begin{aligned} & \sum_{k=0}^m k\sin kx \\ & = \frac{ \sin mx + \sin (m+1)x}{2(1- \cos x)} \\ & + \frac{m \sin mx - (m+1) \sin (m+1)x}{2(1- \cos x)} \\ & = \frac{(m+1) \sin mx - m \sin (m+1)x}{2(1- \cos x)} \\ \end{aligned}

が成り立ちます。

三角関数級数の計算結果を $E_{l,n}$ に代入する

　以下の通りです。

\begin{aligned} E_{l,n} &= (2l+1) \\ & \times \left \{ \frac{\sin \frac{2\pi}{n}(l-1) + \sin \frac{2\pi}{n} -\sin \frac{2\pi}{n}l}{2 -2 \cos \frac{2\pi}{n}} \right \}\\ & -3 \left \{\frac{(l-1) \sin \frac{2\pi}{n}l -l \sin \frac{2\pi}{n}(l-1) }{2(1- \cos \frac{2\pi}{n})} \right \} \\ & -(l-1)\sin \frac{2\pi}{n}l \\ & \\ & = \frac{1-l }{2(1 - \cos \frac{2\pi}{n})}\sin \frac{2\pi}{n}(l-1) \\ & + \left \{ \frac{ 1}{2(1 - \cos \frac{2\pi}{n})} -1 \right \} l \sin \frac{2\pi}{n}l \\ & + \left \{ \frac{ -4}{2(1 - \cos \frac{2\pi}{n})} +1 \right \} \sin \frac{2\pi}{n}l \\ & + \frac{2l+1}{2(1 - \cos \frac{2\pi}{n}) } \sin \frac{2\pi}{n} \\ \end{aligned}

$\sum\limits_{l=2}^{n-1} E_{l,n}$ を計算する

　これまでの結果をもとに、 $\sum\limits_{l=2}^{n-1} E_{l,n}$ を計算します。

\begin{aligned} & \sum_{l=2}^{n-1} E_{l,n} \\ & = \sum_{l=2}^{n-1} \left \{ \frac{1-l }{2(1 - \cos \frac{2\pi}{n})} \sin \frac{2\pi}{n}(l-1) \right \} \\ & + \sum_{l=2}^{n-1} \left [ \left \{ \frac{ 1}{2(1 - \cos \frac{2\pi}{n})} -1 \right \} l \sin \frac{2\pi}{n}l \right ]\\ & + \sum_{l=2}^{n-1} \left [ \left \{ \frac{-4}{2(1 - \cos \frac{2\pi}{n})} +1 \right \} \sin \frac{2\pi}{n}l \right ]\\ &+ \sum_{l=2}^{n-1} \frac{2l+1}{2(1 - \cos \frac{2\pi}{n}) } \sin \frac{2\pi}{n} \\ & = (1) + (2) + (3) +(4) \end{aligned}

を、各項ごとに計算します。

各項ごとの計算

\begin {aligned} & (1) \\ &= - \frac{\sum\limits_{l=0}^{n-2} l \sin \frac{2\pi}{n}l }{2(1 - \cos \frac{2\pi}{n})} \\ &= \frac{ -\sum\limits_{l=0}^{n-1} l \sin \frac{2\pi}{n}l +(n-1) \sin \frac{2\pi}{n}(n-1)}{2(1 - \cos \frac{2\pi}{n})} \\ &= \frac{ -\sum\limits_{l=0}^{n-1} l \sin \frac{2\pi}{n}l + (n-1) \sin (2\pi -\frac{2\pi}{n})}{2(1 - \cos \frac{2\pi}{n})} \\ &= \frac{ -\sum\limits_{l=0}^{n-1} l \sin \frac{2\pi}{n}l + (1-n) \sin\frac{2\pi}{n}}{2(1 - \cos \frac{2\pi}{n})} \\ \end{aligned}

\begin{aligned} (2) & = \left\{ \frac{ 1}{2(1 - \cos \frac{2\pi}{n})} -1 \right \} \sum_{l=0}^{n-1} l \sin \frac{2\pi}{n}l \\ & - \left\{ \frac{ 1}{2(1 - \cos \frac{2\pi}{n})} -1 \right \} \sin \frac{2\pi}{n} \\ & = \frac{ \sum\limits_{l=0}^{n-1} l \sin \frac{2\pi}{n}l}{2(1 - \cos \frac{2\pi}{n})} - \sum_{l=0}^{n-1} l \sin \frac{2\pi}{n}l \\ & -\frac{ \sin \frac{2\pi}{n} }{2(1 - \cos \frac{2\pi}{n})} + \sin \frac{2\pi}{n} \\ \end{aligned}

\begin{aligned} (3) = & \left\{ \frac{ -4}{2(1 - \cos \frac{2\pi}{n})} +1 \right \} \sum_{l=0}^{n-1} \sin \frac{2\pi}{n}l \\ & + \frac{ 4 \sin \frac{2\pi}{n} }{2(1 - \cos \frac{2\pi}{n})} -\sin \frac{2\pi}{n} \\ \end{aligned}

\begin{aligned} (4) &=\frac{\sin \frac{2\pi}{n}}{2(1 - \cos \frac{2\pi}{n}) } \sum_{l=2}^{n-1} (2l+1) \\ & = \frac{(n^2-4)\sin \frac{2\pi}{n}}{2(1 - \cos \frac{2\pi}{n}) } \end{aligned}

です。

各項の計算結果を足し合わせる

　(1)と(2)を足して

\begin{aligned} &(1) + (2) \\ & = - \sum_{l=0}^{n-1} l \sin \frac{2\pi}{n}l - \frac{n \sin \frac{2\pi}{n}}{2(1 - \cos \frac{2\pi}{n})} + \sin \frac{2\pi}{n} \end{aligned}

　これに(3)を足して

\begin{aligned} &(1) + (2) +(3)\\ & = - \sum_{l=0}^{n-1} l \sin \frac{2\pi}{n}l \\ & +\left\{ \frac{ -4}{2(1 - \cos \frac{2\pi}{n})} +1 \right \}\sum_{l=0}^{n-1} \sin \frac{2\pi}{n}l \\ & + \frac{(4-n) \sin \frac{2\pi}{n}}{2(1 - \cos \frac{2\pi}{n})} \end{aligned}

　ここで

\begin{aligned} & \sum_{l=0}^{n-1} \sin \frac{2\pi}{n} l \\ & =\frac{\sin \frac{2\pi}{n}(n-1) + \sin \frac{2\pi}{n} -\sin \frac{2\pi}{n}n }{2(1 - \cos \frac{2\pi}{n})} \\ & = \frac{\sin (2\pi -\frac{2\pi}{n}) + \sin \frac{2\pi}{n} }{2(1 - \cos \frac{2\pi}{n})} \\ & = 0 \\ &\\ & \sum_{l=0}^{n-1} l \sin \frac{2\pi}{n} l \\ & = \frac{n\sin \frac{2\pi}{n}(n-1) - (n-1) \sin \frac{2\pi}{n} n}{2(1 - \cos \frac{2\pi}{n})} \\ & =\frac{-n\sin \frac{2\pi}{n} } {2(1 - \cos \frac{2\pi}{n})} \\ \end{aligned}

を代入して

\begin{aligned} &(1) + (2) +(3)\\ & = \frac{n\sin \frac{2\pi}{n} } {2(1 - \cos \frac{2\pi}{n})} + \frac{(4-n) \sin \frac{2\pi}{n}}{2(1 - \cos \frac{2\pi}{n})} \\ &= \frac{4 \sin \frac{2\pi}{n}}{2(1 - \cos \frac{2\pi}{n})} \end{aligned}

最終的な計算結果

　上記の結果より、

\begin{aligned} & \sum_{l=2}^{n-1} E_{l,n} = (1) +(2)+(3) +(4) \\ & = \frac{4 \sin \frac{2\pi}{n}}{2(1 - \cos \frac{2\pi}{n})} + \frac{(n^2-4)\sin \frac{2\pi}{n}}{2(1 - \cos \frac{2\pi}{n}) } \\ & = \frac{n^2 \sin \frac{2\pi}{n}}{2(1 - \cos \frac{2\pi}{n})} \\ & = \frac{n^2 \cos \frac{\pi}{n}}{2 \sin \frac{\pi}{n}} \end{aligned}

を得ます。

$E_n$ とその極限を求める

　以下の通りです。

\begin{aligned} E_n &= \frac{3}{n^3} \sum_{l =2}^{n-1} E_{l,n} \\ & = \frac{3}{n^3}\frac{n^2 \cos \frac{\pi}{n}}{2 \sin \frac{\pi}{n}}\\ & = \frac{3 \cos \frac{\pi}{n}}{2n \sin \frac{\pi}{n}} \end{aligned}

\begin{aligned} \lim_{n \rightarrow \infty} E_n & = \lim_{n \rightarrow \infty} \frac{3 \cos \frac{\pi}{n}}{2n \sin \frac{\pi}{n}} \\ & = \lim_{n \rightarrow \infty} \frac{3 \cos \frac{\pi}{n}}{2 \pi \frac{\sin \frac{\pi}{n}}{ \frac{\pi}{n}}} \\ & = \frac{3}{2\pi} \end{aligned}

2016年京大特色入試数学第1問解法のポイント

とにかく計算を頑張りましょう（StockSnapによるPixabayからの画像）

　本問はとにかく計算が大変です。ミスしないよう、計算力をつけておきましょう。

　途中に出てくる三角関数級数 $\sum\limits_{k=0}^m \sin kx, \sum\limits_{k=0}^m l\sin kx$ の計算には、ド・モアブルの定理が便利です。この手の級数が出てきたときは、これが使えないか検討しましょう。

　また、途中に出てきた

\begin{aligned} & \sum_{k=1}^{l-1} \sum_{j=1}^{k} \sin \frac{2\pi}{n} j \\ & = \sin \frac{2\pi}{n}\\ & +\sin \frac{2\pi}{n} +\sin \frac{2\pi}{n} \cdot 2 \\ & +\sin \frac{2\pi}{n} +\sin \frac{2\pi}{n} \cdot 2 +\sin \frac{2\pi}{n} \cdot 3 \\ & + \cdots \\ & +\sin \frac{2\pi}{n} +\sin \frac{2\pi}{n} \cdot 2 +\sin \frac{2\pi}{n} \cdot 3 \\ & \text{　　　　　　　　} + \cdots + \sin \frac{2\pi}{n} l \\ & = \sum_{k=1}^{l-1} (l-k) \sin \frac{2\pi}{n} k \end{aligned}

と展開するロジックも重宝します。同じ要素を複数回足しこむような級数和が出てきたときは、適用を検討してみてください。

ブログトップページに戻る

京大受験は(有)峰企画の家庭教師

京大2016年

Posted by mine_kikaku

2016年京大 特色入試 数学 第1問 の解答方針

三角形の面積 S_{jkl} を求める

E_n の具体的な表記を求める

E_n の \sum\limits_{k=1}^{l-1} \sum\limits_{j=0}^{k-1} 以下を計算する