中学入試を考える

2022年5月7日2023年2月27日

先日、朝日新聞に、中学入試に関する以下のような記事が載っていました。

算数、合否を分けた問題は　開成、渋渋、豊島岡　中学入試分析・後編

昔に比べて難しくなった、みたいな内容でしたが、その中で、渋谷学園渋谷中学の入試問題が引用されていました（以下のリンク先の画像）。

渋谷教育学園渋谷の2月1日入試で出された算数の問題

　どれどれ、と見てみました。問題は図形の面積に関するもので、3つの小問から構成されていますが、信じられないくらい難しい問題です。

2022年渋渋算数 第3問(1) の内容

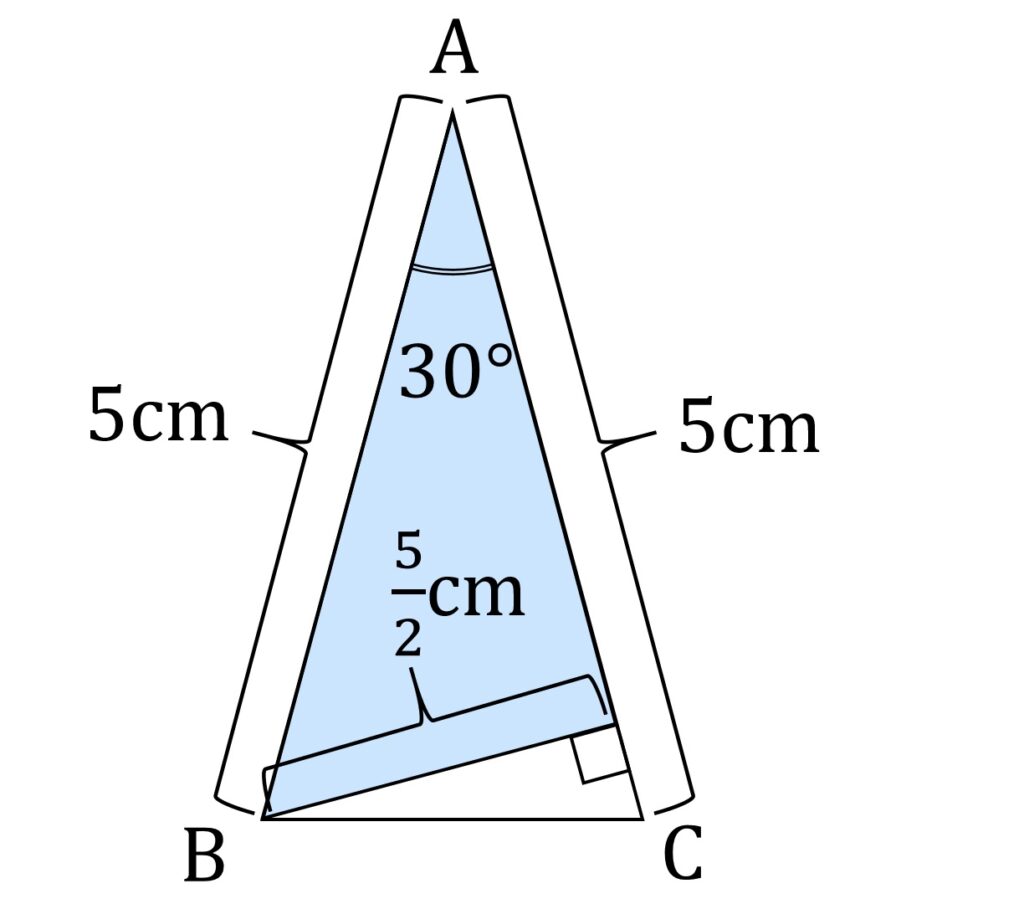
　小問1は、以下の図1の三角形の面積を求めよ、と言う問題です。

　小学校で三角形の面積は底辺×高さ÷２だろうが。こんなのどうやって計算するんだよ、と思いましたが、答えに無理数とか出てこないことを確認するために、三角形の2辺 a,b とはさむ角θが与えられたときの面積の公式

S = \frac{1}{2}ab \sin \theta

で計算しようとしたところで、 \sin 60 ^ \circ = \frac {1}{2} なのだから、B から AC に垂らした垂線の長さは \frac{5}{2} だと気が付きました(図1-1)。確かに底辺×高さ÷2の公式に帰着できて、小学生にも解けそうです。30°とか60°とかが出てきたときに、三角定規型三角形の辺の比が2:1になることを利用する、という知恵を持っている必要はありますが、このくらいなら中学入試として有りかな、とも思います。