2022年渋渋算数 第3問(2) の内容
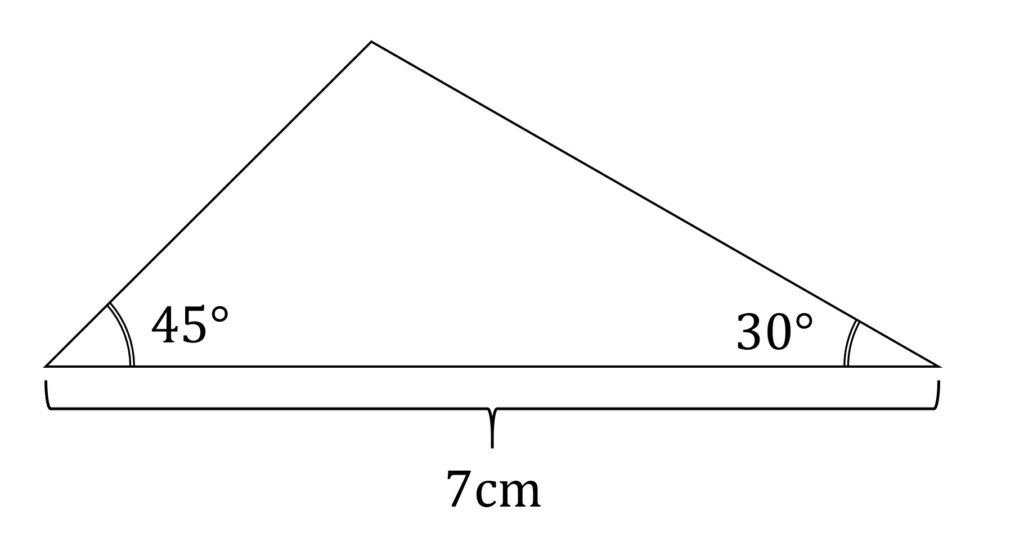
小問2が超絶難問です。図2の三角形と、1辺の長さがその長辺に等しい正三角形の面積の差を求めよ、と言う問題です。
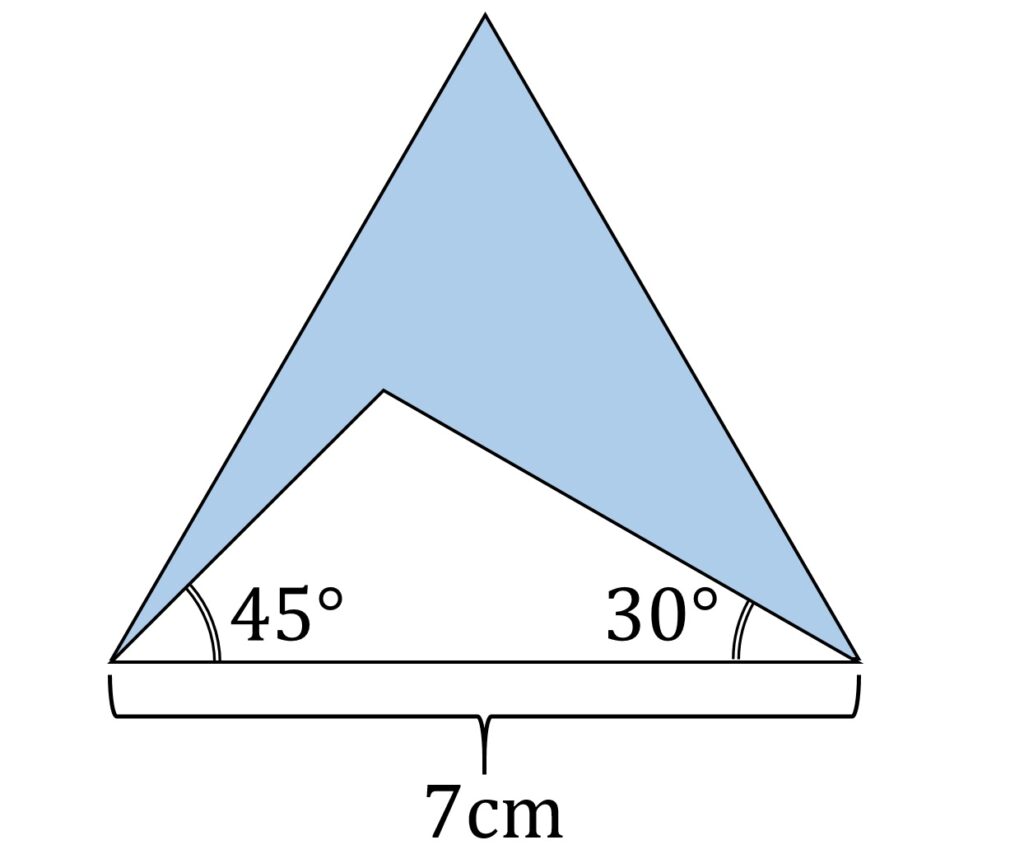
求める面積は、以下の図2-1の網掛け部分です。
以下の図3を使って考えてみてください、と言うことですが、これがヒントとしては全然足りません。
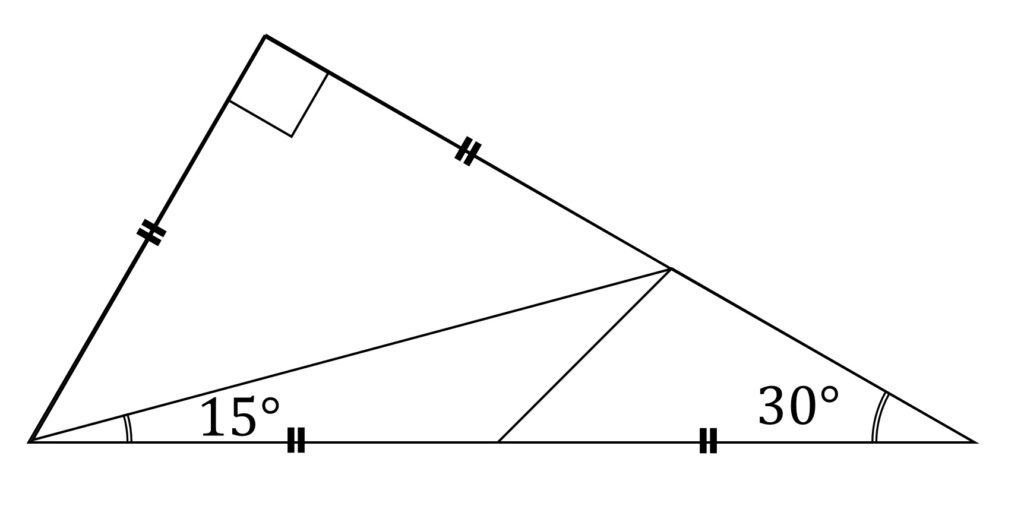
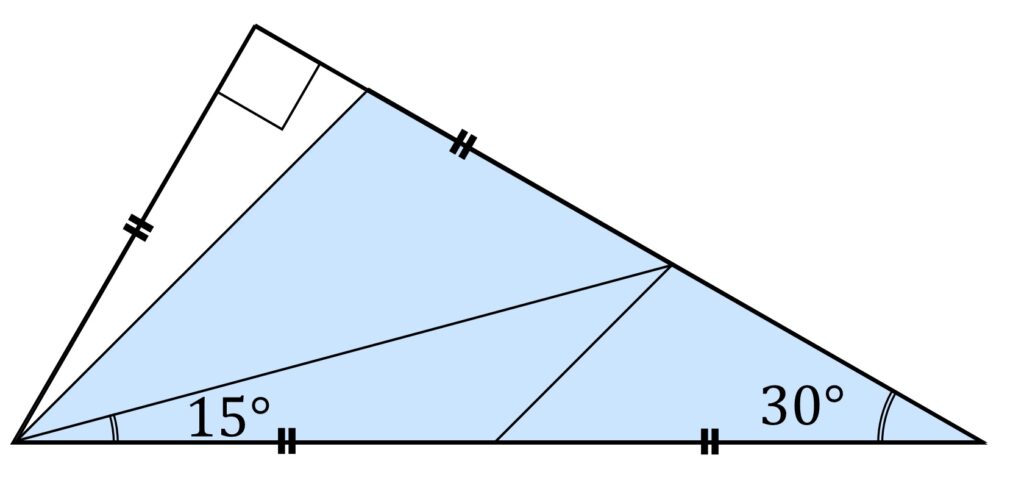
図3-1のように、図2と図3を重ねてみるのかな、というのは外れです。
以下の段取りで攻略します。
補助線を引く
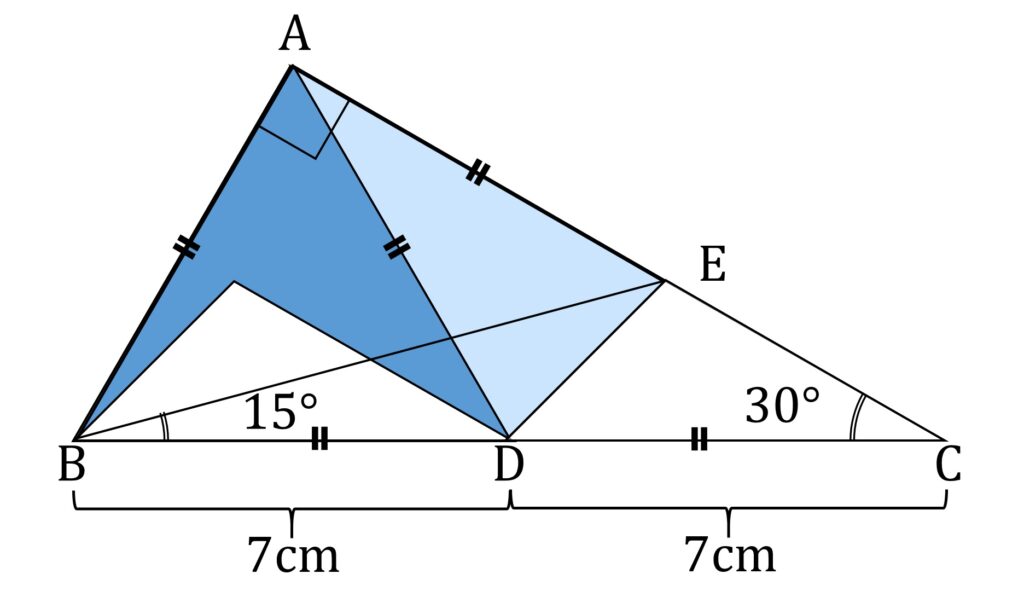
図3の各頂点に図3-2のように記号を振り、A と D を直線で結びます。すると、∠ABC = 60° であることから △ABD は正三角形です。
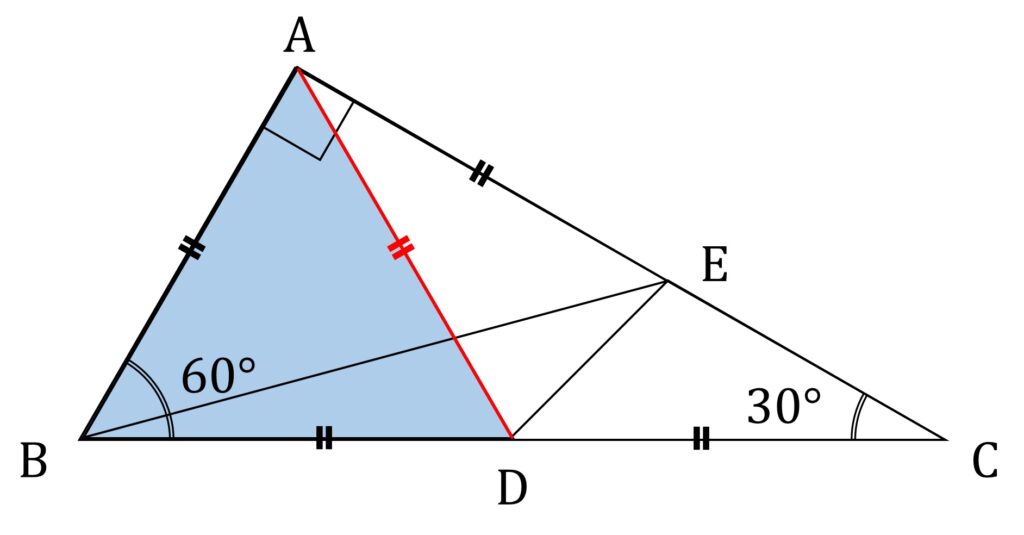
したがって AB = AD ですが、 AB = AE なので AD = AE 、すなわち △ADE は二等辺三角形です。しかも、
∠DAE = ∠BAC – ∠BAD = 90° – 60° = 30°
なので、 △ADE は小問1の三角形と相似であり、 AD の長さが決まれば面積を求めることが出来ます(図3-3)。
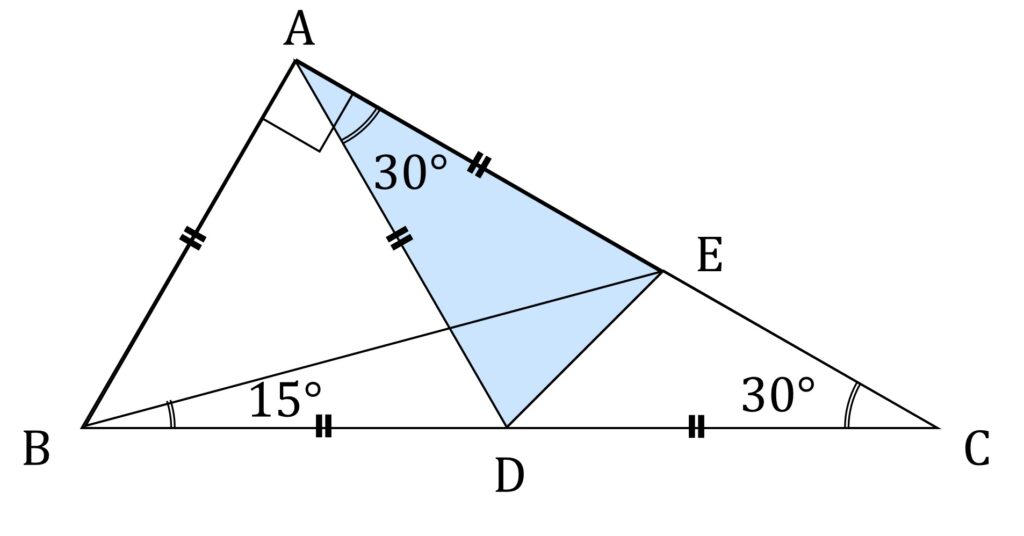
図2の三角形と相似な三角形を探す
図3-2において、図2の三角形と相似な三角形を探します。すると、 ∠ADC = 120° 、∠ADE = 75° であることから、 ∠EDC = 45° であることがわかります。したがって △EDC は図2の三角形と相似です。DC = 7cm とおけば、同じ三角形です(図3-4)。
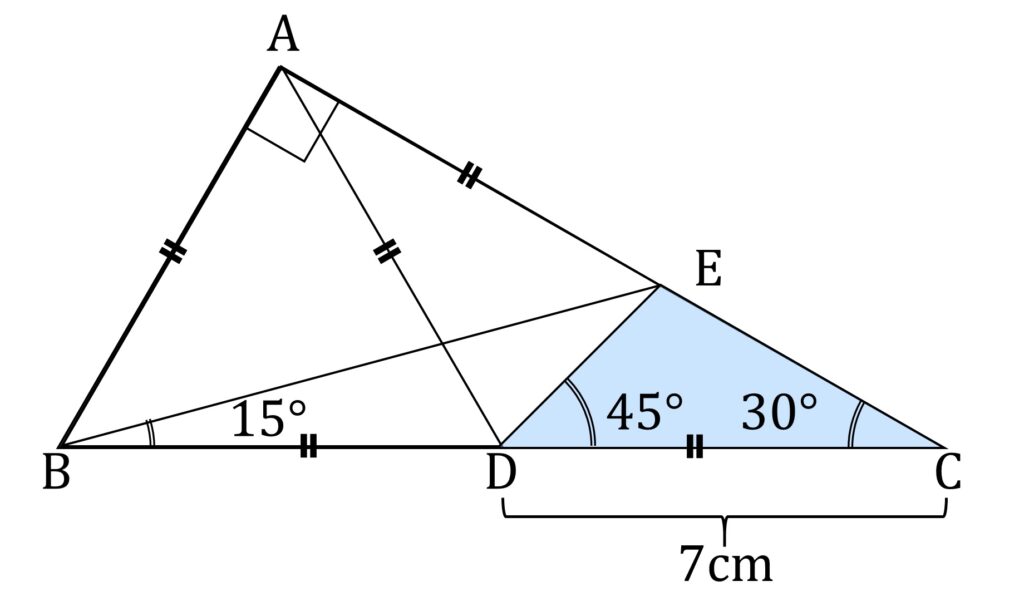
△ABD と △ADC の面積が等しいことに気づく
これは簡単です。 BD = DC なのですから、当然2つの三角形の面積は等しくなります(図3-5)。
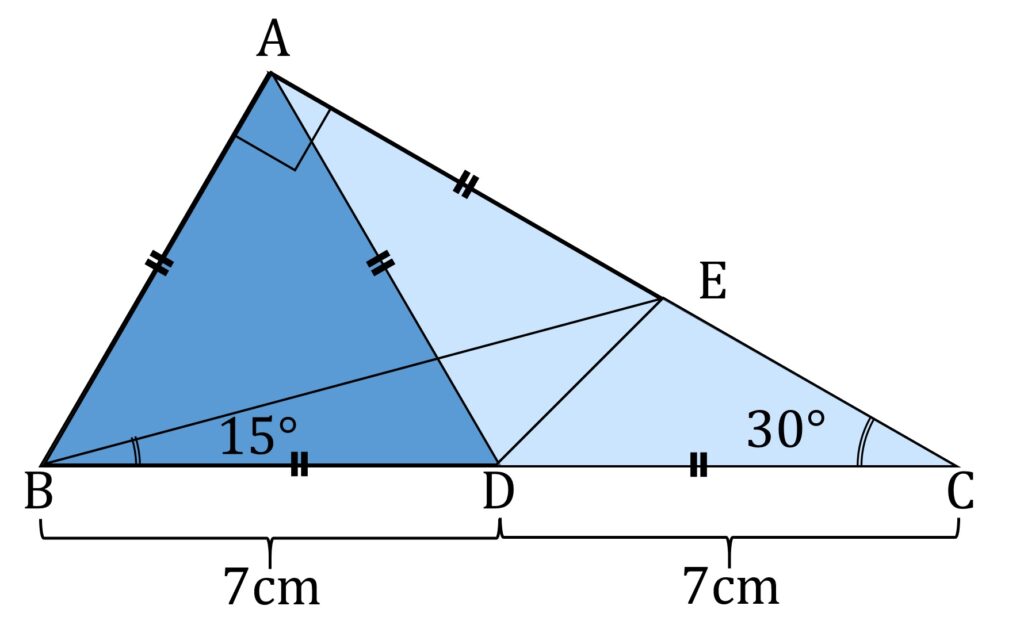
ここで重要なのは、 △ABD が正三角形で、しかも1辺の長さが DC と等しいことです。すなわち、 △EDC の底辺 DC と1辺の長さが等しい正三角形 ABD の面積は、△EDC と △ADE の和なので、求める面積は △ADE の面積となります(図3-6)。
ゆえに求める面積は
7 \times \frac{7}{2} \div 2 = \frac{49}4です。
解き方のまとめ
整理すると、以下の通りです。
- 図3に補助線を引く
- △ADE が小問1の三角形と相似であることに気づく
- 図2の三角形が △EDC と相似であることに気づく
- 1辺の長さが DC と等しい正三角形の面積は、 △ADC の面積に等しいことに気づく
- △ADC の面積は △EDC と △ADE の和である。よって AB=AD=DC=7cm とするとき、求める面積は △ADE の面積で、これは小問1の方法で求めることが出来る
これに加えて、三角形の相似の概念を持っている必要があります。いくら難関校とはいえ、いささか度を越しているのでは、と思える難易度です。