2022年渋渋算数 第3問(3) の内容
小問3は以下の図4における、色のついた部分の面積を求めよ、というものです。
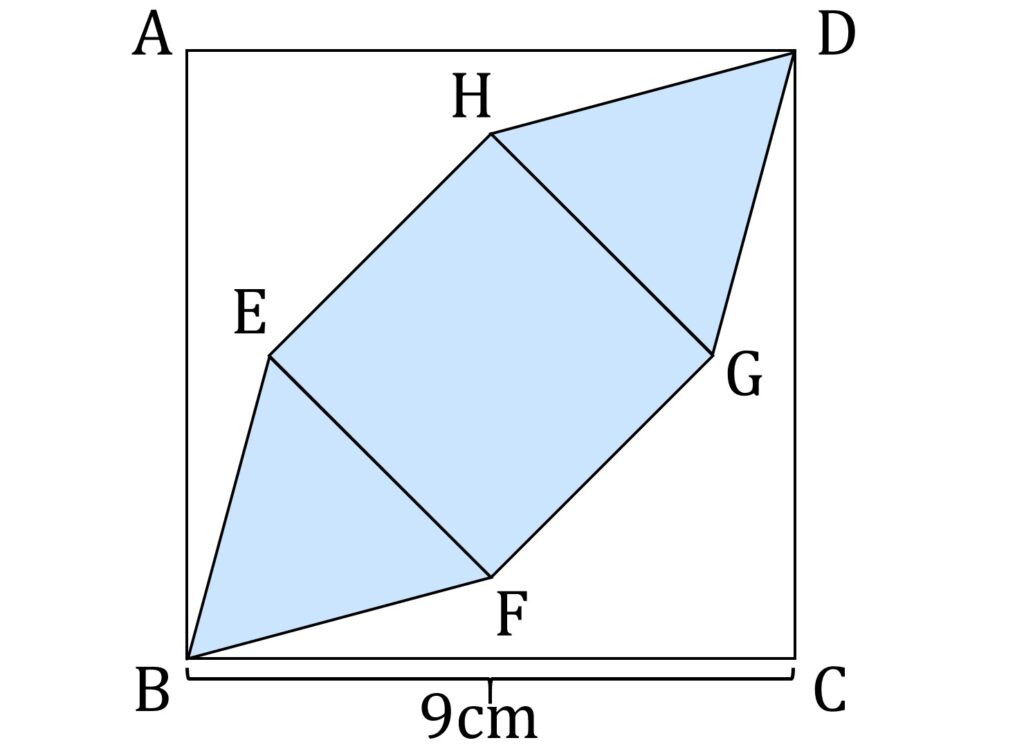
ここに各四角形と三角形はそれぞれ、正方形と正三角形です。
この問題で一番意地悪なのは、解き方が小問2の結果に無関係なところです。あんなに苦労させておいて何だよ。
どうやって解くかと言うと、まず∠ABFが75°であることに気づくことです。このことから、AとF、AとGをそれぞれ結んだときに、△ABF、△AFG、△AGDがそれぞれ小問1の三角形と同じ形であるという発想の大跳躍に到達する必要があります(図4-1)。
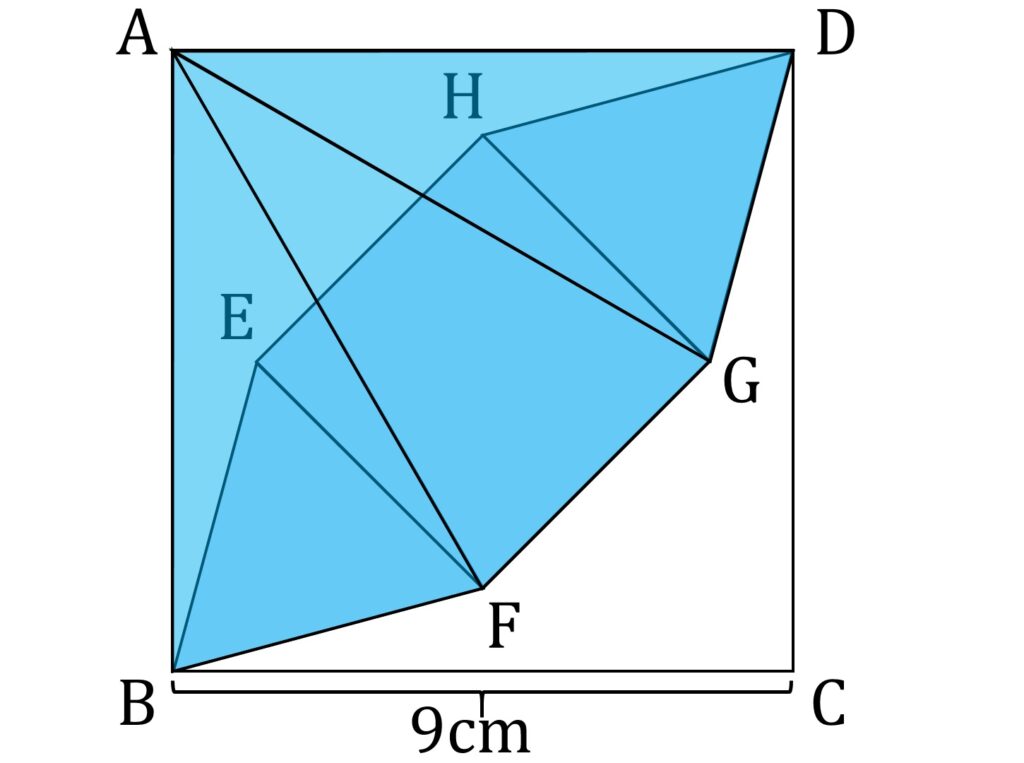
これが思いつければ、各三角形の面積は小問1の方法で求められるので、図4-1の白抜き部分の面積が計算でき、答えにたどり着くことが出来ます。
ところが、△ABFが二等辺三角形であることを証明するのが、一筋縄ではいきません。どうやるかですが、まず、AとE、AとH、CとF,CとGをそれぞれ結びます。すると △AEH および △CFG は正三角形で、しかも各辺の長さは △EBF や △HGD と等しくなります(図4-2)。
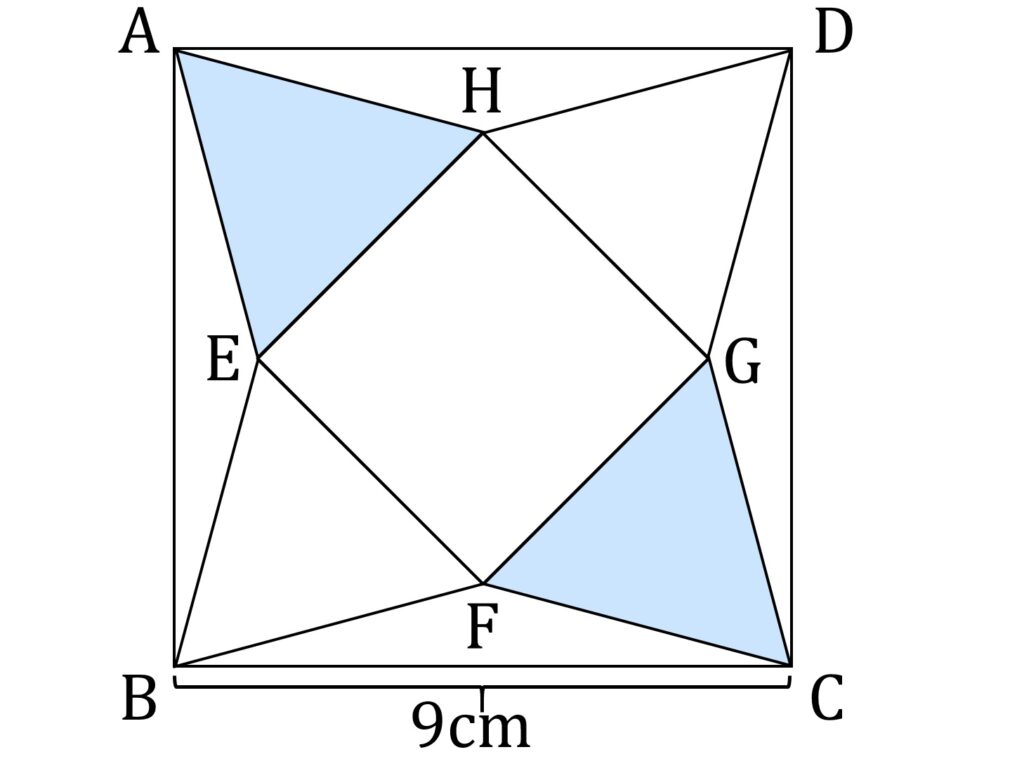
図4-2の図形全体は、正方形ABCDの中心を回転軸として、90度回転させても、元の図形と完全に一致します(小学生の履修範囲でこれを証明するのは著しく困難ですが、感覚的には明らかだと思います)。したがって、△EABと△FBCは合同であり、またそれぞれの三角形は二等辺三角形なので、∠EBC=∠FBCが成り立ちます(図4-3)。
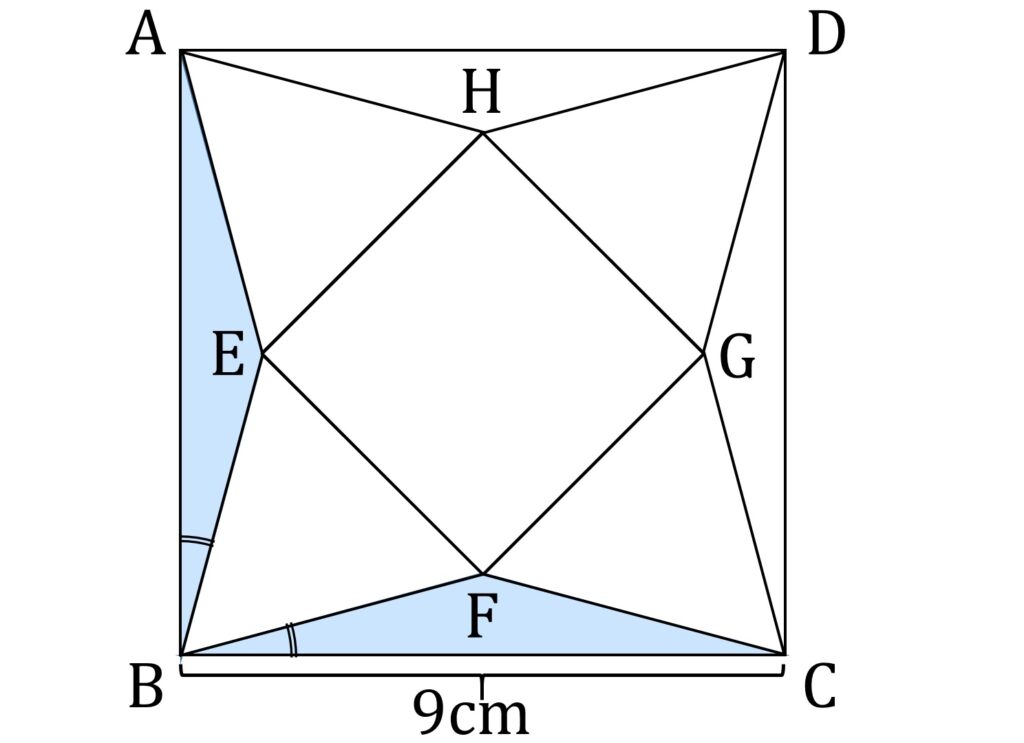
よって、∠ABC=90°、∠EBF=60°であることから、
∠EBA = ( 90°- 60°) ÷ 2 = 15°
であり、したがって
∠ABF = ∠ABF + ∠EBF = 15°+ 60°= 75°
です。
次に、∠AFB=75°を示しますが、これがまた大変です。△EAFにおいて EA=EF なので、この三角形は二等辺三角形です。一方、
∠AEF = ∠AEH + ∠HEF = 60°+ 90°= 150°
なので ∠EFA = 15°です(図4-4)。
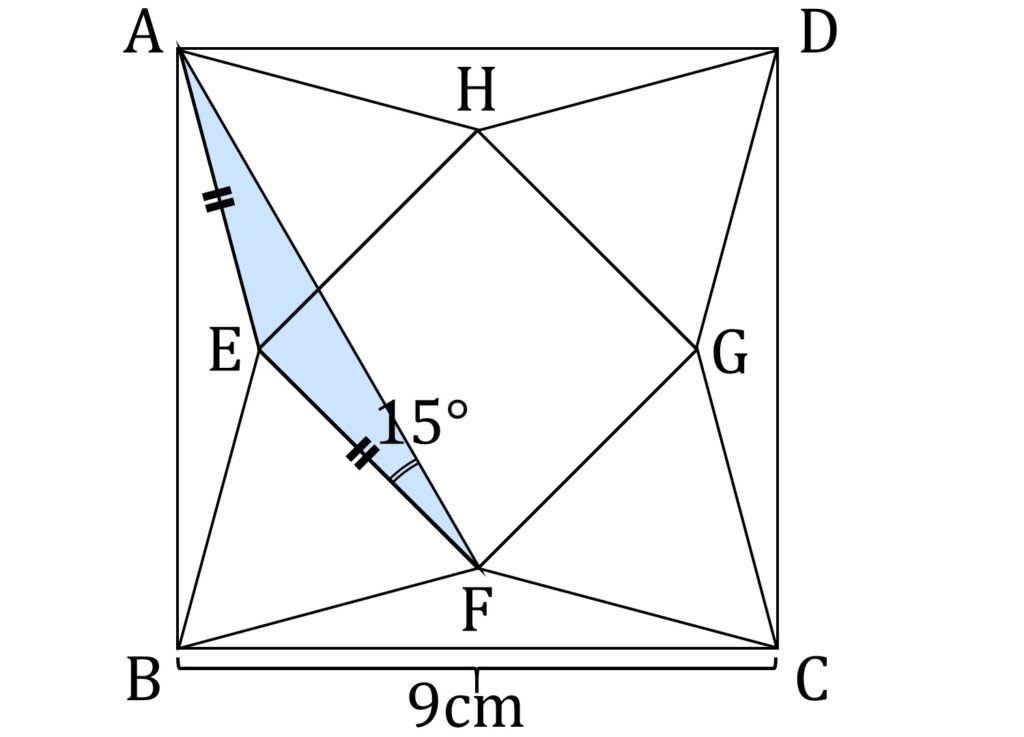
∠AFB = ∠AFE + ∠EFB であることから、ようやく ∠AFB=75°であることが示せました。
底角が等しいので、△ABF は二等辺三角形でかつ、小問1の三角形と相似です。同様にして、 △AGD も二等辺三角形でかつ、小問1の三角形と相似です。
△ABF は二等辺三角形なので AB = AF 、また △AGD は二等辺三角形なので AG = AD です。四角形 ABCD は正方形なので AB = AD ですから、 AF = AG が成り立ち、△AFG は二等辺三角形でかつ、 ∠FAG = 30°なので、小問1の三角形と相似です(図4-5)。
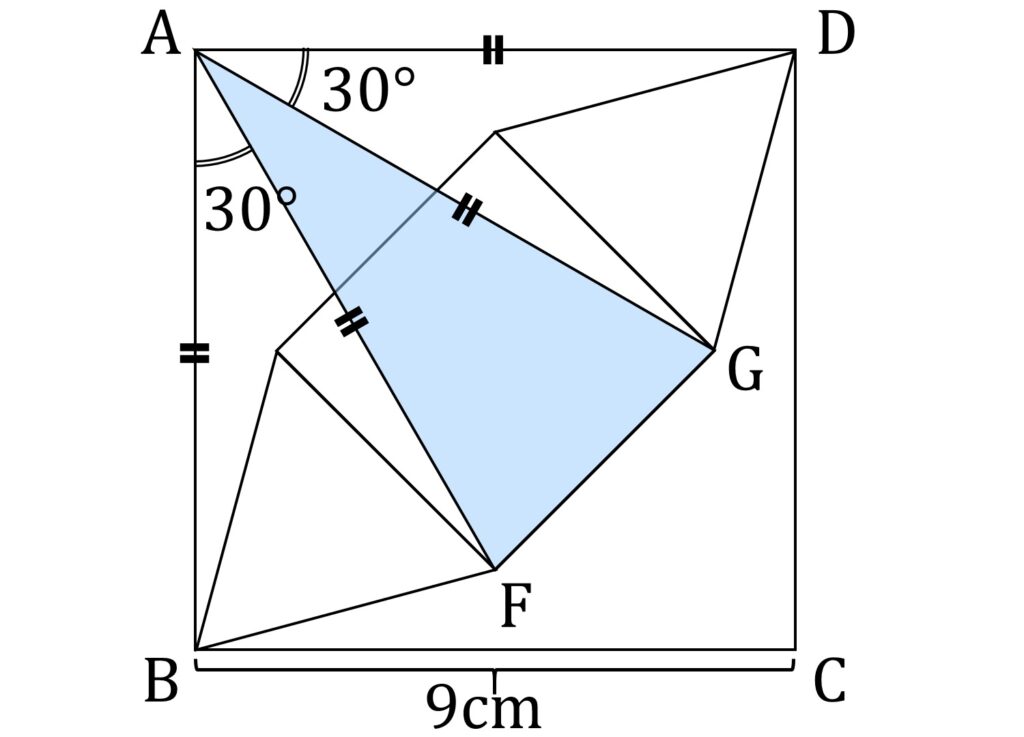
以上の長い長い準備を経て、ついに図4-1の着色部分の面積を求めることが出来ます。その値は
9 \times \frac{9}2 \div 2 \times 3 = \frac{243}4です。よって図4-1の白抜き部分の面積は
9 \times 9 - \frac{243}4 = \frac{81}4です。
ゆえに求める面積は
9 \times 9 - \frac{81}4 \times 2 = \frac{81}2です。元の正方形の、ちょうど半分でした。
いかがでしょうか。小学生がこの問題を解くのと、高校生が例えば京大の「自分で得点を決められる問題」を解くのとどちらが楽かと言ったら、筆者は圧倒的に京大のほうが楽だと思ってしまいます。そこで、本問がなぜそんなに難しく感じるのか、その理由を考えてみました。