中学入試を考える

2022年5月7日2023年2月27日

難しさの源泉は知識の制約から

　本問を解くにあたって、例えば三平方の定理と方程式を解禁したらどうなるでしょうか。中学レベルの知識を前提としたときには、教科書レベルよりちょっと難しいくらいの陳腐な問題に、たちどころに成り下がってしまいます。

　小問2で三角形の高さを h と置くと、

h + \sqrt{3} h = 7

なので、

h = \frac{7}{1 + \sqrt{3}}

です（図5）。

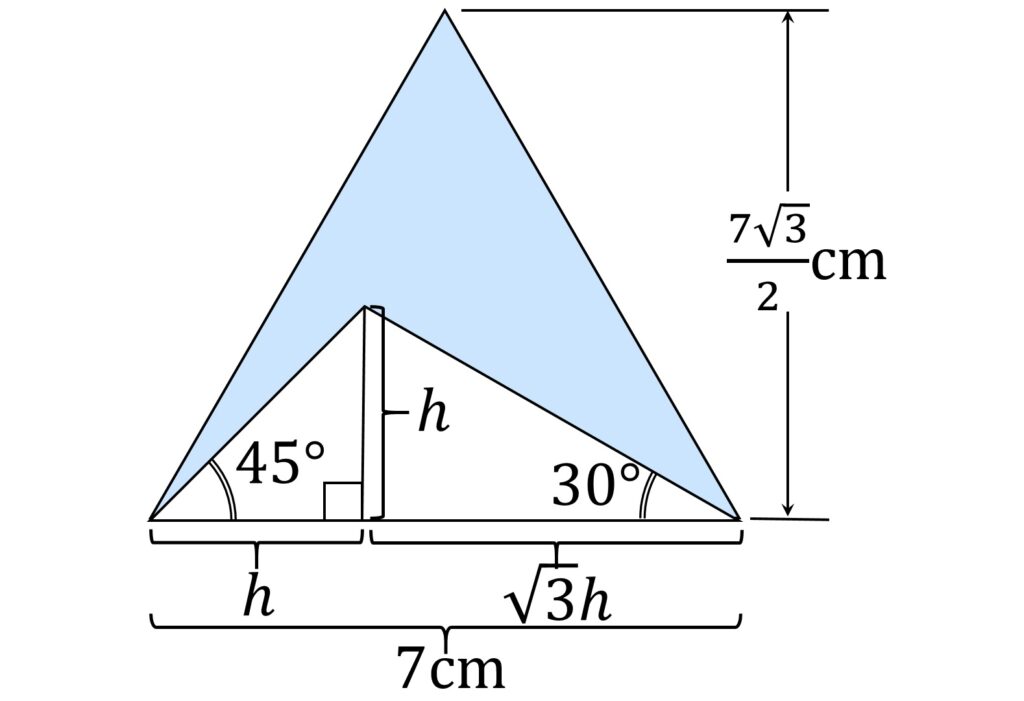
　よって求める面積は

\begin{aligned} & \frac{49 \sqrt{3}}{4} -\frac{49}{2(1+\sqrt{3})} \\ = &\frac{49 \sqrt{3}}{4} - -\frac{49(\sqrt{3} - 1)}{4} \\ =& \frac{49}{4} \end{aligned}

です。

　小問3の方は、内側の正方形／正三角形の一辺の長さを $a$ と置くと、

2 \cdot \frac{ \sqrt{3}}{2} a +a = 9 \sqrt {2}

なので

a = \frac{9 \sqrt {2} }{1 + \sqrt{3}} = \frac{9 \sqrt 2 (\sqrt 3 - 1)}{2}

です（図6）。

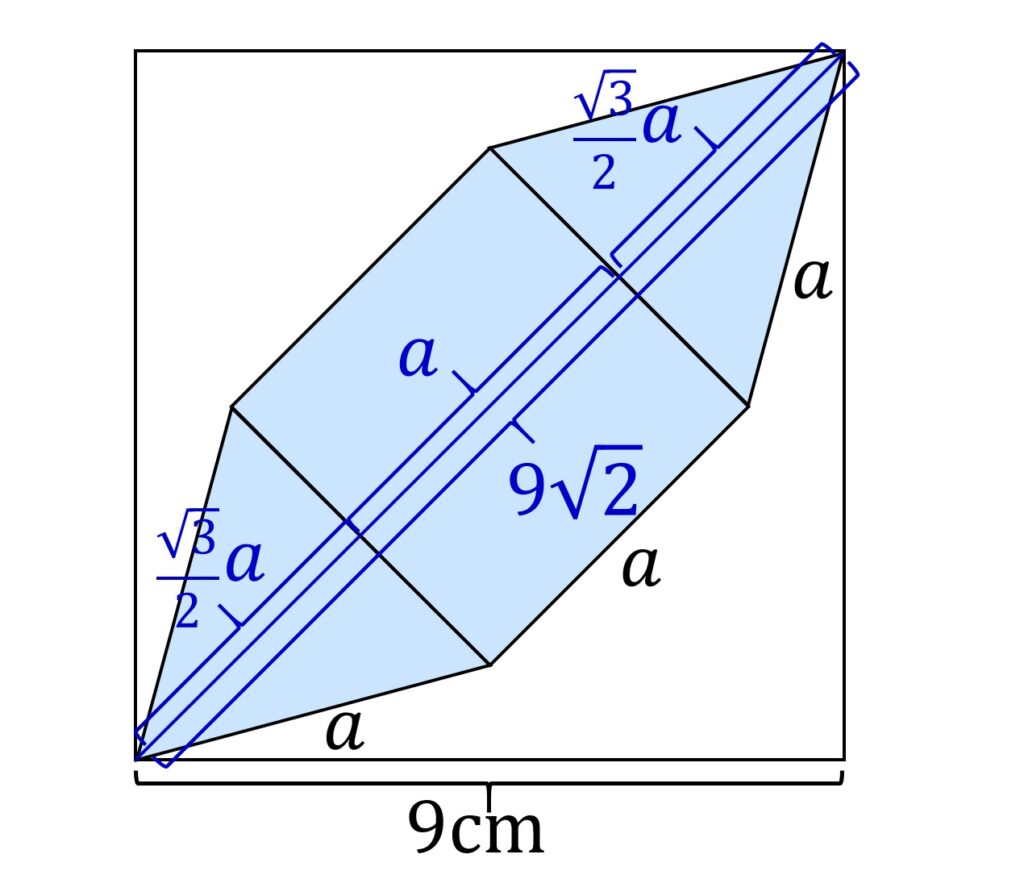
　よって求める面積は

\begin{aligned} & 2 \cdot \frac{\sqrt 3 a^2}{4} + a^2 \\ = & \frac{2 + \sqrt 3} 2 a^2 \\ = &\frac{2 + \sqrt 3} 2 \cdot \frac{162( \sqrt 3 - 1)^2}{4} \\ = & \frac{2 + \sqrt 3} 2 \cdot \frac{81 (4 - 2\sqrt 3)} 2 \\ = & \frac{2 + \sqrt 3} 2 \cdot 81 (2 - \sqrt 3) \\ = & \frac{81}2 \end{aligned}

です。

　つまり難しさの源泉は、小学校レベルの知識で中学3年の問題を解かせようとするところにあります。学校側から見れば、なるべく多くの優秀な生徒を集めたいのですから、入試問題の難易度がエスカレートしていくのはやむを得ないことかも知れませんが、筆者などは、どうせ先に行けばわかるようになるのだから、受験生の立場ではそんなに慌てなくても良いのではないか、と思ってしまいます。

中学入学時点で難問が解けなくても全然オッケー

　本問が解けるほどの学力の人にとっては、中学受験の意味はもちろんあって、体系数学などの独自のカリキュラムは魅力的です。

　しかし、中学受験し、それに合格することが難関大学受験のための必要条件かと言うと、この難易度を見るにつけ、必ずしもそうではないのではないか、と考えます。

　先にも書いたように、入試問題がどう見ても必要以上に難しい上に、わずか数年で陳腐化してしまうからですが、そもそも、難関中学に入ったから難関大学に入学できるようになるのか、それとももともと優秀な生徒を集めているから、合格率が高くなっているのでしょうか。筆者は案外、後者のファクターが大きいのではないかと考えています。

　そんなわけで、中高一貫校に入学しなくても、東大、京大等の難関大入試は全然大丈夫です。中学、高校の6年間でキャッチアップは十分可能であって、成績向上のポイントは