2022年 京大 特色入試 第2問 の定式化
中心角に着目する
とは言うものの、頂点が5つもあって、それらを自由に動かすのですから、いずれかの頂点を固定したとしても変数は4つということになり、一筋縄では行きません。
とりあえず、五芒星の角の三角形の面積 S_i,i=1,2, \cdots ,5 を定式化しようと考えましたが、各辺の長さが頂点の位置によって変わるので、ちょっと手に負えません。
何か、固定的な値を使って面積を出せないかと考えているうちに、各頂点と円の中心 O を結んでできる三角形は二等辺三角形で、かつ等辺の長さが1なのだから、中心角だけで面積が表されるのではないか、と気づきました。
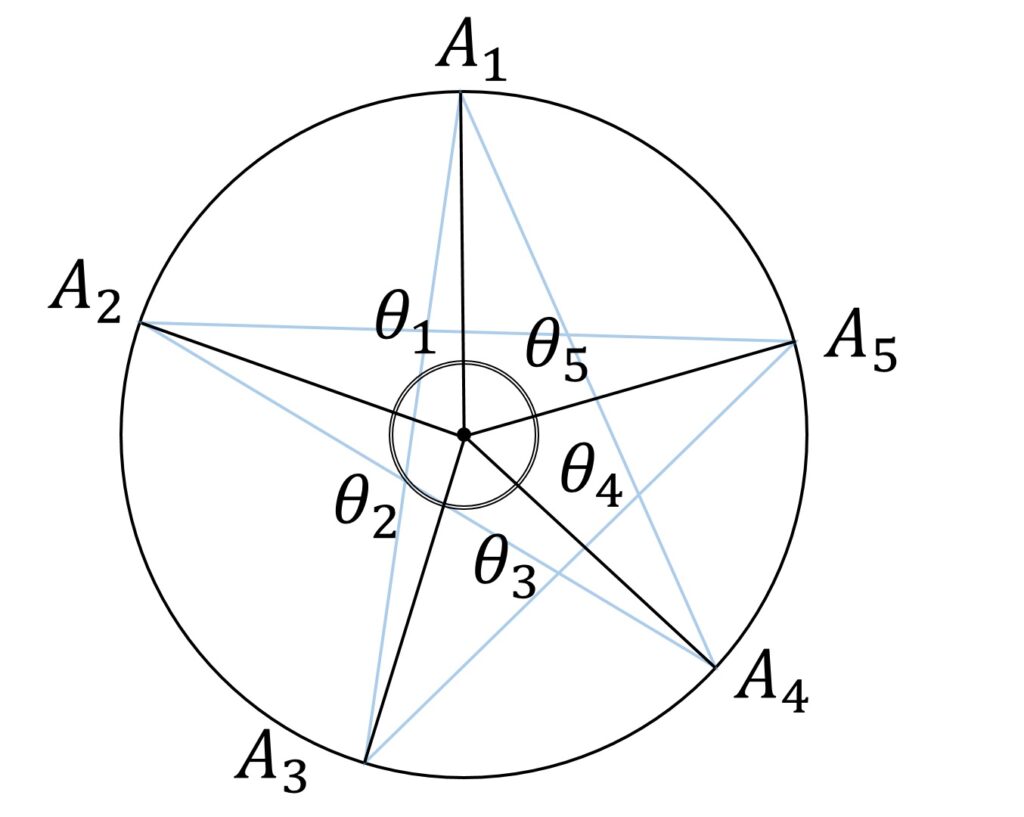
すなわち、
\begin{aligned}
\theta_1 & = \angle A_1 O A_2 \\
\theta_2 & = \angle A_2 O A_3 \\
\theta_3 & = \angle A_3 O A_4 \\
\theta_4 & = \angle A_4 O A_5 \\
\theta_5 & = \angle A_5 O A_1 \\
\end{aligned}と置きます。このとき、
\theta_1 + \theta_2 + \theta_3 + \theta_4 + \theta_5 = 2 \pi
です(図2)。
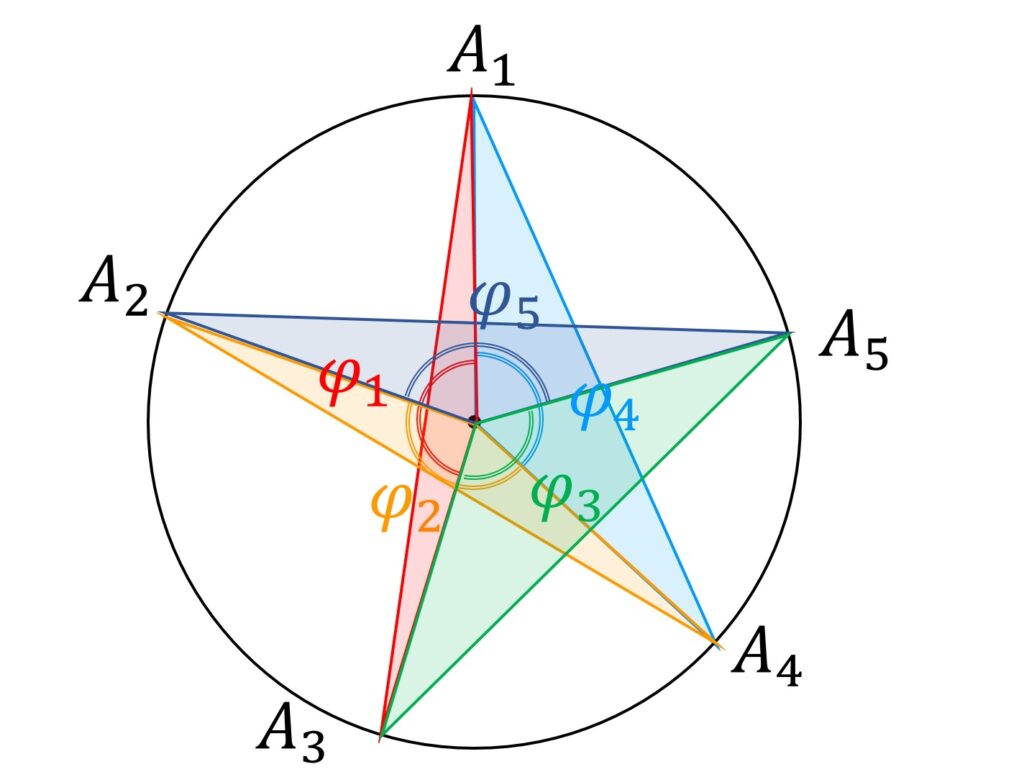
ここで、
\begin{aligned}
\phi_1 & = \theta_1 + \theta_2 \\
\phi_2 & = \theta_2 + \theta_3 \\
\phi_3 & = \theta_3 + \theta_4 \\
\phi_4 & = \theta_4 + \theta_5 \\
\phi_5 & = \theta_5 + \theta_1 \\
\end{aligned}と置きます。すると明らかに
\begin{aligned}
\sum_{i=1}^5 \phi_i = 2 \sum_{i=1}^5 \theta_i = 4\pi
\end{aligned}かつ、
0 < \phi_1,\phi_2,,\phi_3,\phi_4,\phi_5 < 2 \pi
です。
すべての \phi_i,i=1,2,\cdots ,5 がπ以下の場合
まず、
\begin{aligned}
0 & < \phi_1 \leqq \pi \\
0 & < \phi_2 \leqq \pi \\
0 & < \phi_3 \leqq \pi \\
0 & < \phi_4 \leqq \pi \\
0 & < \phi_5 \leqq \pi \\
\end{aligned}の場合を考えます。
このとき、二等辺三角形 \triangle A_1OA_3, \triangle A_2OA_4 , \triangle A_3OA_5 , \triangle A_4OA_1,\triangle A_5OA_2 の面積は、三角形の表記がその面積を表すものとすると、
\begin{aligned}
\triangle A_1OA_3 = \frac{1}2 \sin \phi_1 \\
\triangle A_2OA_4 = \frac{1}2 \sin \phi_2 \\
\triangle A_3OA_5 = \frac{1}2 \sin \phi_3 \\
\triangle A_4OA_1 = \frac{1}2 \sin \phi_4 \\
\triangle A_5OA_2 = \frac{1}2 \sin \phi_5 \\
\end{aligned}と表されます。
辺の長さを考えなくて良くなりましたが、ここで重要なのは、これらの二等辺三角形をすべて集めると、もともとの五芒星を構成し、かつ、各三角形の重なりは中央の五角形 B_1 B_2 B_3 B_4 B_5 だけであって、しかも重なりの回数は2回であることです。
すなわち、
\begin{aligned}
& \triangle A_1OA_3 + \triangle A_2OA_4 + \triangle A_3OA_5 \\
&+ \triangle A_4OA_1 + \triangle A_5OA_2 \\
= & \frac{1}2 \sum_{i=1}^5 \sin \phi_i\\
= & S
\end{aligned}が成り立ちます(図3)。
面積 S を中心角だけですっきりと表すことが出来ました。わざわざ T を2回足していたのは、正にこのためとしか思えません。