垂心を知っていれば解ける！解けるぞ！！ – 2023年京大 特色入試 数学 第1問

2023年8月2日2024年9月9日

　2023年京大 特色入試 数学 第1問 は平面図形の問題ですが、垂心というものを知っていれば、三角関数や微積分やその他の面倒な計算をせずに解くことが出来ます。問題文は以下のとおりです。

　何を言っているのか、今ひとつピンときませんが、順次見ていきましょう。

2023年京大 特色入試 数学 第1問 の解法

問題文の同一円周は △ABC の外接円

　 △ABC の頂点 A,B,C が同一円周上にあると言っているのですから、その円は正に △ABC の外接円です。外心を O と置きます。また、外接円の半径を r と置きます。

　 P が △ABC 内のどこにあれば D,E,F が外接円上に乗るかですが、 △ABC が正三角形の場合、 P が外心 O の位置にあれば、確かに D,E,F は外接円上にあります(図１)。

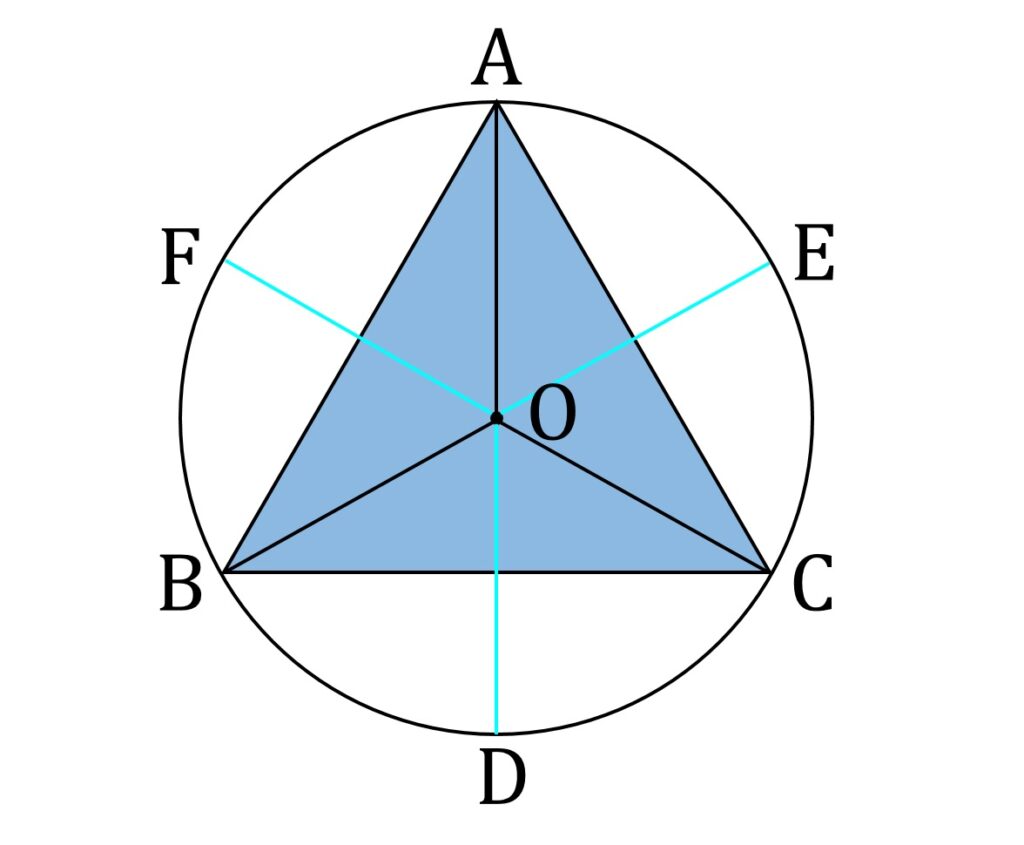
P が O 以外の場所にあるときは、D,E,F のすべてが外接円上にあるということは無さそうなので、 P は有っても２，３個（該当する P は存在しない場合もあるかも）と予想できます。

点 D が外接円周上に存在するとき、 P はどういう軌跡を採るか考える

　 D,E,F すべてを同時に考えるのは難しそうなので、まず点 D にフィーチャーします。

　点 D と点 P は辺BC を挟んで対象な位置に存在しているので、 辺 BC を挟んで外心 O と対象な点を O₁ と置くとき、D が外接円 O 上の弧 \stackrel{\huge\frown}{\mathrm{BC}} を動くならば、点 P は O₁ を中心とする半径 r の円周上でかつ、△ ABC 内の部分を動きます(図２)。

題意を満たす点 P が存在するための必要十分条件を求める

　同様に、辺 CA を挟んで外心 O と対象な点を O₂ 、辺 AB を挟んで外心 O と対象な点を O₃ と置くとき、点 P は O₂ を中心とする半径 r の円周上、および O₃ を中心とする半径 r の円周上、かつ△ ABC 内の部分を動きます。

　すなわち、題意を満たす点 P が存在するための必要条件は、円 O₁,O₂,O₃ が1点で交わり、かつその交点が△ ABC 内に存在することです(図３)。

　このような点 P が存在するとき、

 \mathrm{O_1 P } =  \mathrm{O_2 P } =  \mathrm{O_3 P } =r

ですが、これはすなわち、点 P は △O₁O₂O₃ の外心であり、かつ △O₁O₂O₃の外接円の半径が r であるということと同値です。したがって、題意を満たす点 P が存在するための必要条件は、△O₁O₂O₃ の外接円の半径が r であり、かつ外心が △ABC 内に存在することです(図４)。

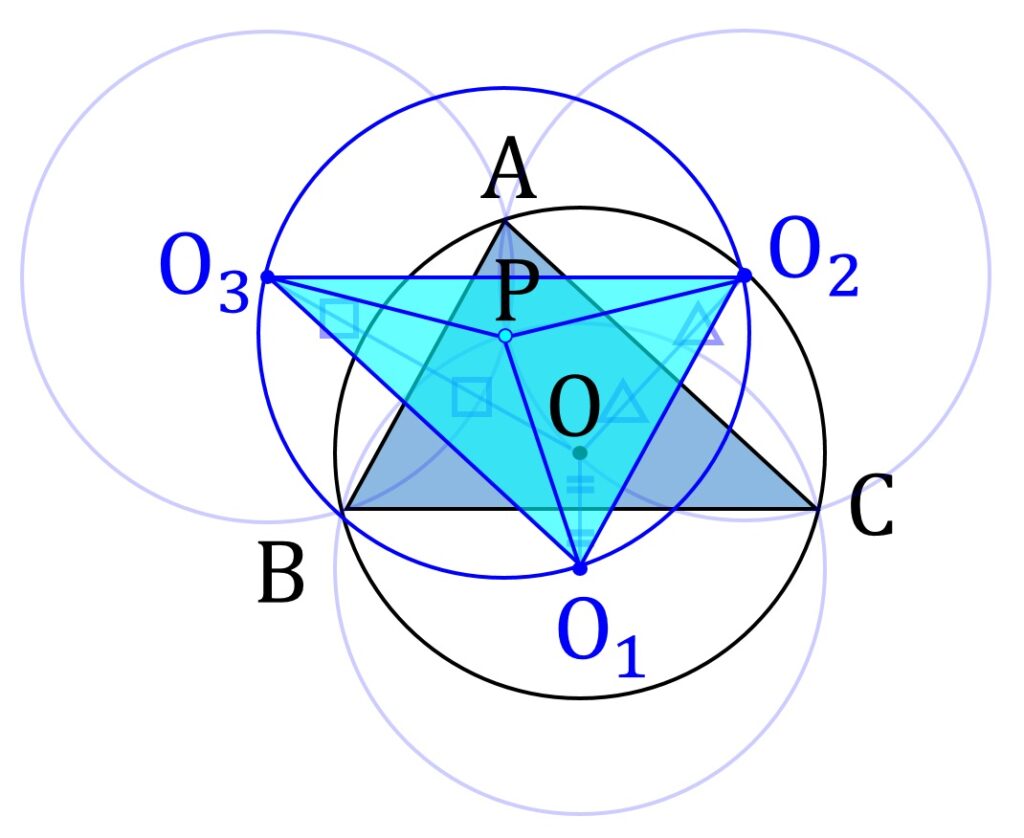
　また、これの十分性は明らかです。ゆえに、

題意を満たす点 P が存在するための必要十分条件は、△O₁O₂O₃ の外接円の半径が r であり、かつ外心が △ABC 内に存在することである

ことがわかりました。

　ここまでの議論により、題意を満たす点 P の個数は、高々1個であることがわかります。

題意を満たす点 P が1つだけ存在することを証明する

　導出した、題意を満たす点 P が存在するための必要十分条件「△O₁O₂O₃ の外接円の半径が r であり、かつ外心が △ABC 内に存在することである」がどのようなときに成立するのか、調べます。

　最初は △ABC の辺や角に適当な記号を振って、△O₁O₂O₃ の外接円半径をそれらで表し、それが r に等しいという式を立てようとしました。

　先に、 △ABC が正三角形の場合は存在することを示したので、△ABC が二等辺三角形なら必要十分条件が成立し、そうでなければ題意を満たす P は存在しない、みたいな結果が出ることを予想したのですが、計算が複雑になりすぎてうんざりしてしまいました。別のもっと楽なアプローチを模索します。

　ここで、各辺 BC,CA,AB が線分 O₁P,O₂P,O₃P をそれぞれ2等分することに着目します。 O₁P,O₂P,O₃P の中点をそれぞれ H,I,J と置くとき、 H,I,J はそれぞれ辺 BC,CA,AB 上の点ですが、それらは各々 BC,CA,AB の中点でも有ります。

　三角形の各辺の中点が現れたら、本能的にそれらを結んでみたくなるものです(図５)。

　そうやって △HIJ を描画してみると、以下のことがただちにわかります。

1. △HIJ ∽ △ABC、相似比は1:2
2. △HIJ ∽ △O₁O₂O₃ 、相似比は1:2
3. △ABC の外心は △O₁O₂O₃ の垂心である

　①および②は明らかです。高校入試じゃないので、証明は不要でしょう。

　③は AB // O₁O₂ // HI , BC // O₂O₃ // IJ , CA // O₁O₃ // HJ であることから、直線 O₃O , O₂O, O₁O がそれぞれ O₁O₂,O₂O₃,O₁O₃ と直交するので、明らかです(図６)。

　①および②から、 △ABC ≡ △O₁O₂O₃ がただちに導き出せます。よって△O₁O₂O₃ の外接円の半径は △ABC と同じ r です。

　残りは△O₁O₂O₃ の外心が △ABC の内部に存在していることの証明です。ここで条件③が生きてきます。

　 △ABC の外心が △O₁O₂O₃ の垂心なら、図形の対称性から見て △O₁O₂O₃ の外心も △ABC の垂心になっていそうです。実際、 △ABC の頂点 A から辺 BC に垂らした垂線は△O₁O₂O₃ の辺 O₂O₃ と直交しますが、一方で△AOO₃ は AJ がOO₃ を垂直二等分するので二等辺三角形であり、 AO = AO₃ = r です。同様に △AOO₂ は二等辺三角形であり、 AO = AO₂ = r です。したがって AO₂ = AO₃ = r なので △AO₂O₃ は二等辺三角形であり、頂点 A から辺 BC に垂らした垂線は辺 O₂O₃ を垂直二等分します(図７)。

　頂点 B および C についても同様のことが言えるので、 △ABC の垂心 が △O₁O₂O₃ の外心であることが示せました。

　 △ABC は鋭角三角形なので、垂心は三角形の内部に有ります。よって △O₁O₂O₃ の外心も △ABC の内部です。

　ゆえに、題意を満たす P は１つ存在し、それは△ABC の垂心であることが証明できました。

解法のポイント

　点 P に求められる必要条件から、円 O₁ , O₂ , O₃ を考慮する必要性に気付くことが、死活的に重要です。これがないと本問の攻略は厳しいでしょう。この点に関しては、本問は図形の線対称に関する問題のバリエーションなので、そのことに気づけば突破できるでしょう。

　ここから、 P が存在すればそれは △O₁O₂O₃ の外心であるということに気づくのは、外心の定義から容易であると思います。これに比べると、 △O₁O₂O₃ の外接円の半径が △ABC と等しいことを証明するのは、かなりハードルが高くなります。

　これについては本稿で示したように、△ABC ≡ △O₁O₂O₃ を証明することが近道です。図形の問題で中点が出てきたらそれらを結んでみよう、というのは高校入試での鉄則ですが、これは大学入試でも同じです。高校に行くと三角関数とか便利なツールが出てきますが、中学時代の基本動作も重要なので、忘れないようにしましょう。結構助けられる局面が有ります。

　最後に、△O₁O₂O₃ の外心が △ABC の内部にあることの証明ですが、意外なことにこれが一番大変です。ここで垂心というものを思い出せるかどうかで、明暗が別れます。垂心なんて滅多に見かけませんが、教科書には「 △HIJ の垂心が △ABC の外心であることを証明せよ」（記号は本稿に準じる）などという、本問ですぐさま使えそうな練習問題が載っていたりします。

　教科書には時々、思いの外アドバンスドな内容がしれっと書いてあったりするので、受験には関係ないや的にお座なりにせず、普段からしっかり勉強するようにしましょう。

　また、本稿で見たとおり、外心と垂心は親和性があるので、これを機会に理解を深めておきましょう。