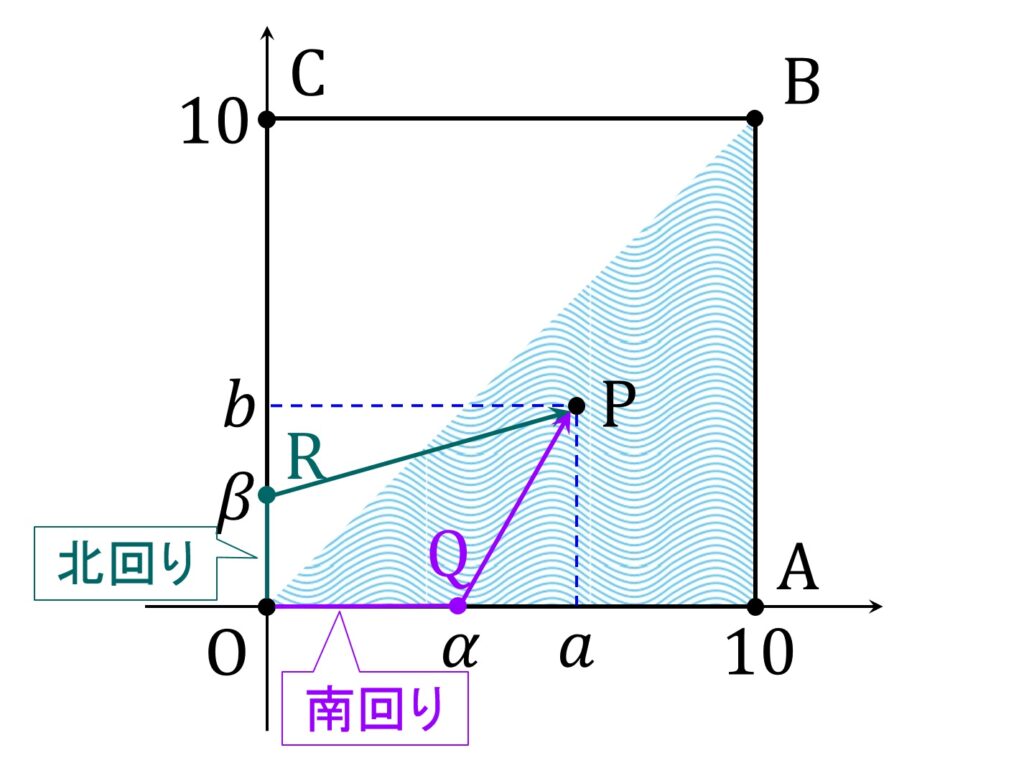
点Pへの最短経路
点 P に到る経路としては、辺 OA 経由の「南回り」ルートと辺 OC 経由の「北回り」ルートが考えられます。北回りルートのほうが水の中にいる距離が長いので、明らかに南回りのほうが所要時間が短くなります(図3)。
と言い切ってしまいたいですが、これはそれほど自明ではありません。とは言え、感覚的には南回りのほうが速そうなので、まずこちらのルートの所要時間を計算します。
監視員は原点 O を出発して辺 OA 上の点 Q( α,0 ) ( 0 ≦ α ≦ a ) までプールサイドを移動し、点 Q からプールに入って点 P まで直線状に移動するものとします。
このとき、所要時間 f(α) は
f( \alpha) = \frac{ \alpha}2 + \sqrt{(a - \alpha)^2 + b^2}で与えられます。
α を動かしてこれの最小値を求めると、それが南回りの最短時間となります。
そこで f(α) を微分します。
\begin{aligned}
f'( \alpha) & = \frac{ 1}2 -\frac{ a - \alpha}{ \sqrt{(a - \alpha)^2 + b^2}} \\
& = \frac{ 1}2 -\frac{ 1}{ \sqrt{ 1 + ( \frac{b}{a- \alpha})^2}} \\
\end{aligned}なので、 f'(α) は α の単調増加関数であることがわかります。また、 f‘(a) > 0 です。 f‘(0) の符号がどうなっているかですが、 b ≦ a なので
\begin{aligned}
f'( 0) & = \frac{ 1}2 -\frac{ 1}{ \sqrt{ 1 + ( \frac{b}{a})^2}} \\
& \leqq \frac{ 1}2 - \frac{ 1}{ \sqrt{2}} <0
\end{aligned}です。
したがって f(α) は、α が f‘(α) = 0 を満たすときに最小値を取ります。
\begin{aligned}
f'( \alpha) & = \frac{ 1}2 -\frac{ a - \alpha}{ \sqrt{(a - \alpha)^2 + b^2}}=0 \\
\end{aligned}のとき、
\begin{aligned}
\frac{ a - \alpha}{ \sqrt{(a - \alpha)^2 + b^2}}= \frac{ 1}2 \\
\end{aligned}なので両辺を2乗して
\begin{aligned}
\frac{ (a - \alpha) ^2}{ (a - \alpha)^2 + b^2}= \frac{ 1}4 \\
\end{aligned}分母を払って
\begin{aligned}
4(a - \alpha) ^2= (a - \alpha)^2 + b^2 \\
\end{aligned}よって
\begin{aligned}
3(a - \alpha) ^2= b^2 \\
\end{aligned}なので、 0 ≦ α ≦ a であることから
\alpha = a - \frac{b} { \sqrt{3}}です。
したがって南回りルートの最短時間は
\begin{aligned}
& f( a - \frac{b} { \sqrt{3}}) \\
= & \frac{1}2 \left ( a - \frac{b} { \sqrt{3}} \right ) + \sqrt{ \left (a - a + \frac{b}{\sqrt{3}} \right)^2 + b^2} \\
= & \frac{a}2 -\frac{b} { 2\sqrt{3}} + \frac{2b}{\sqrt{3}} \\
= & \frac{a}2 + \frac{(-1 +4)b} { 2\sqrt{3}} \\
= & \frac{a + \sqrt{3} b}2
\end{aligned}です。
次に北回りルートの最短時間を求めます。
監視員は原点 O を出発して辺 OC上の点 R( 0,β ) ( 0 ≦ β ≦ b ) までプールサイドを移動し、点 R からプールに入って点 P まで直線状に移動するものとします。
このとき、所要時間 g(β) は
g( \beta) = \frac{ \beta}2 + \sqrt{a^2 +( b - \beta)^2}で与えられます。
これを β で微分して
\begin{aligned}
g'( \beta) & = \frac{ 1}2 -\frac{ b - \beta}{ \sqrt{a^2 +(b - \beta)^2 }} \\
& = \frac{ 1}2 -\frac{ 1}{ \sqrt{ 1 + ( \frac{a}{b- \beta})^2}} \\
\end{aligned}ですが、 g‘(β) は単調増加関数であり、g‘(b) > 0 です。g‘(0) の評価はちょっと面倒くさくて、
\begin{aligned}
g'( 0) & = \frac{ 1}2 -\frac{ 1}{ \sqrt{ 1 + ( \frac{a}{b})^2}} \\
\end{aligned}は \displaystyle\frac{a}{\sqrt{3}} \leqq b \leqq a のとき g'(0) ≦ 0 、 0 \leqq b < \displaystyle\frac{a}{\sqrt{3}} のとき g'(0) > 0 です。
したがって g(β) は \displaystyle\frac{a}{\sqrt{3}} \leqq b \leqq a のとき、南回りルートの場合と同じ計算方法により、
\beta = b - \frac{a} { \sqrt{3}}のときに最小値
\frac{b + \sqrt{3} a}2をとります。また 0 \leqq b < \displaystyle\frac{a}{\sqrt{3}} のとき、最小値
g( 0) = \sqrt{a^2 + b ^2}をとります。
以上の結果を元に、南回りルートのほうが速いことを証明します。
まず \displaystyle\frac{a}{\sqrt{3}} \leqq b \leqq a のとき、
\frac{b + \sqrt{3} a}2 - \frac{a + \sqrt{3} b}2 = \frac{( \sqrt{3} -1)(a-b)}2 \geqq 0 なので、南回りルートの勝ちです。
また 0 \leqq b < \displaystyle\frac{a}{\sqrt{3}} のとき、北回りルートは原点 O からプール内を直接 P に向かうルートが最短ですが、これより南回りルートのほうが速いのは
\begin{aligned}
& f( a - \frac{b} { \sqrt{3}}) < f(0) = g(0)\\
\end{aligned}であることから明らかです。
以上、南回りルートのほうが速いことが証明できました。