向こう側のプールサイドから回り込むルートを考える
点 P がプールサイド AB に近づくと、プールサイドをぐるっと回り込んで、後ろ側のプールサイド AB からアプローチする「東回り」ルートのほうが時間が短縮できそうな気がします。
そこで、そのようなルートを取ったときの所要時間を求めます。
監視員は原点 O からて辺 OA 上を移動して頂点 A を経由し、辺AB 上の点 S( 10,β ) ( 0 ≦ β ≦ b ) までプールサイドを移動し、点 S からプールに入って点 P まで直線状に移動するものとします(図4)。
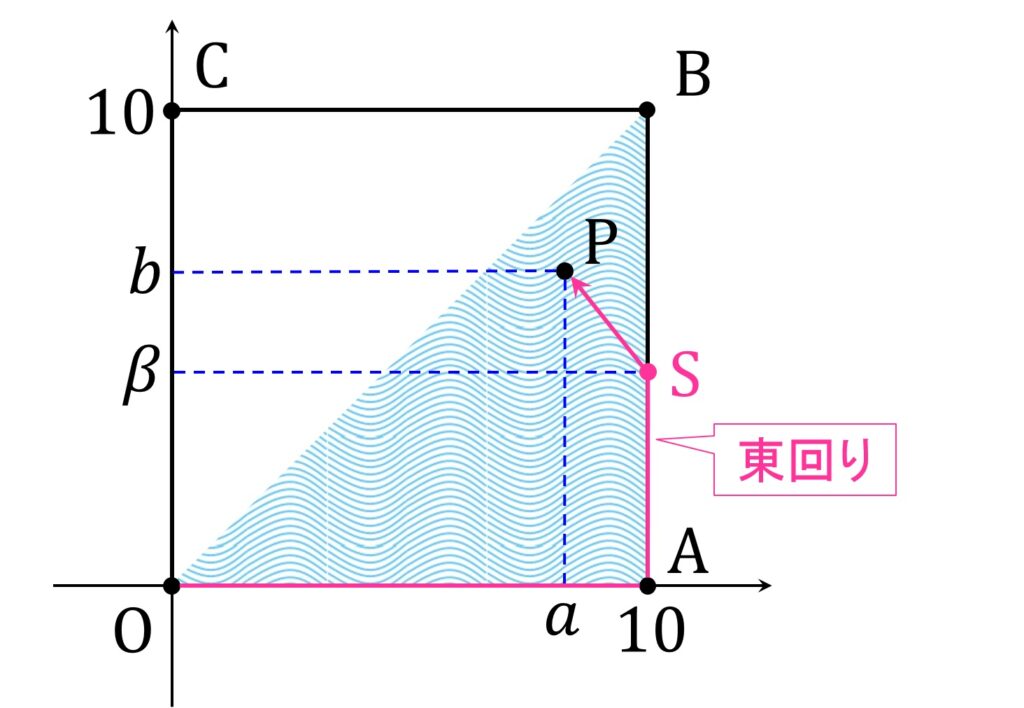
このとき、所要時間 h(β) は
h( \beta) =5+ \frac{ \beta}2 + \sqrt{(10-a )^2 + (b-\beta)^2}で与えられます。
これを β で微分して
\begin{aligned}
h'( \beta) & = \frac{ 1}2 -\frac{ b - \beta}{ \sqrt{(10-a)^2 +(b - \beta)^2 }} \\
& = \frac{ 1}2 -\frac{ 1}{ \sqrt{ 1 + ( \frac{10-a}{b- \beta})^2}} \\
\end{aligned}ですが、 h‘(β) は単調増加関数であり、h‘(b) > 0 です。また、
\begin{aligned}
h'( 0) & = \frac{ 1}2 -\frac{ 1}{ \sqrt{ 1 + ( \frac{10-a}{b})^2}} \\
\end{aligned}は \displaystyle\frac{10-a}{\sqrt{3}} \leqq b \leqq a のとき h‘(0) ≦ 0 、 0 \leqq b < \displaystyle\frac{10-a}{\sqrt{3}} のとき h‘(0) > 0 です。
したがって h(β) は \displaystyle\frac{10-a}{\sqrt{3}} \leqq b \leqq a のとき、
\beta = b - \frac{10-a} { \sqrt{3}}のときに最小値
\frac{b - \sqrt{3} a}2 + 5 (1+ \sqrt{3}) をとります。また 0 \leqq b < \displaystyle\frac{10-a}{\sqrt{3}} のとき、最小値
h( 0) = 5+ \sqrt{(10-a)^2 + b ^2}をとります。
こうして得られた東回り最小時間と、南回り最小時間の大小を比較します。
まず 0 \leqq b < \displaystyle\frac{10-a}{\sqrt{3}} の場合です。
\begin{aligned}
& 5+ \sqrt{(10-a)^2 + b ^2} - \frac{a + \sqrt{3} b}2 \\
\geqq & 5+ \sqrt{(10-a)^2 + b ^2} -\frac{a + \sqrt{3}\frac{10-a}{\sqrt{3}}}2 \\
= & 5+ \sqrt{(10-a)^2 + b ^2} -5 \\
= & \sqrt{(10-a)^2 + b ^2} > 0
\end{aligned}なので、南回りルートの勝ちです。
次に \displaystyle\frac{10-a}{\sqrt{3}} \leqq b \leqq a の場合です。
\begin{aligned}
& \frac{b - \sqrt{3} a}2 + 5 (1+ \sqrt{3}) - \frac{a + \sqrt{3} b}2 \\
= & \frac{(1 + \sqrt{3})(10-a)}{2} + \frac{1 - \sqrt{3}}{2} b
\end{aligned}なので、
\begin{aligned}
\frac{(1 + \sqrt{3})(10-a)}{2} + \frac{1 - \sqrt{3}}{2} b \geqq 0
\end{aligned}すなわち
\begin{aligned}
b \leqq \frac{(1 + \sqrt{3})^2}{2} (10-a)
\end{aligned}のとき、南回りルートのほうが速く到達します。また、
\begin{aligned}
\frac{(1 + \sqrt{3})(10-a)}{2} + \frac{1 - \sqrt{3}}{2} b < 0
\end{aligned}すなわち
\begin{aligned}
b > \frac{(1 + \sqrt{3})^2}{2} (10-a)
\end{aligned}のとき、東回りルートのほうが速く到達します。
\frac{1}{ \sqrt{3}} < \frac{(1 + \sqrt{3})^2}{2}なので、 0 ≦ a ≦ 10 の範囲において 0 \leqq b < \displaystyle\frac{10-a}{\sqrt{3}} ならば b \leqq \displaystyle\frac{(1 + \sqrt{3})^2}{2} (10-a) です。よって最短ルートが南回りか東回りかの境界線は
\begin{aligned}
y = \frac{(1 + \sqrt{3})^2}{2} (10-x)
\end{aligned}のみです(すなわち、 0 \leqq b < \displaystyle\frac{10-a}{\sqrt{3}} か \displaystyle\frac{10-a}{\sqrt{3}} \leqq b \leqq a かどうかは考えなくて良い)(図5)。
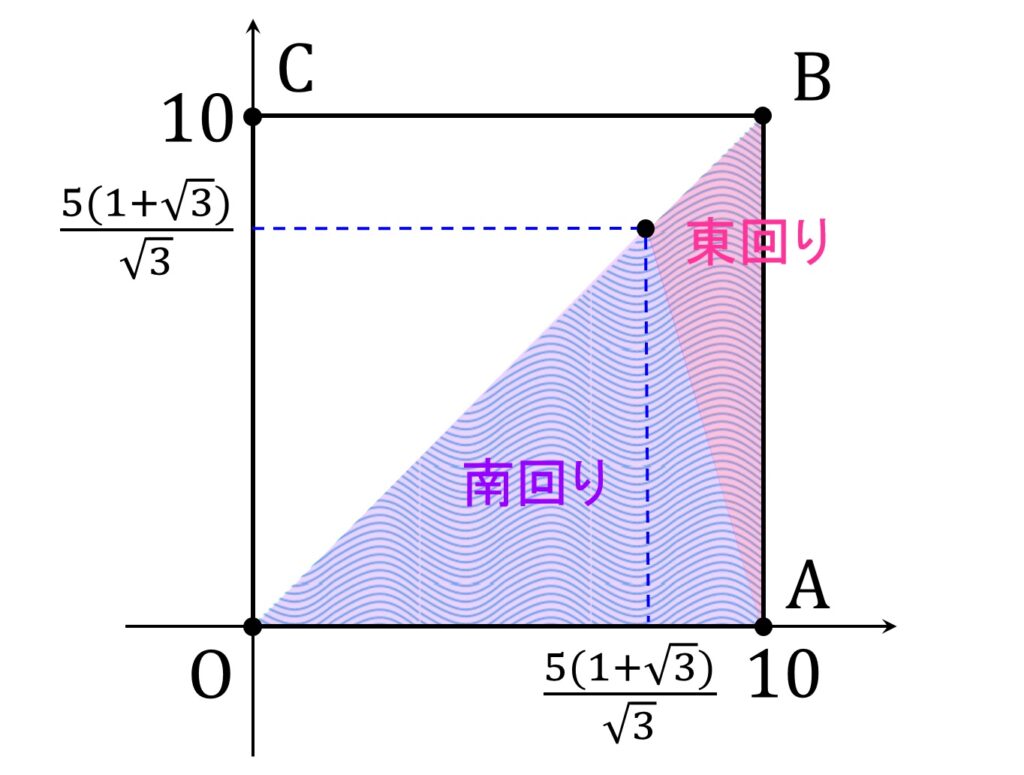
ゆえに最短ルートが東回りのとき、所要時間は
\frac{b - \sqrt{3} a}2 + 5 (1+ \sqrt{3}) です。