式で書くと至極当然で、むしろなんか間抜けな感じがしますが、これが図形分野では無類の強さを発揮します。
角度問題への適用
図形の問題で2つの角度が等しいことを示せと言われたとき、よく使う道具は平行線の同位角や錯角、対頂角、三角形の合同や相似、などですが、それに加えてこの「a + 5 = b + 5 なら a = b」です。具体的には以下の図1のようなケースです。

図で示されると「確かに!」と思いますが、結構気が付きにくいので図形問題で多用されています。
隣り合う角だけでなく、離れたところにある角に対しても応用できます。例えば以下の図2の場合です。
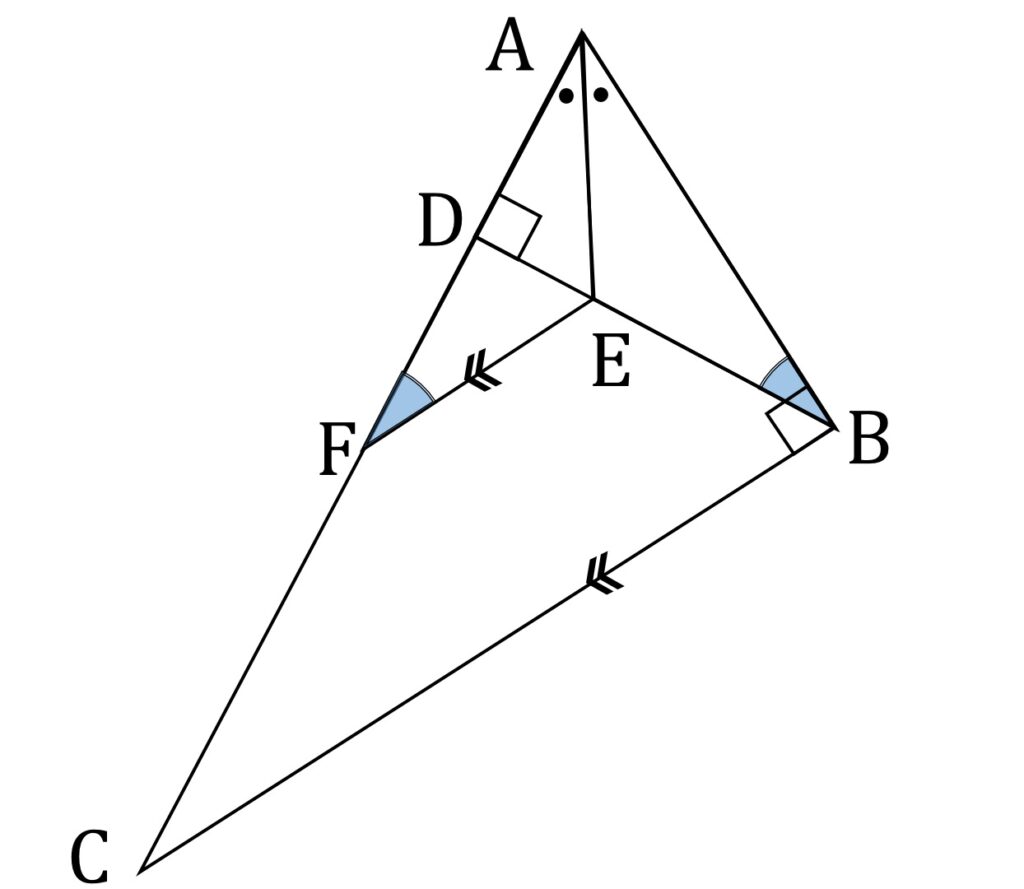
図2において、直角三角形 △ABC の頂点 B から辺 AC に垂らした垂線の足を D 、∠BAC の二等分線と BD の交点を E 、 E を通り BC と平行な直線と AC との交点を F とします。
以上の条件の下で ∠DFE = ∠ABE を証明したいのですが、まず EF // BC なので
\angle \mathrm{DFE} = \angle \mathrm{ACB}です。 ここで ∠ACB と ∠ABD に対し、「a + 5 = b + 5 なら a = b」技法を適用します。
△ABC は直角三角形なので
\angle \mathrm{ACB} + \angle \mathrm{BAC} = 90 ^{ \circ}です。一方 △ABD も直角三角形なので
\angle \mathrm{ABD} + \angle \mathrm{BAD} = 90 ^{ \circ}です。したがって
\angle \mathrm{ACB} + \angle \mathrm{BAC} =\angle \mathrm{ABD} + \angle \mathrm{BAD} ですが、 ∠BAC と ∠BAD は同じものなので
\angle \mathrm{ACB} =\angle \mathrm{ABD} です。さらに ∠ABD と ∠ABE も同じものなので
\angle \mathrm{DFE} = \angle \mathrm{ACB} =\angle \mathrm{ABD} =\angle \mathrm{ABE} が成り立ちます。
面積問題への適用
2つの図形の面積が等しいことを証明する場合にも「a + 5 = b + 5 なら a = b」技法が役に立ちます。例えば以下のような場合です。

図3において、傾き - \displaystyle\frac{1}2 の直線 l を動かして □BCDE と △AEF の面積が等しくなるようにしたときの b の値を求めたいとき、各辺の長さを b で表して面積が等しくなるように方程式を立てようとすると、計算が面倒くさくてうんざりします。
ここで「a + 5 = b + 5 なら a = b」技法の出番です。
□BCDE + □AEDO = □ABCO
△AEF + □AEDO = △FDO
なので、
□ABCO = △FDO
が成り立てば
□BCDE + □AEDO = △AEF + □AEDO
であり、
□BCDE = △AEF
が成り立ちます。
□ABCO = 60
△FDO = b2
なので、求める b は
b^2 = 60
すなわち
b = 2 \sqrt{15}です。
図形問題で行き詰ったら「a + 5 = b + 5 なら a = b」

難しい問題ほど難易度を上げるため「a + 5 = b + 5 なら a = b」技法を前提とした出題になっています。角度や面積を評価する問題でにっちもさっちもいかなくなったときは、「a + 5 = b + 5 なら a = b」技法が使えないか検討してみましょう。
成績UPを目指すなら峰企画の数学家庭教師
「成績が伸び悩んている」「授業についていけない」といった場合は、当社家庭教師にお気軽にご相談ください。無料の体験授業実施中です。中学生なら理科の授業も受け付けています。
