1997年東大 数学 第4問 小問2の解法
小問1で見たように、第1列のどの頂点も \tan \theta = \displaystyle\frac{ \sqrt{3}} { \text{奇数}} となってしまうので、第2列から候補を探します。
すると、小問1と同様に求める鏡像頂点が直ちに見つかります(図8)。
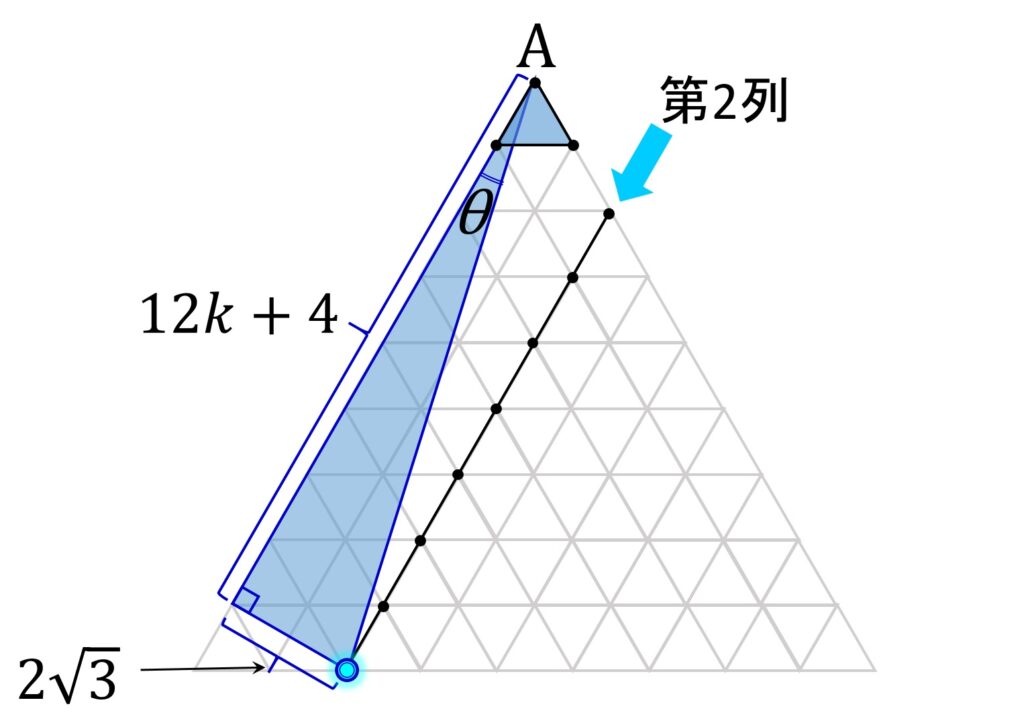
図8の直角三角形の辺のうち、元の三角形の辺 AB に沿った辺の長さは 12k+4 ですが、元の三角形の1辺の長さを2と置いているので、含まれる辺の個数は 6k+2 です。したがって含まれる頂点のうち、出発点のAを除く数も 6k+2 です。
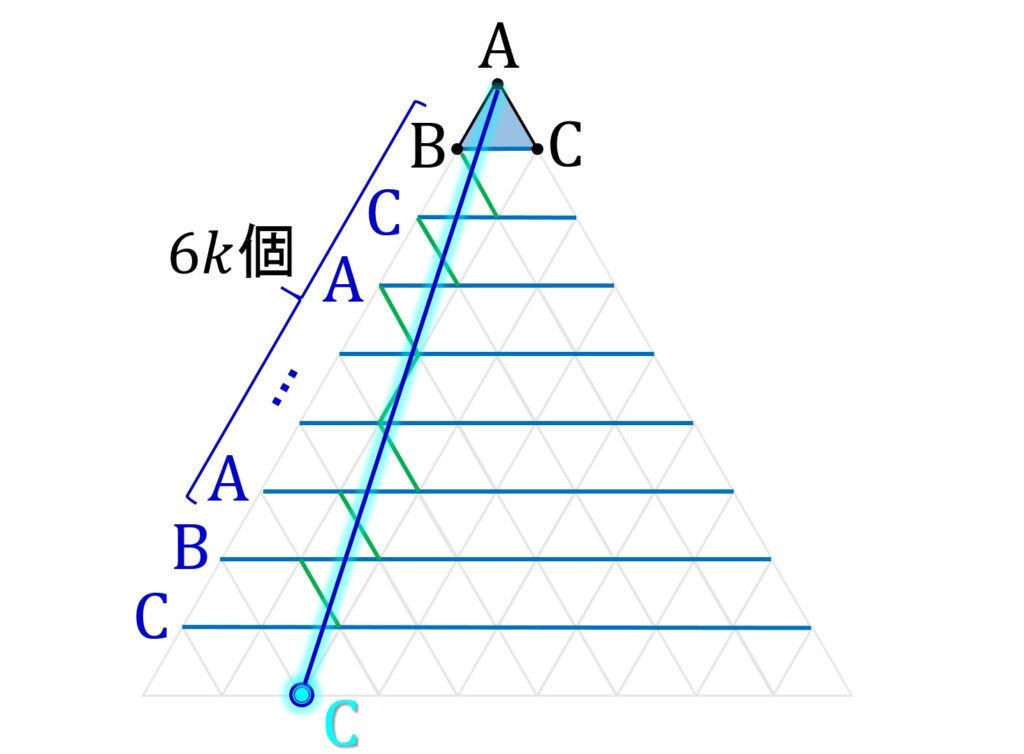
鏡像頂点の並びは3つごとに一巡します。したがってもとの頂点 A から見て 6k+2 個先の頂点は C です。目的の鏡像頂点はこれと鏡像関係にあるのでやはり C です(図9)。

反射の回数は、出発点のA と 終点の鏡像 C を結ぶ線分が鏡像面と交差する回数です。
鏡像面には BC と平行なものと、 AB または AC と平行な(要は「斜め」な)ものの2種類があります。 BC に平行な鏡像面の個数は直線 AB 上の頂点の数と同じで 6k+2 個です。斜めの鏡像面は平行鏡像面の間に1個ずつあるので、その数は 6k+1 個です(図10)。
ゆえに反射の回数は 12k+3 回です。
解法のポイント

本問は鏡像の問題だというところから、図2が描ければ何とかなります。「光の反射」とか「跳ね返って最短」的な問題は小学校や中学校では見かけることもありましたが、この機会に思い出しておきましょう。