2002年京大 後期 数学 第3問 は四面体の正射影に関する難問です。問題文は以下のとおりです。
各面が鋭角三角形からなる四面体 ABCD において,辺 AB と辺 CD は垂直ではないとする.このとき辺 AB を含む平面 α に点 C,点 D から下ろした垂線の足をそれぞれ C’ , D’ するとき,4 点 A,B,C’,D’ がすべて相異なり,しかも同一円周上にあるように α がとれることを示せ.
四面体の正射影に関する問題は過去にありましたが(1988年東大 数学 第2問など)、本問のように正射影の四角形が円に内接するようにしろというのはなかなかにエクストリームで、ちょっと思い当たりません。どうすればいいのか見当もつかない危険極まりない問題です。とっとと見切りをつけて、もっと何とかなりそうな問題に着手するのが正しい判断と言えるでしょう。
それでは解き方を見ていきます。
まず頭の中で問題文の意味するところをイメージする
まずは検討の足がかりを築いて、原初の混沌状態からの脱却を図ります。
射影面 α は AB を含むので、 α を AB を軸に回転させて、正射影が円に内接するようにすれば良いということがわかります。
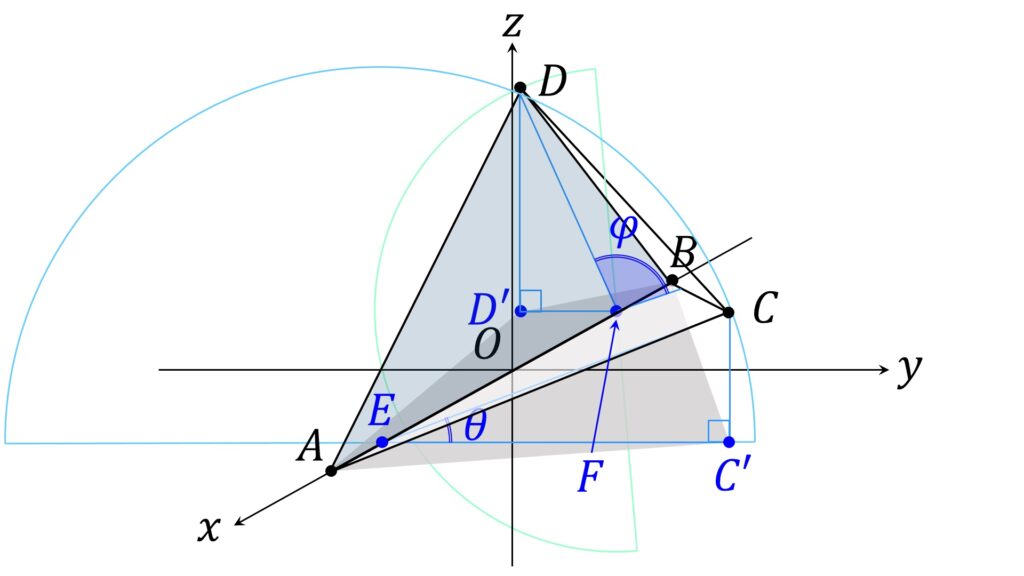
頭の中で α をぐるぐる回転させているうちに、 C’ や D’ はそれぞれ AB に垂直な平面上に常にいるんじゃないかという気がしてくれば、まずは最初の橋頭堡確保が成功です(図1)。
実際、 C および D から直線 AB に下ろした垂線の足をそれぞれ E , F とおくとき、 \overrightarrow{CE} \perp \overrightarrow{AB} かつ、 CC’ は α に垂直なので当然 \overrightarrow{CC'} \perp \overrightarrow{AB} です。したがって \overrightarrow{CE} , \overrightarrow{CC'} で張られる平面は常に AB と垂直です。すなわち C’ は常に E を通り AB に垂直な平面上にあります。同様に、D’ は常に F を通り AB に垂直な平面上にあります。
なお、辺 AB と辺 CD は垂直ではないので、2つの平面は一致しません。
問題文の内容を定式化する
次に、問題文の内容を数学で扱えるように定式化します。
平面 α をぐるぐる回すのは頭の体操的にしんどいので、 α は xy 平面として固定し AB を x 軸上に置いて、 C および D を x 軸を中心として回転させることにします。
A,B の座標をそれぞれ (1,0,0) , (-1,0,0) とします。四面体 ABCD は各面がすべて鋭角三角形なので、 E および F は A,B の間にあります(つまり x 座標の絶対値が 1 未満)。もし E が線分 AB の「外側」にあると、 △ABC は鈍角三角形になってしまうからです。 F についても同様です。
E, F の x 座標をそれぞれ p,q とおきます。 -1 < q < p < 1 であるとして一般性を失いません(もし逆なら、 A と B を入れ替えればよい)。このとき
\begin{aligned}
& C(p,CE \cos \theta, CE \sin \theta) \\
& D(q,DF\cos( \theta + \phi), DF \sin ( \theta + \phi) ) \\
& C'(p,CE \cos \theta, 0) \\
& D'(q,DF \cos( \theta + \phi), 0 ) \\
& E(p,0,0) \\
& F(q,0,0) \\
\end{aligned}
です。ここに 0 ≦ θ ≦ π は平面 α の回転角です。 α が△ABC に一致するところから始めて、α を頂点 A から見て時計回りに半回転( すなわち C ,D を反時計回りに半回転)させるイメージです。
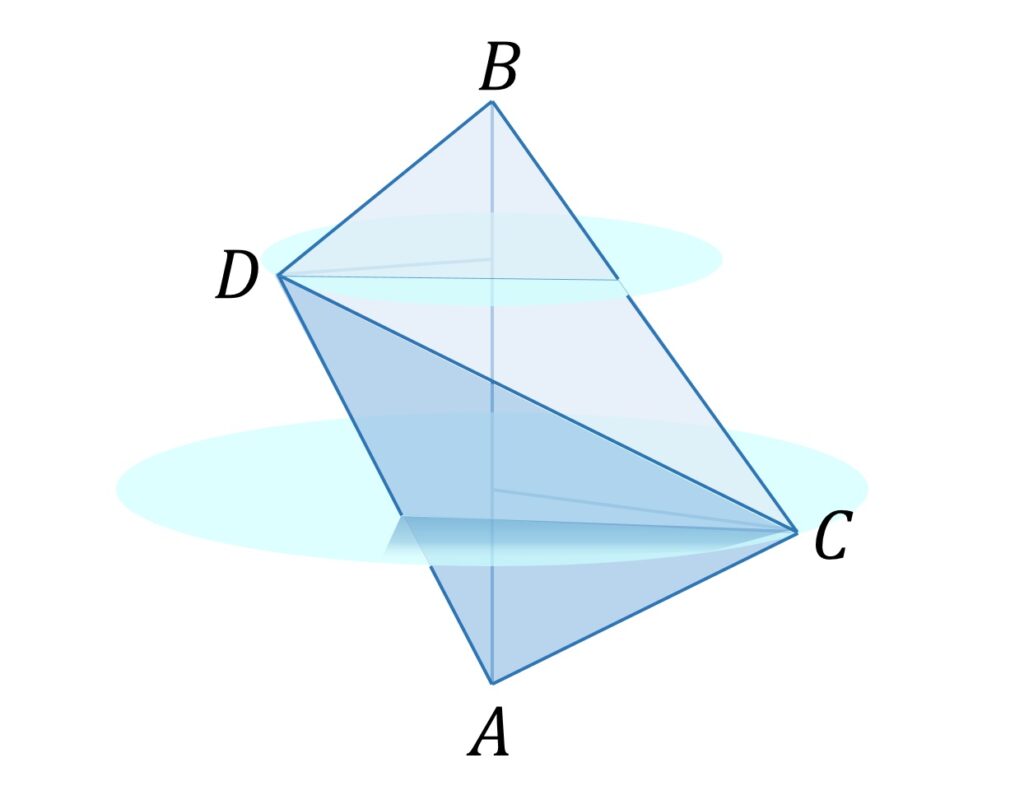
また 0 < φ < π は △ABC と △ABD の成す角です。 A から見て C,D を反時計回りに回転させるときに、 A の方が先行していると φ は負の値になるべきなのですが、その場合はABに平行な平面を対象面とする鏡像を考えることにより、 φ は正であるとして一般性を失いません(図2)。