四面体正射影の激難問 – 2002年京大 後期 数学 第3問

2025年1月14日2025年1月16日

円周角と中間値の定理を使って証明する

　だいぶ数学っぽくなってきました。以上の準備のもとで四角形 ABC’D’ が円に内接する条件を考えますが、やはり円周角で勝負するのが良さそうです。

　角度が θ の連続関数なので、中間値の定理によって対応する角が等しくなる θ₀ が存在する、といったことを示す方向で攻めます。角度の連続性は後で証明します。

　ところが、 C’,D’ が AB の片側に集まっているか左右に散っているかで、対応する角が変わってきます。まったく頭が沸きそうですが、とりあえず 0 \leqq \theta < \displaystyle\frac{\pi}2 の範囲で考えてみます。

　この場合、 φ の大きさによって D’ が C’ と同じ側にいるのか反対側にいるのかが変わってくる上に、 \theta = 0 や \theta = \displaystyle\frac{\pi}2 のときに比較対象の角のどちらが大きいのかの判定も難しく、面倒臭さMAXです(図3)。

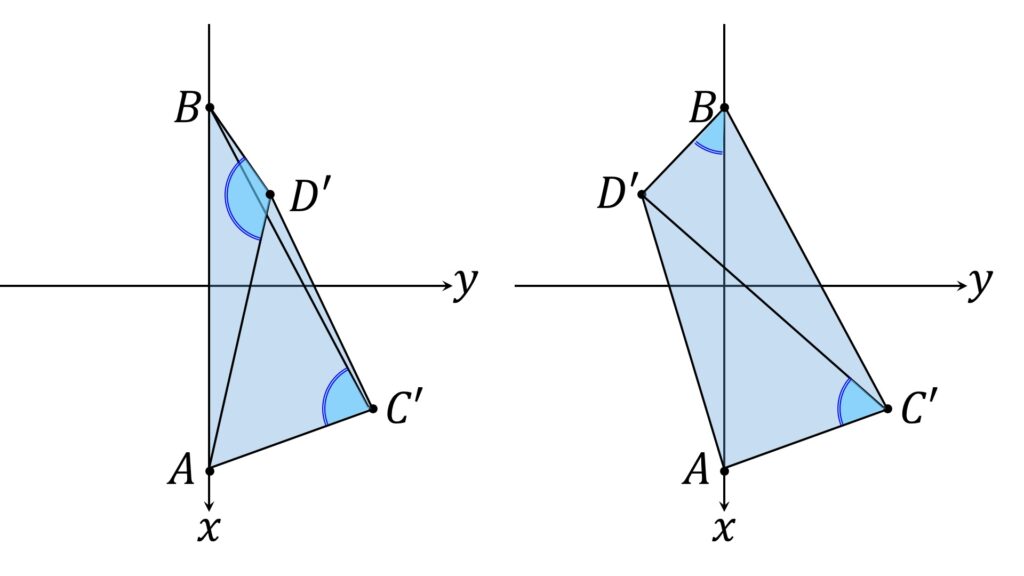
　一方 \displaystyle\frac{\pi}2 \leqq \theta \leqq \displaystyle\frac{3\pi}2 - \phi の場合、 C’ も D’ も辺ABの「左側」（ xy 平面の y ≦ 0 の領域）に存在します(図4)。

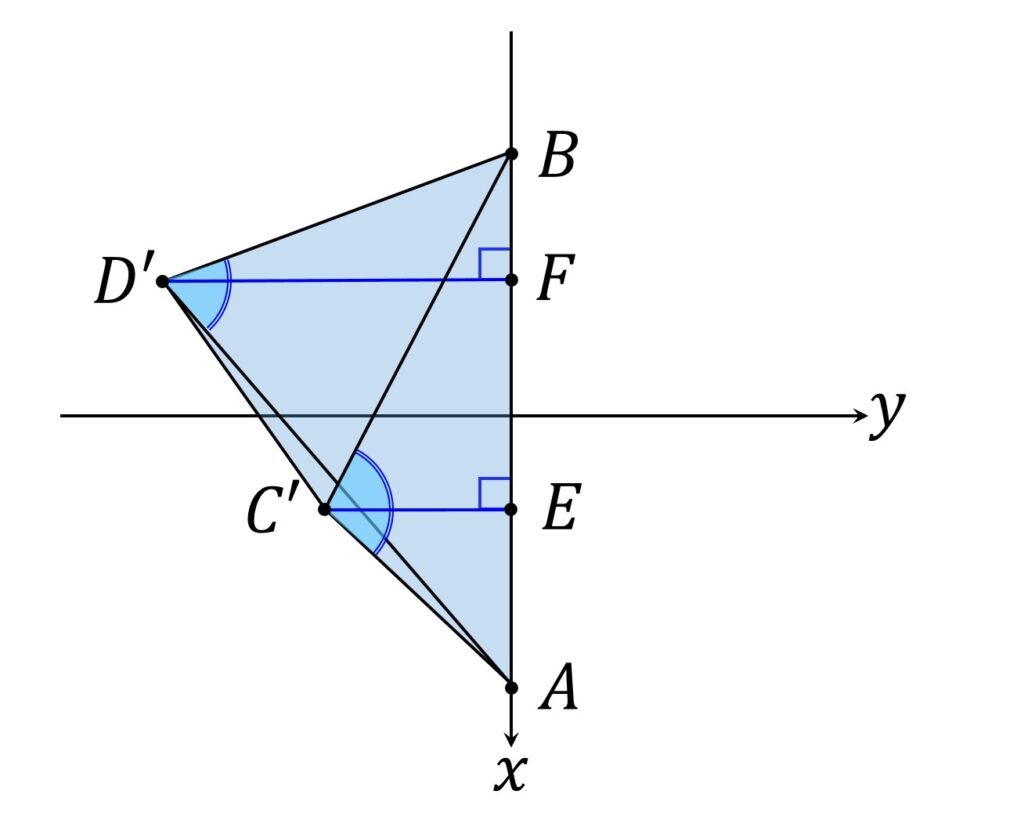
　比較対象の2角

 \begin{aligned}
 & a = \angle AC'B \\
 & b = \angle AD'B
\end{aligned}

は \theta =\displaystyle\frac{\pi}2 のとき C’ は AB 上に存在しますが D’ はそうでないので

 \begin{aligned}
 & a =  \pi\\
 & b < \pi 
\end{aligned}

です。また \theta =\displaystyle\frac{3\pi}2 - \phi のとき D’ は AB 上に存在しますが C’ はそうでないので

 \begin{aligned}
 & a <  \pi\\
 & b = \pi 
\end{aligned}

です。

　 a,b は明らかに θ の連続関数です。

\begin{aligned}
AC'  & = \sqrt{AE^2 + C'E^2 } \\
  & =  \sqrt{AE^2 + CE^2 \cos ^2 \theta } \\
BC'  & = \sqrt{BE^2 + C'E^2 } \\
  & =  \sqrt{BE^2 + CE^2 \cos ^2 \theta } \\
\end{aligned}

なので AC’, BC’ はいずれも θ の連続関数です。したがって

a = \arccos( \frac{AC'^2 + BC'^2 - AB^2}{2 AC' \cdot BC'})

も θ の連続関数です。同様に b も θ の連続関数です。

　ゆえに中間値の定理によりある \displaystyle\frac{\pi}2 < \theta_0 < \displaystyle\frac{3\pi}2 - \phi が存在して、θ = θ₀ のとき

a=b

です。

　と言いたいところですが、高校の範囲で arccos は出てこないし、そもそも逆関数の連続性も範囲外っぽいです。そこで角度 a や b を直接扱うのではなく、 cos a と cos b を θ の関数と見立てて、これらに中間値の定理を適用します。

 \cos a = \frac{AC'^2 + BC'^2 - AB^2}{2 AC' \cdot BC'}

なので cos a は θ の連続関数です。同様に cos b も θ の連続関数です。

　 \theta =\displaystyle\frac{\pi}2 のとき

 \begin{aligned}
 &  \cos a =   -1\\
 & \cos b >  -1 
\end{aligned}

\theta =\displaystyle\frac{3\pi}2 - \phi のとき

 \begin{aligned}
 &  \cos a  > -1 \\
 & \cos  b = -1  
\end{aligned}

なので、中間値の定理によりある \displaystyle\frac{\pi}2 < \theta_0 < \displaystyle\frac{3\pi}2 - \phi が存在して、θ = θ₀ のとき

 \cos a= \cos b

です。

　明らかに 0 < a,b ≦ π ですが、この範囲で cos a, cos b は単調減少関数です。ゆえに a = b すなわち

 \begin{aligned}
  \angle AC'B =  \angle AD'B
\end{aligned}

が成り立ち、このとき四角形 ABC’D’ は円に内接します(図5)。

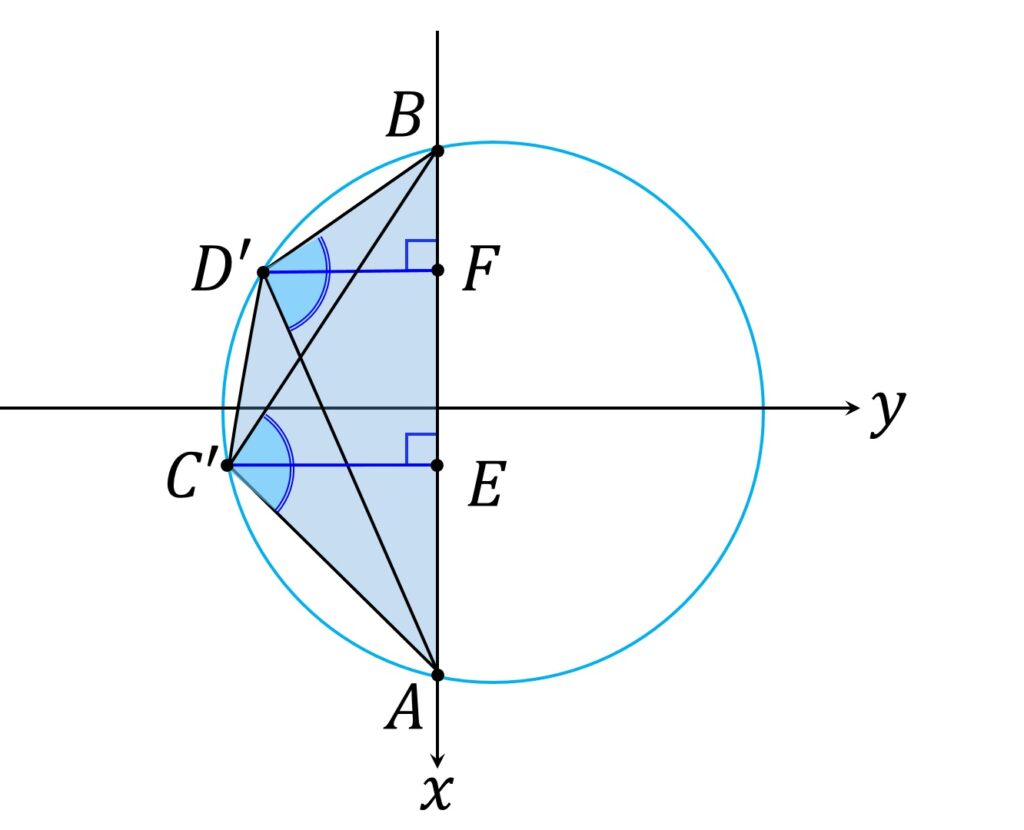
　要はC’,D’ が AB の片側に集まっているときに円に内接するポイントがある、ということで、直感的には確かにその通りだと思える結果です。

解法のポイント

　　まず図形を頭の中でぐるぐる動かして、問題の主旨をつかみましょう。本稿に示したように、 C’ や D’ がそれぞれ AB に垂直な平面上に常にあることに気が付けば、後の展開が楽になると思います。

　本問は対象とする図形が例えば正四面体のように定量的にカチッとしたものではないので、数式をきちっと立てて攻めるタイプの問題ではありません。このような場合は中間値の定理を利用して目標ポイントを絞り込みましょう。