1998年京大 後期 数学 第4問 は三角方程式の解で構成される数列の極限を求める問題です。問題文は以下のとおりです。
a は 0 < a < π を満たす定数とする.n = 0, 1, 2, · · · に対し,nπ < x < (n + 1)π の範囲に sin(x + a) = x sin x を満たす x がただ一つ存在するので,この x の値を xn とする.
(1) 極限値 \lim\limits_{n \to \infty} (x_n − n\pi) を求めよ.
(2) 極限値 \lim\limits_{n \to \infty} n(x_n − n \pi) を求めよ.
xn の一般項などとても求められそうにないので、知恵を絞る必要がありそうです。それでは見ていきましょう。
1998年京大 後期 数学 第4問 小問1の解法
まず Xn = xn – nπ と置きます。すると 0 < Xn < π であり、かつ
sin(Xn + nπ + a) = (Xn + nπ) sin(Xn + nπ )
なので
sin(Xn + a) = (Xn + nπ) sinXn
が成り立ちます。
fn(x) = (x + nπ) sinx は n が大きくなると x = 0 の近傍で傾きがどんどん大きくなる、つまりグラフが「立ち上がってくる」ので、y = f(x) = sin(x + a) と y = fn(x) の交点はどんどん0に近づく、すなわち \lim\limits_{n \to \infty} X_n = 0 が成り立つのではないかと予想できます(図1)。
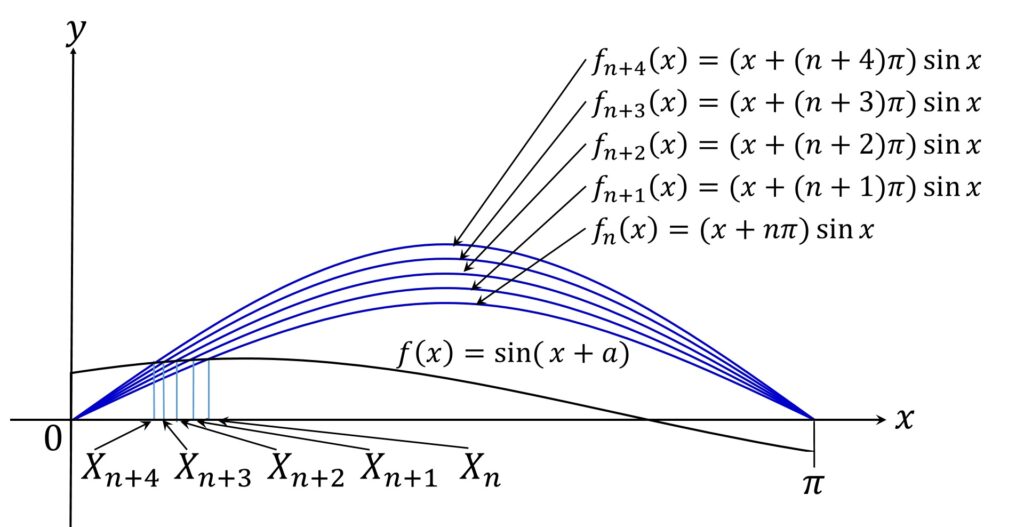
\lim\limits_{n \to \infty} X_n = 0 を証明するためには、0 < Xn なので Xn より大きくてしかも極限が0になる数列 Yn が見つかれば十分です。そこでそのような数列を探します。
ここで f(x) と fn(x) の大小関係を調べます。 f(x) = fn(x) は0 < x < π の範囲で解を1つしか持たず、しかも
f(0) = sina > 0 = fn(0)
f(π) = sin(π + a) = -sina < 0 = fn(π)
なので、 0 ≦ x < Xn の範囲で f(x) > fn(x) 、 Xn < x ≦ π の範囲で f(x) < fn(x) が成り立ちます(もしそうでなければ、中間値の定理により Xn とは異なる f(x) = fn(x) の解が存在することになってしまう)。
この性質を利用して Yn を探します。すなわち、 f(Yn) < fn(Yn) が成り立てば Xn < Yn なので、そのような Yn で0に収束するものを探します。
というわけでいささか安直ですが、
Y_n = \frac{1}nで試してみます。
まず明らかに
f(Yn) ≦ 1
が成り立ちます。
一方
\begin{aligned}
f_n(Y_n) & = (\frac{1}n + n \pi) \sin (\frac{1}n) \\
& > n \pi \sin (\frac{1}n) \\
\end{aligned}ですが、平均値の定理によりある実数 0 < c < \displaystyle\frac{1}n が存在して
n \sin (\frac{1}n) = \frac{\sin (\frac{1}n) }{\frac{1}n} = \cos c > \cos (\frac{1}n)が成り立ちます。したがって、 n ≧ 1 のとき
\frac{1}n \leqq 1 < \frac{\pi}3なので
n \sin (\frac{1}n) > \cos (\frac{1}n) > \frac{1}2が成り立ちます。
ゆえに n ≧ 1 のとき
f(Y_n) \leqq 1 < \frac{\pi}2 < f_n(Y_n)であり、0 < Xn < Yn が成り立つので
\lim_{n \to \infty} X_n = 0が成り立ちます。すなわち
\lim_{n \to \infty} (x_n − n\pi) = 0です。
1998年京大 後期 数学 第4問 小問2の解法
こいつは手強そうです。今度は0に収束するといった安直な答えでは無いはずなので、積分挟み撃ちなどを使って上からだけでなく下からも評価し、しかも上下の極限が一致するようにしなければなりません。
なんか無理ゲーじゃね、とも思いますが、ここで小問1の結果を利用して
sin(Xn + a) = (Xn + nπ) sinXn
の極限をとってみたら何かわかるかもしれません。
n\sin X_n = \frac{\sin (X_n +a) -X_n \sin X_n} {\pi}なので
\lim_{n \to \infty}n\sin X_n = \frac{\sin a} {\pi}です。
おおっ!
\lim_{x \to 0} \frac{ \sin x}{x} = 1なので Xn と sinXn の収束スピードは同程度であり、 したがって nXn は案外 nsinXn と同じ値に収束するかもしれません。
実際、
\begin{aligned}
\lim_{n \to \infty}nX_n & = \lim_{n \to \infty} (n \sin X_n \cdot \frac{X_n}{\sin X_n} )\\
& = \lim_{n \to \infty} \frac{n \sin X_n}{ \frac{\sin X_n}{X_n}} \\
& = \frac{ \lim\limits_{n \to \infty} n \sin X_n}{ \lim\limits_{n \to \infty} \frac{\sin X_n}{X_n}} \\
&= \frac{\sin a} {\pi}
\end{aligned}が成り立ちます。ゆえに
\lim_{n \to \infty}n(x_n − n \pi) = \frac{\sin a} {\pi}です。
解法のポイント
小問1はまず、 Xn が0に収束しそうだと当たりをつけることがポイントです。これが思いつければ、本稿で示したように0に収束する何かで上から押さえてみよう、という発想が自然に出てくると思います。
一方
sin(Xn + a) = (Xn + nπ) sinXn
なので
\begin{aligned}
|\sin X_n | & = \frac{ |\sin ( X_n + a) - X_n \sin X_n| }{n \pi} \\
&< \frac{1 + \pi}{ n \pi} \to 0 ( n \to \infty)
\end{aligned}であり、したがって
\lim_{n \to \infty} \sin X_n = 0が成り立ちます。ネット上ではここからいきなり \lim\limits_{n \to \infty} X_n = 0 を導き出しているケースもあります。直感的には明らかですが、逆関数の連続性は高校数学の範囲を超えるっぽいので、これに頼るのは入試では避けたほうが無難でしょう。
小問2は sin(Xn + a) = (Xn + nπ) sinXn の極限をとってみようと思いつければ、あとは容易に進められます。式の極限を取るというのはオーソドックスな攻め方なので、まずは試して見るようにしましょう。

