京大

　2023年京大 特色入試 数学 第1問 は平面図形の問題ですが、垂心というものを知っていれば、三角関数や微積分やその他の面倒な計算をせずに解くことが出来ます。問題文は以下のとおりです。

平面内の鋭角三角形 △AB

　2022年京大 数学 第6問 は漸化式の中に三角関数がある、なんかいやらしい問題です。問題文は以下のとおりです。

　数列 を次の式

\begin{aligned} & x_1=0 , x_{n+1}

　2023年京大 数学 第6問は、三角関数に素数を絡ませるという、危険な香りがたっぷりの問題です。問題文は以下のとおりです。

p を3以上の素数とする．また， を実数とする．
(1) と を の式として表せ ...

2023年京大 特色入試 数学 第4問 は、二項係数の剰余類に関する問題です。問題文は以下のとおりです。

p を3以上の素数とし， を整数とする．このとき， p2 以上の整数 n であって

　　　

　

2022年 京大 特色入試 第2問 は図形の面積に関する問題です。特色入試だからなのか、京大にしてはめずらしく、くどくどと長い問題文になっています。以下の通りです。

半径1の円 C の周上に相異なる5点 ...

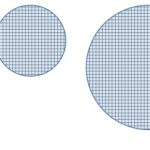
2004年 京大 後期 数学 第6問 は格子点と極限に関する問題です。問題分は以下のとおりです。

n を自然数とする。xy 平面内の原点を中心とする 半径 n の円の内部と周を合わせたものを Cn であらわす。次の条件を ...

2018年京大 数学 第2問 は、与えられた条件を満たす整数が素数であることを示せ、と言う問題です。問題文は以下の通りです。

が素数となるような整数 をすべて求めよ。

　京大はこの手の、ある式が素数になる条件 ...

2003年京大 後期 数学 第5問 は級数和の極限に関する問題です。問題文は以下の通りです。

以下の極限を求めよ：

　級数和の極限問題は、和を解析的に求められるケース（ など）の他は、積分挟み撃ちの

　2003年京大 数学 第4問 は多項式の割り算問題です。問題文は以下の通りです。

は で割り切れるか。

　京大の入試問題は相変わらず問題文が簡潔ですっきりしていて、好感度が高いです。これでさくっと解ければ言 ...

1999年京大 理系 後期 第4問 は空間図形の問題です。問題文は以下の通りです。

△ABC は鋭角三角形とする。このとき、各面すべてが △ABC と合同な四面体が存在することを示せ。

　京大の入試にはよく、「 ...