ブログアーカイブ
-
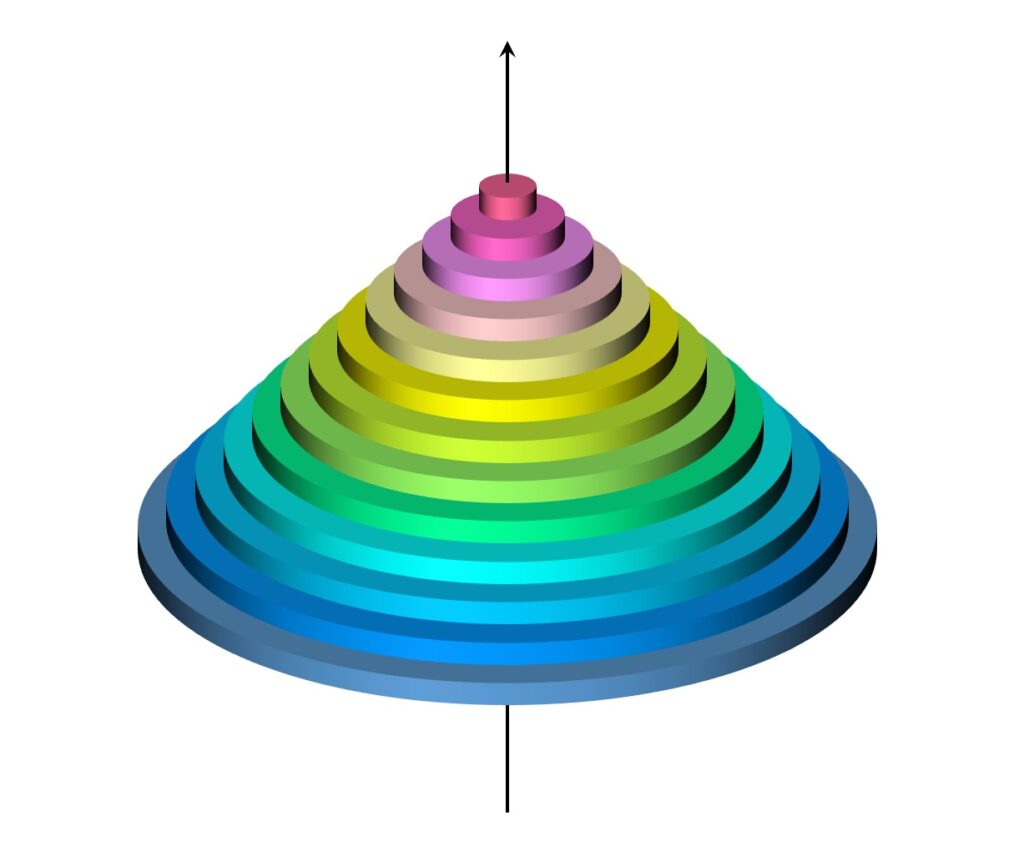
体積積分のブービートラップ – 2022年東大 数学 第5問
2022年東大 数学 第5問 は、図形が移動してできる軌跡の体積を求める問題です。問題分は以下のとおりです。 座標空間内の点 A(0,0,2) と点 B(1,0,1) を結ぶ線分 AB を z 軸のまわりに1回転させて得られる曲面を S とする。 S 上の点 P と xy 平面上の点 ... -

素数問題で再びアハ体験 – 2018年京大 数学 第2問
2018年京大 数学 第2問 は、与えられた条件を満たす整数が素数であることを示せ、と言う問題です。問題文は以下の通りです。 が素数となるような整数 をすべて求めよ。 京大はこの手の、ある式が素数になる条件を示せ的な問題が好きなようで、けっこう良... -

中学入試を考える
先日、朝日新聞に、中学入試に関する以下のような記事が載っていました。 算数、合否を分けた問題は 開成、渋渋、豊島岡 中学入試分析・後編 昔に比べて難しくなった、みたいな内容でしたが、その中で、渋谷学園渋谷中学の入試問題が引用されていました... -

大きく変わった出題傾向 – 2022年千葉県公立高校入試
2022年の千葉県公立高校入試の数学は、前年度から大きく傾向が変わりました。問題文と回答は、以下のリンク先をご覧ください。 産経ニュース 千葉県公立高校入試 問題と解答 ぱっと見の大きな変化は、大問の数が5から4に減っていることです。これま... -

伝説の超難問の解法まとめ – 1998年東大 数学 後期 第3問
史上最強の超難問として今なお君臨し続ける、1998年東大数学後期第3問。ネット上にはいろいろな解法がUPされており、本ブログでも過去に取り上げていますが、本稿ではそれらを紹介していきます。そして、各解法が本質的に2パターンに収斂することを示し... -

座標系で図形を回転させる鬼問題-2022年千葉県公立高 数学 第2問(3)
千葉県の公立高校入試問題の傾向が、2022年から大きく変わりました。定番であった規則性の問題が無くなっていたりしますが、本稿で取り上げる第2問は2次関数に図形を絡ませた問題で、これは以前の第3問に対応します。 基本的には、教科書レベルのさく... -

級数和の極限は東大でも積分挟み撃ち – 2001年東大 数学 後期 第3問
2001年東大 数学 後期 第3問 は、級数和の極限の問題です。問題文は以下の通りです。 整数を係数とする2次多項式 で2次の項が正のものが与えられている。任意の実数 に対して、平面上の原点を中心とし半径が1である単位円 C 上の点 を によって定める。... -

論理問題には背理法で挑め – 2001年東大 数学 第5問
2001年東大 数学 第5問 は、一見してどの分野の問題かわかりません。問題文も長く、捨て問オーラ全開です。問題文は以下の通りです。 容量 1 リットルの m 個のビーカー(ガラス容器)に水が入っている。m ≧ 4 で空のビーカーは無い。入っている水の総量... -

積分挟み撃ちで求める級数和の極限 – 2003年京大 後期 数学 第5問
2003年京大 後期 数学 第5問 は級数和の極限に関する問題です。問題文は以下の通りです。 以下の極限を求めよ: 級数和の極限問題は、和を解析的に求められるケース( など)の他は、積分挟み撃ちの手法を用いるケースが多く見られます。 特に本問は、... -
1の三乗根を応用した多項式の割り算 – 2003年京大 数学 第4問
2003年京大 数学 第4問 は多項式の割り算問題です。問題文は以下の通りです。 は で割り切れるか。 京大の入試問題は相変わらず問題文が簡潔ですっきりしていて、好感度が高いです。これでさくっと解ければ言うことありませんが、早速見ていきましょう...