峰企画の数学ブログ
白井市 印西市の家庭教師 は有限会社峰企画。数学の入試問題に関するブログを公開しています。問題の解法を分析するとともに、解法のポイントやそれにたどり着くための思考方法、更には類似問題対策のための学習方針を、幅広く考察していきます。
なお、各大学は入試問題の解答を公表していません。ブログ記事の解答、解法に関する記述は、各大学とは無関係のものです。
目次
新着記事
-
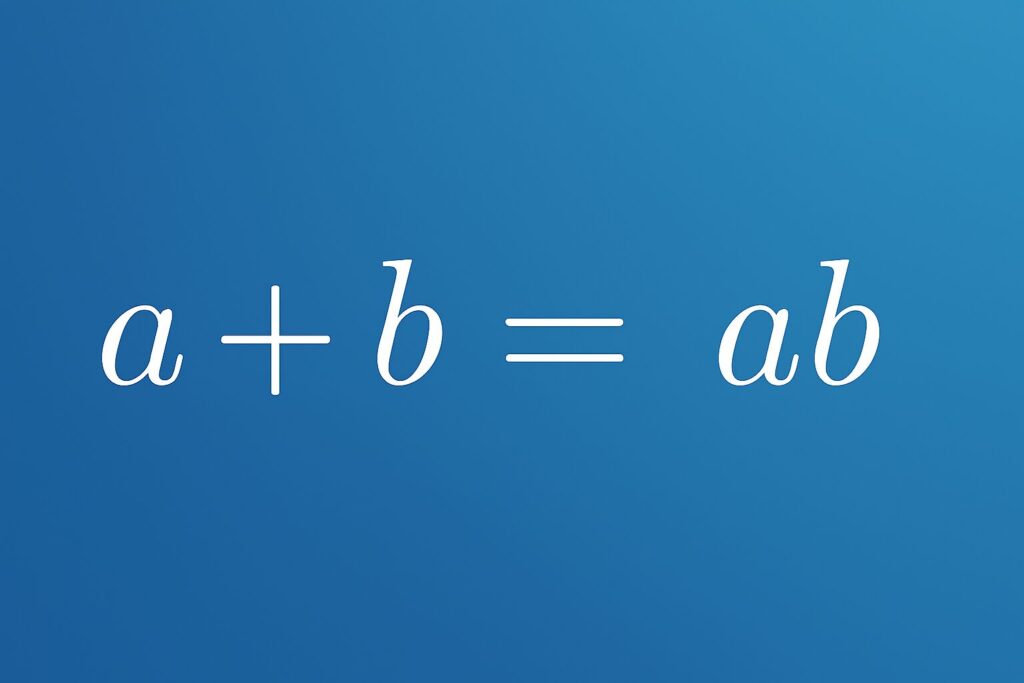
n 変数対称式の自然数解 – 1996年 東工大 数学 第1問
1996年 東工大 数学 第1問 はn 変数対称式の自然数解に関する問題です。問題文は以下の通りです。 2 以上の整数 n に対して方程式 の正の整数解 を考える.ただし,たとえば (1, 2, 3) と (3, 2, 1) は異なる解とみなす.このとき次の問に答えよ. (1) n… -

正三角形パネルの塗りつぶし問題 – 1997年東大 数学 後期 第1問
1997年東大 数学 後期 第1問 は正三角形パネルを順次塗りつぶしていったときに、塗りつぶされた数がどういう挙動をするかを回答する問題です。 問題文は以下のとおりで、東大2次試験からの引用です。 下の図のように,1 辺の長さが 1 の正三角形で,平… -

本質は3次の二面体群 – 1998年東大 数学 後期 第3問 小問2
「キングオブ難問」1998年東大 数学 後期 第3問の小問2にはいろいろな解法がありますが、主流はいわゆる交代和の剰余類を不変量関数に用いる手法です。 本稿では3次の二面体群を用いた証明を提示するとともに、小問2の主張が二面体群の性質に強く依存し…
人気順
-

空間分割の無理ゲー問題 – 2019年東工大 数学 第4問
今回取り上げる 2019年東工大 数学 第4問 は、解き方がちょっと見当もつきません。こりゃ無理ゲーってレベルじゃねえぞ的な超難問です。 問題文は結構長いので、引用は断念しました。ググると問題文を見つけることが出来ますので、そちらをご覧くださ… -

存在領域の難問 – 1988年東大 数学 第3問
1988年東大 数学 第3問 は、条件を満たす点の存在領域を求める問題です。問題文は以下の通りです。 を で与えられる 平面上の図形とする. 次の条件をみたす 平面上の点 全体の集合を図示せよ.条件:「 を平行移動した図形で, 点 を通り, かつもとの図形 と… -

ヒントを見逃したら二項係数の力ずく計算 – 2009年東大 数学 第1問
2009年東大 数学 第1問 は、二項係数に関する問題です。問題文は以下のとおりです。 自然数 m ≧ 2 に対し、 m-1 個の二項係数を考え、これらすべての最大公約数を dm とする。すなわち dm はこれらすべてを割り切る最大の自然数である。(1) mが素数なら…
学校別出題年別
東京大学
京都大学
東京工業大学
千葉県立高校
渋谷学園幕張高校
ラサール高校
全記事アーカイブ

峰企画の数学ブログ全記事は、こちらからご覧いただけます。
