2000年東大 数学 第4問 は余り見たことのない設問です。問題文は以下のとおりです。
座標平面上を運動する3点P,Q,Rがあり,時刻tにおける座標が次で与えられている.
\begin{aligned}
\mathrm{P} & :x= \cos t, y= \sin t \\
\mathrm{Q} & :x= 1−vt, y= \frac{\sqrt{3}}2 \\
\mathrm{R} &: x= 1−vt, y= 1
\end{aligned}ただし, v は正の定数である.この運動において,以下のそれぞれの場合に v のとりうる値の範囲を求めよ.
(1) 点 P と線分 QR が時刻 0 から 2π までの間ではぶつからない.
(2) 点 P と線分 QR がただ一度だけぶつかる.
題意を図示すると、以下のようになります。
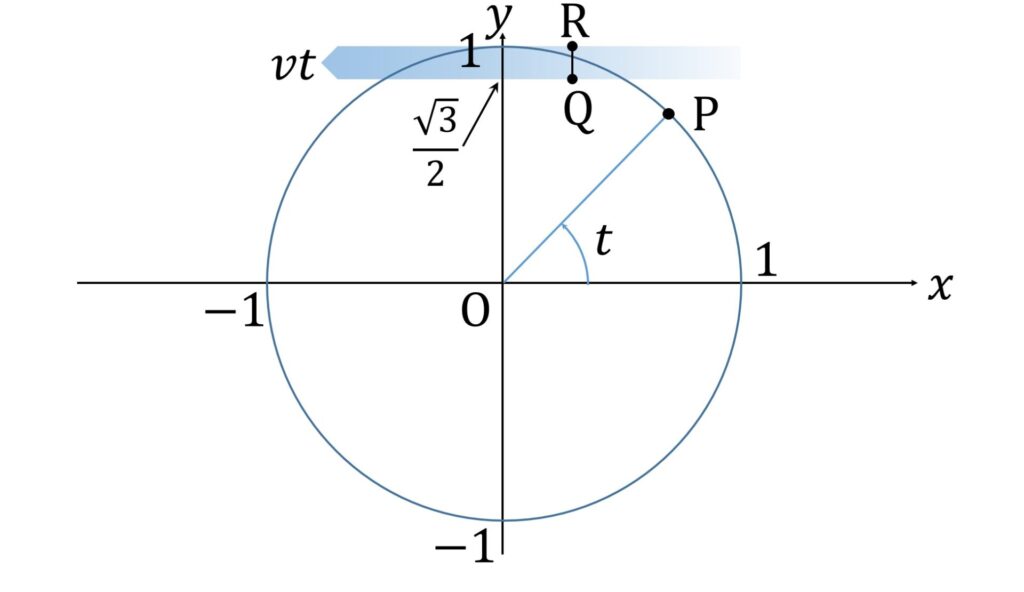
現実世界へのアナロジーとしては、大縄跳びを回転軸方向から見たところというのが最も近いと思います。点 P が大縄で、線分 QR がこれをくぐろうとする人です。
ありそうでなかった設問。こんな問題をよく思いつくものだと頭が下がりますが、頑張れば解けそうな気もします。それでは見ていきましょう。
2000年東大 数学 第4問 小問1の解法
小問1の内容は、大縄が1周するまでの間に引っかからずに通り抜けてください、というものです。人が縄に当たらない(点 P が線分 QR 上にない)状況より、縄にあたった状況(点 P が線分 QR 上にある)のほうが考えやすいので、まずはこれを定式化します。
P が QR 上にある必要十分条件
時刻 t において点 P が線分 QR 上にあるということは、その時刻において点 P が線分 QR の x 座標が等しいということです。したがって
1-vt= \cos t
が成り立ちます。
また、点 P が線分 QR 上にあるとき、点 P の y 座標は
\frac{\sqrt{3}}2 \leqq y \leqq 1を満たしますが、これが成り立つためには
\frac{\pi}3 \leqq t \leqq \frac{2\pi}3が成り立つことが必要です。
したがって、時刻 t において点 P が線分 QR 上にあるための必要条件は
1-vt= \cos t \\
\text{かつ} \\
\frac{\pi}3 \leqq t \leqq \frac{2\pi}3
が成り立つことです。
一方、これが十分条件であることは明らかです。よって、必要十分条件を求めることが出来ました。
P が QR 上にある必要十分条件をグラフで表現する
点 P と線分 QR の x 座標は時刻 t の関数です。そこで、
\begin{aligned}
f(t) & = 1-vt \\
g(t) &= \cos t
\end{aligned}と表記します。すると、点 P が線分 QR 上にあるための必要十分条件は、関数 x= f(t) と関数 x= g(t) のグラフが \displaystyle\frac{\pi}3 \leqq t \leqq \frac{2\pi}3 の範囲で交点を持つことです(図2)。
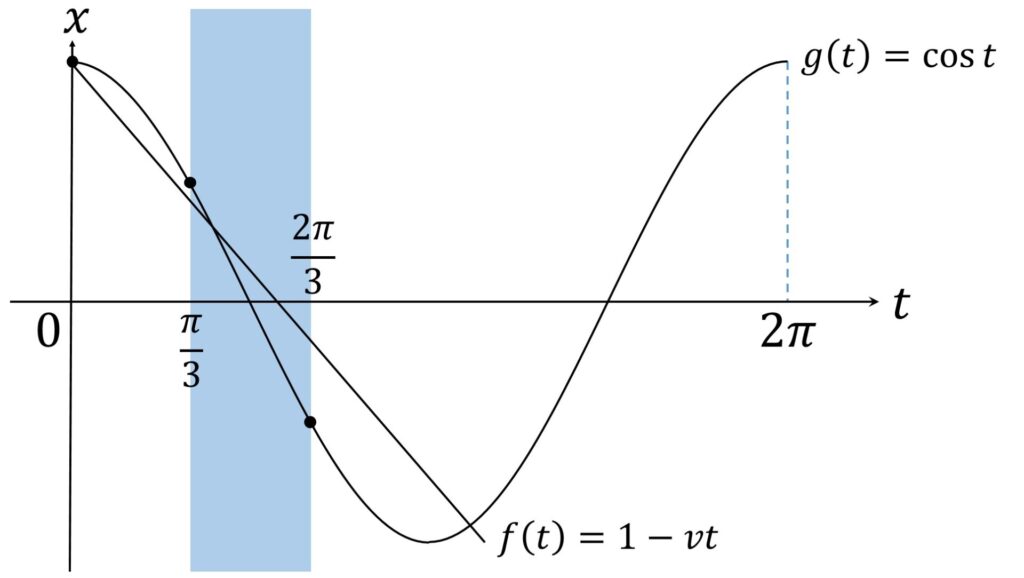
点 P と線分 QR が時刻 0 から 2π までの間ではぶつからないための必要十分条件
ここまでの考察より、点 P と線分 QR が時刻 0 から 2π までの間ではぶつからないための必要十分条件は、関数 x= f(t) と関数 x= g(t) のグラフが \displaystyle\frac{\pi}3 \leqq t \leqq \frac{2\pi}3 の範囲で交点を持たないことです。
これを満たす v の範囲は、グラフを書けば明らかです。 x= g(t) 上の3点 A,B,C を、
\begin{aligned}
\mathrm{A}(0,1),\mathrm{B}( \frac{\pi}3,\frac{1}2), \mathrm{C}( \frac{2\pi}3, - \frac{1}2)
\end{aligned}と置くとき、関数 x= f(t) と関数 x= g(t) のグラフが \displaystyle\frac{\pi}3 \leqq t \leqq \frac{2\pi}3 の範囲で交点を持たないための必要十分条件は、関数 x= f(t) のグラフがその範囲で直線 AB の上にあるか、または直線 AC の下にあることです(図3)。
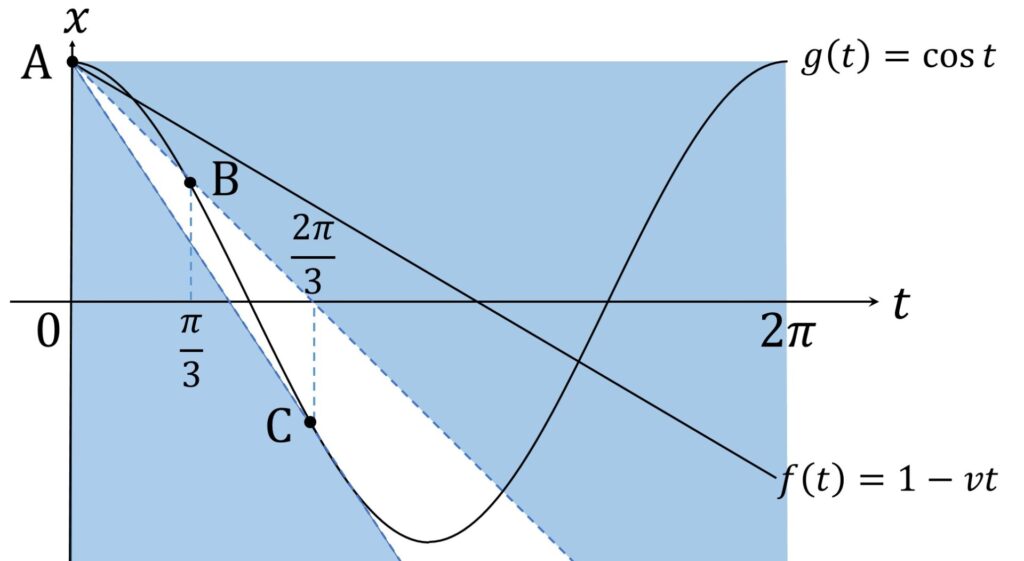
これを満たす v の範囲は、 AB の傾きが -\displaystyle\frac{3}{2 \pi} 、 AC の傾きが -\displaystyle\frac{9}{4 \pi} であることから、
0 < v < \frac{3}{2 \pi}, \frac{9}{4 \pi} < v \cdots(1)です。
v の範囲をもう少し厳密に求めてみる
上記のようなグラフを用いた定性評価でも全然問題ないはずですが、赤本など他の解法は増減表を書いたりしてもっとゴリゴリやっているので、念の為にもう少しきっちりした求め方を準備します。
まず、
\frac{3}{2 \pi} \leqq v \leqq \frac{9}{4 \pi} の場合を考えます。このとき、
f( \frac{ \pi}3) = 1 - \frac{ \pi}3 v \leqq \frac{1}2 = g( \frac{ \pi}3)f( \frac{ 2\pi}3) = 1 - \frac{ 2\pi}3 v \geqq - \frac{1}2 = g( \frac{ 2\pi}3)なので、中間値の定理によりある \displaystyle\frac{\pi}3 \leqq t_0 \leqq \frac{2\pi}3 が存在して
f(t_0) = g(t_0)
が成り立ちます。すなわち、 \displaystyle\frac{3}{2 \pi} \leqq v \leqq \frac{9}{4 \pi} ならば関数 x= f(t) と関数 x= g(t) のグラフが \displaystyle\frac{\pi}3 \leqq t \leqq \frac{2\pi}3 の範囲で交点を持つので、点 P と線分 QR が時刻 0 から 2π までの間でぶつかります。
この対偶を取ることで、条件(1)は点 P と線分 QR が時刻 0 から 2π までの間ではぶつからないための必要条件であることがわかりました。
次に十分性の証明です。正の実数 v が与えられたとき、 t の関数 hv(t) を
\begin{aligned}
h_v(t) & = g(t) -f(t) \\
& = \cos t +vt -1
\end{aligned}と定義します。
まず 0 < v < \displaystyle\frac{3}{2 \pi} の場合です。このとき \displaystyle\frac{\pi}3 \leqq t \leqq \frac{2\pi}3 の範囲で
\begin{aligned}
\frac{d}{dt} h_v(t) = & - \sin t+v \\
\leqq & - \frac{\sqrt{3}}2+ v \\
= & - \frac{\sqrt{3}}2 +\frac{3}{2 \pi} \\
< & - \frac{\sqrt{3}}2 +\frac{1}{2 } < 0
\end{aligned}であり、 hv(t) は単調減少です。
ところが
\begin{aligned}
h_v( \frac{\pi}3) = & \cos \frac{\pi}3 +\frac{\pi}3 v -1 \\
= & - \frac{1}2+\frac{\pi}3 v \\
< & - \frac{1}2+ \frac{\pi}3 \cdot \frac{3}{2 \pi} =0
\end{aligned}なので、 \displaystyle\frac{\pi}3 \leqq t \leqq \frac{2\pi}3 の範囲で hv(t) < 0 です。すなわちその範囲で関数 x= f(t) と関数 x= g(t) のグラフは交点を持たず、点 P と線分 QR が時刻 0 から 2π までの間ではぶつかりません。
一方、 v_0 = \displaystyle\frac{9}{4 \pi} と置くとき、 \displaystyle\frac{\pi}3 \leqq t \leqq \frac{2\pi}3 の範囲で
\begin{aligned}
\frac{d}{dt} h_{v_0}(t) = & - \sin t+v_0 \\
\leqq & - \frac{\sqrt{3}}2+ v_0 \\
= & - \frac{\sqrt{3}}2 +\frac{9}{4 \pi} \\
< & - \frac{\sqrt{3}}2 +\frac{3}{4 } < 0
\end{aligned}です。
\begin{aligned}
h_{v_0}(\frac{2 \pi}3) & = \cos \frac{2 \pi}3 +v_0 \frac{2 \pi}3 -1 \\
& = -\frac{1}2+ \frac{2 \pi}3 \cdot \frac{9}{4 \pi} -1 =0
\end{aligned}なので \displaystyle\frac{\pi}3 \leqq t \leqq \frac{2\pi}3 の範囲で
h_{v_0}(t) = \cos t + v_0 t -1 \geqq 0です。
ところが \displaystyle\frac{9}{4 \pi} < v のとき、明らかに
h_{v_0}(t) < h_v (t)なので、 \displaystyle\frac{\pi}3 \leqq t \leqq \frac{2\pi}3 の範囲で
0 < h_v (t)
すなわちその範囲で
f(t) < g(t)
が成り立ち、関数 x= f(t) と関数 x= g(t) のグラフは交点を持たないので、点 P と線分 QR が時刻 0 から 2π までの間ではぶつかりません。
時間の限られた入試問題であることを考えると、本当にここまで必要なのかいささか疑問では有りますが、参考にしてみてください。
2000年東大 数学 第4問 小問2の解法
小問2は、縄に1回だけあたってから抜けてください、という内容です。縄の回転数に制限はありません。当たるのが1回であれば、何回目であたってもOKですが、当たる回数が1回だけ、というのがミソです。グズグズしていると2度3度と縄にあたってしまうので、移動速度 v の調整が難しくなってきます。
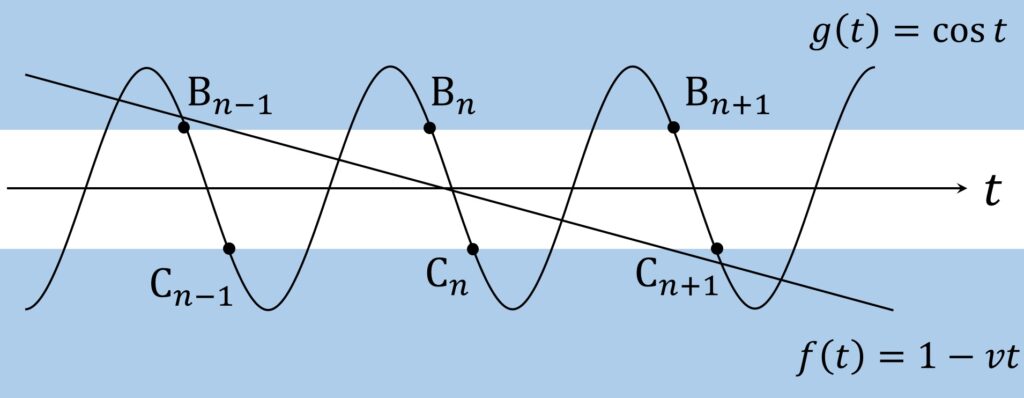
点 P と線分 QR が1回だけ当たるための必要十分条件
縄すなわち点 P の回転サイクルを、非負整数 n で表すことにします。1サイクル目を n=0 、2サイクル目を n=1 というように振っていきます。
この n に対し、時刻 tn 、 sn を
\begin{aligned}
t_n = & 2n\pi+ \frac{\pi}3 \\
s_n = & 2n\pi+ \frac{2\pi}3 \\
\end{aligned}と定義します。また、グラフ x = g(t) 上の点 Bn,Cn を以下のように定義します。
\begin{aligned}
\mathrm{B}_n(t_n,g(t_n)), \mathrm{C}_n( s_n,g(s_n))
\end{aligned}このとき、n サイクル目で1回だけ当たるための必要十分条件は明らかに、
\begin{aligned}
&x=f(t) \text{のグラフが} \mathrm{B}_{n-1} \text{の上を通り} \\
\text{かつ} & x=f(t) \text{のグラフが} \mathrm{B}_{n} \text{の下を通り} \\
\text{かつ} & x=f(t) \text{のグラフが} \mathrm{C}_{n} \text{の上を通り} \\
\text{かつ} & x=f(t) \text{のグラフが} \mathrm{C}_{n+1} \text{の下を通る} \\
\end{aligned}です(図4)。
これを式で表すと、以下のとおりです。
f(t_{n-1}) > g(t_{n-1}) \\
\text{かつ} \\
f(t_n) \leqq g(t_n) \\
\text{かつ} \\
f(s_n) \geqq g(s_n) \\
\text{かつ} \\
f(s_{n+1}) < g(s_{n+1}) \\
ただし、 n=0 のときだけは1つ目の不等式はありません。
なお、ぶつかる回数が1回なのは、 f(t) の傾き -v が tn ≦ t ≦ sn の範囲でg(t) の微分より常に大きいことから明らかです。
これを v が満たすべき条件に書き換えると、以下のとおりです。
\begin{aligned}
1- \{ 2(n-1) \pi + \frac{\pi}3 \}v & > \frac{1}2 \\
\text{かつ} \\
1- (2n \pi + \frac{\pi}3 ) v & \leqq \frac{1}2 \\
\text{かつ} \\
1- (2n \pi + \frac{2 \pi}3 )v & \geqq - \frac{1}2 \\
\text{かつ} \\
1- \{2(n+1) \pi + \frac{2 \pi}3 \}v& < - \frac{1}2 \\
\end{aligned}さらに、 v について整理すると
\begin{aligned}
&v < \frac{3}{(12n -10 )\pi} \\
\text{かつ} \\
\frac{3}{(12n +2 )\pi} \leqq & v \\
\text{かつ} \\
& v \leqq \frac{9}{(12n +4 )\pi} \\
\text{かつ} \\
\frac{9}{(12n +16 )\pi} < & v \\
\end{aligned}です。
v の範囲を求める
同じ向きの不等号が2つずつあるので、まず不等式の左側の
\frac{3}{(12n +2 )\pi} ,\frac{9}{(12n +16 )\pi} について、どちらが大きいかを判定します。
\begin{aligned}
& \frac{9}{(12n +16 )\pi} -\frac{3}{(12n +2 )\pi} \\
= & \frac{9(12n +2 ) - 3(12n +16 )}{(12n +16 )(12n +2 )\pi} \\
= & \frac{6(12n -5 ) }{(12n +14 )(12n +2 )\pi} \\
\end{aligned}なので、 n=0 のとき
\frac{3}{2 \pi} > \frac{9}{16 \pi} n ≧ 1 のとき
\frac{3}{(12n +2 )\pi} <\frac{9}{(12n +16 )\pi} です。
次に不等式の右側の
\frac{3}{(12n -10 )\pi} ,\frac{9}{(12n +4 )\pi} について、どちらが小さいかを判定します。
n=0 のときは
\frac{9}{(12 \times 0 +4 )\pi} = \frac{9}{4 \pi}の不戦勝です。
n ≧ 1 のとき、
\begin{aligned}
& \frac{9}{(12n +4 )\pi} -\frac{3}{(12n -10 )\pi} \\
= & \frac{9(12n -10 ) - 3(12n +4 ) }{(12n +4 )(12n -10 )\pi} \\
= & \frac{6(12n- 17) }{(12n +4 )(12n -10 )\pi} \\
\end{aligned}なので、 n=1 のとき
\frac{3}{2\pi} >\frac{9}{16\pi} n ≧ 2 のとき
\frac{3}{(12n -10 )\pi} <\frac{9}{(12n +4 )\pi} です。
したがって v の範囲は n=0 のとき
\frac{3}{2 \pi } \leqq v \leqq \frac{9}{4 \pi}n=1 のとき
\frac{9}{28 \pi } < v \leqq \frac{9}{16 \pi}n ≧ 2 のとき
\frac{9}{(12n +16) \pi } < v < \frac{3}{(12n-10)\pi}です。
なんかいい感じに結果が出てきましたが、ここで注意しなければならないのは、 n が大きくなるにつれて v が0に近づくことです。 v というのは線分 QR の移動速度であって、これがあまりに小さくなると、点 P が1周する間に QR が円周を通り抜けることができなくなります。
そこで
\frac{9}{(12n +16) \pi } , \frac{3}{(12n-10)\pi}の大小を調べます。
\begin{aligned}
&\frac{3}{(12n-10)\pi} - \frac{9}{(12n +16) \pi } \\
= & \frac{3(12n +16) - 9(12n-10)}{(12n-10)(12n +16) \pi} \\
=& \frac{6(-12n + 23)}{(12n-10)(12n +16) \pi} \\
\end{aligned}なので、 n ≧ 2 のとき常に
\frac{9}{(12n +16) \pi } > \frac{3}{(12n-10)\pi}です。
したがって n ≧ 2 のときの不等式
\frac{9}{(12n +16) \pi } < v < \frac{3}{(12n-10)\pi}は常に成り立ちません。ゆえに求める v の範囲は
\frac{9}{28 \pi } < v \leqq \frac{9}{16 \pi},\frac{3}{2 \pi } \leqq v \leqq \frac{9}{4 \pi}です。
小問2の必要十分条件を厳密に求める
小問1と同じように、必要十分条件を厳密に求めてみます。
点 P の回転サイクル n ≧ 0 に対し、時刻 tn 、 sn を
\begin{aligned}
t_n = & 2n\pi+ \frac{\pi}3 \\
s_n = & 2n\pi+ \frac{2\pi}3 \\
\end{aligned}と定義します。また、グラフ x = g(t) 上の点 Bn,Cn を以下のように定義します。
\begin{aligned}
\mathrm{B}_n(t_n,g(t_n)), \mathrm{C}_n( s_n,g(s_n))
\end{aligned}n サイクル目で点 P が線分 QR に1回だけぶつかる必要十分条件
このとき、 n サイクル目で点 P が線分 QR にぶつかる必要十分条件は、小問1で求めたのと同じ手法によって
\begin{aligned}
\frac{3}{(12n +2 )\pi} \leqq v \leqq \frac{9}{(12n +4 )\pi} \\
\end{aligned}であることがわかります。
ぶつかる回数が1回なのはうえで示したとおり、 tn ≦ t ≦ sn の範囲で
\frac{ \sqrt{3}}2 \leqq g(t)= \sin t \leqq 1であり、かつ、すべての n ≧ 0 に対して
\begin{aligned}
v \leqq \frac{9}{(12n +4 )\pi} < \frac{\sqrt{3}}2\\
\end{aligned}なので、tn ≦ t ≦ sn の範囲で関数
\begin{aligned}
h_v(t) & = g(t) -f(t) \\
& = \cos t +vt -1
\end{aligned}の導関数が負であることと、
\begin{aligned}
h_v(t_n)= & g(t_n)-f(t_n) \\
= & \frac{1}2+(2n\pi+ \frac{\pi}3) v -1 \\
\geqq & -\frac{1}2+(2n\pi+ \frac{\pi}3) \cdot \frac{3}{(12n +2 )\pi} \\
= & -\frac{1}2 +\frac{1}2 =0
\end{aligned}\begin{aligned}
h_v(s_n)= & g(s_n)-f(s_n) \\
= &- \frac{1}2+(2n\pi+ \frac{2\pi}3) v -1 \\
\leqq & -\frac{3}2+(2n\pi+ \frac{2\pi}3) \cdot \frac{9}{(12n +4 )\pi} \\
= & -\frac{3}2 +\frac{3}2 =0
\end{aligned}であることから明らかです。
ところが、
\begin{aligned}
\frac{3}{(12n +2 )\pi} \leqq v \leqq \frac{9}{(12n +4 )\pi} \\
\end{aligned}は
f(t_n) \leqq g(t_n) \\
\text{かつ} \\
f(s_n) \geqq g(s_n) \\
と同値です。
n サイクル目で点 P が線分 QR に1回だけぶつかり、かつ n-1 サイクル以下で点 P が線分 QR にぶつからない必要十分条件
n-1 サイクル目で点 P が線分 QR にぶつかる必要十分条件は
f(t_{n-1}) \leqq g(t_{n-1}) \\
\text{かつ} \\
f(s_{n-1}) \geqq g(s_{n-1}) \\
なので、n-1 サイクル目で点 P が線分 QR にぶつからない必要十分条件は
f(t_{n-1}) > g(t_{n-1}) \\
\text{または} \\
f(s_{n-1}) < g(s_{n-1}) \\
です。
したがってn サイクル目で点 P が線分 QR に1回だけぶつかり、かつ n-1 サイクル目で点 P が線分 QR にぶつからない必要十分条件は
f(t_n) \leqq g(t_n) \\
\text{かつ} \\
f(s_n) \geqq g(s_n) \\
\text{かつ} \\
\left (\begin{aligned}f(t_{n-1}) > g(t_{n-1}) \\
\text{または } \\
f(s_{n-1}) < g(s_{n-1}) \end{aligned} \right)\\となりますが、 f(s_n) \geqq g(s_n) であることと f(t) が単調減少関数であることから
f(s_{n-1}) \geqq f(s_n) \geqq g(s_n) =- \frac{1}2 = g(s_{n-1})であり、n サイクル目で点 P が線分 QR に1回だけぶつかるなら f(s_{n-1}) < g(s_{n-1}) は成り立ちません。
よってn サイクル目で点 P が線分 QR に1回だけぶつかり、かつ n-1 サイクル目で点 P が線分 QR にぶつからない必要条件は
f(t_n) \leqq g(t_n) \\
\text{かつ} \\
f(s_n) \geqq g(s_n) \\
\text{かつ} \\
f(t_{n-1}) > g(t_{n-1}) \\
です。
f(t_{n-1}) > g(t_{n-1}) ならば、 m ≦ n-1 であるすべての非負整数 m に対し
f(t_{m}) \geqq f(t_{n-1}) > g(t_{n-1}) = \frac{1}2 = g(t_{m})であり、 n-1 サイクル以下で点 P が線分 QR にぶつかることはありません。ゆえに、n サイクル目で点 P が線分 QR に1回だけぶつかり、かつ n-1 サイクル以下で点 P が線分 QR にぶつからない必要条件は
f(t_n) \leqq g(t_n) \\
\text{かつ} \\
f(s_n) \geqq g(s_n) \\
\text{かつ} \\
f(t_{n-1}) > g(t_{n-1}) \\
です。また、これの十分性は明らかです。
n サイクル目で点 P が線分 QR に1回だけぶつかり、かつ n+1 サイクル以上で点 P が線分 QR にぶつからない必要十分条件
上記と同じ論理展開により、
f(t_n) \leqq g(t_n) \\
\text{かつ} \\
f(s_n) \geqq g(s_n) \\
\text{かつ} \\
f(s_{n+1}) < g(s_{n+1}) \\
であることがわかります。
以上、小問2の必要十分条件は
f(t_{n-1}) > g(t_{n-1}) \\
\text{かつ} \\
f(t_n) \leqq g(t_n) \\
\text{かつ} \\
f(s_n) \geqq g(s_n) \\
\text{かつ} \\
f(s_{n+1}) < g(s_{n+1}) \\
であることが示せました。
解法のポイント
何と言っても、線分や点の位置をグラフで表現しようと思いつくことが第一です。それも、直線やサインカーブと言った初等的なグラフで表現することがポイントです。これにより証明の方針が立てやすくなる他、交点の有無や個数を難しい計算をせずに「明らかである」で押し通しやすくなります。交点がどうとか言う問題に遭遇したら、グラフを書いてイメージをつかむようにしましょう。
