1994年東大 数学 第6問 はL1ノルムに関する問題です。L1ノルムはマンハッタン距離と呼ばれることもありますが、L1ノルムといえば絶対値。これを開くための場合分けに脳が沸騰します。問題文は以下のとおりで、東大第2次試験問題からの引用です。
xy 平面上の 2 点 P, Q に対し,P と Q を x 軸または y 軸に平行な線分からなる折れ線で結ぶときの経路の長さの最小値を d(P, Q) で表す。
(1) 原点 O(0, 0) と点 A(1, 1) に対し,d(O, P) = d(P, A) をみたす点 P(x, y) の範囲を xy 平面上に図示せよ。
(2) 実数 a ≧ 0 に対し,点 Q(a, a2 + 1) を考える。次の条件 (∗) を満足する点 P(x, y) の範囲を xy 平面上に図示せよ。
(∗) 原点 O(0, 0) に対し,d(O, P) = d(P, Q) となるような a ≧ 0 が存在する。
本問における d(P, Q) は、ベクトル \overrightarrow{\mathrm{PQ}} の各成分の絶対値の和です。この量のことをL1ノルムと呼びます。設問についてのとっかかりの印象は大したことなさそうにも思えますが、実は最凶ラスボス級難問です。それでは見ていきましょう。なお、本稿の内容は東大が発表したものではありません。
1994年東大 数学 第6問 小問1の解法
d(O, P) 、 d(P, A) は以下のように書き下させます。
\begin{aligned}
d( \mathrm{O}, \mathrm{P} ) & = |x| +|y| \\
d( \mathrm{P} ,\mathrm{A}) &= |x-1| +|y-1| \\
\end{aligned}これらの絶対値を外すためには、 x,y の双方とも以下のように3つの範囲に分類する必要があります。
\begin{aligned}
&x < 0 \\
&0 \leqq x < 1 \\
& 1 \leqq x \\
& y < 0 \\
& 0 \leqq y < 1 \\
& 1 \leqq y \\
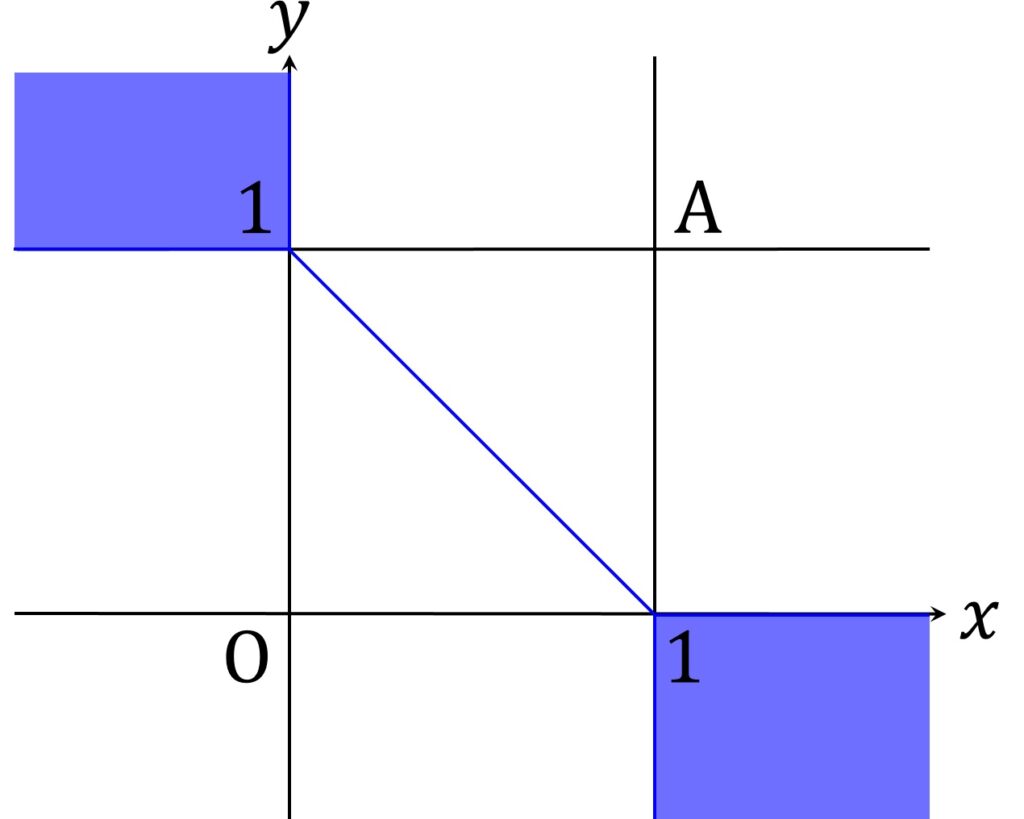
\end{aligned}よって場合分けの総数は 3 ☓ 3 = 9 通りですが、 x, y の対称性に着目して x ≧ y の範囲だけを考慮して5パターン分を考え、あとで直線 y = x に関して対称になるように貼り付ければ、手間が約半分になります(図1)。
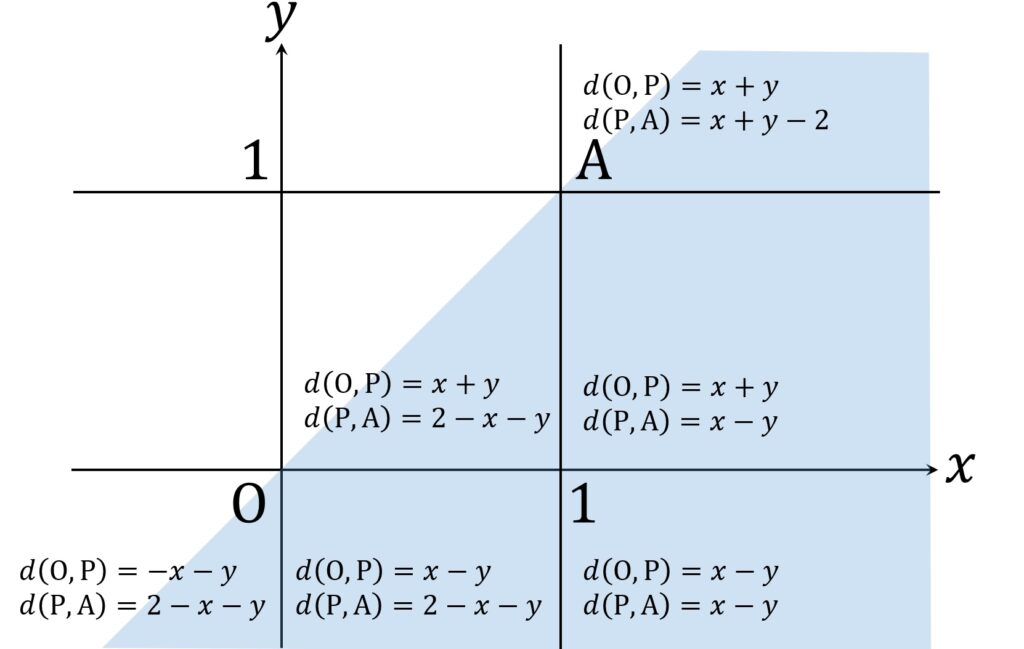
各パターンごとに、d(O, P) = d(P, A) を満たす P がどのように分布しているかを調べます。
x < 0 かつ y < 0 のとき
\begin{aligned}
d( \mathrm{O}, \mathrm{P} ) & = -x-y \\
d( \mathrm{P} ,\mathrm{A}) &= 2-x-y \\
\end{aligned}なので d(O, P) = d(P, A) を満たす P は存在しません。
0 ≦ x < 1 かつ y < 0 のとき
\begin{aligned}
d( \mathrm{O}, \mathrm{P} ) & = x-y \\
d( \mathrm{P} ,\mathrm{A}) &= 2-x-y \\
\end{aligned}なので d(O, P) = d(P, A) を満たす P は x = 1 上に存在しますが、これはエリア外です。
1 ≦ x かつ y < 0 のとき
\begin{aligned}
d( \mathrm{O}, \mathrm{P} ) & = x-y \\
d( \mathrm{P} ,\mathrm{A}) &= x-y \\
\end{aligned}なので d(O, P) = d(P, A) は恒等式になり、 P はエリア内のどこにあってもOKです。
0 ≦ x < 1 かつ 0 ≦ y < 1 のとき
\begin{aligned}
d( \mathrm{O}, \mathrm{P} ) & = x+y \\
d( \mathrm{P} ,\mathrm{A}) &= 2-x-y \\
\end{aligned}なので d(O, P) = d(P, A) を満たす P は直線 x + y = 1 上に存在します。
1 ≦ x かつ 0 ≦ y < 1 のとき
\begin{aligned}
d( \mathrm{O}, \mathrm{P} ) & = x+y \\
d( \mathrm{P} ,\mathrm{A}) &= x-y \\
\end{aligned}なので d(O, P) = d(P, A) を満たす P は直線 y = 0 上に存在します。
1 ≦ x かつ 1 ≦ y のとき
\begin{aligned}
d( \mathrm{O}, \mathrm{P} ) & = x+y \\
d( \mathrm{P} ,\mathrm{A}) &= x+y -2 \\
\end{aligned}なので d(O, P) = d(P, A) を満たす P は存在しません。
以上をまとめると、 d(O, P) = d(P, A) を満たす P は図2に示すエリアに存在します。
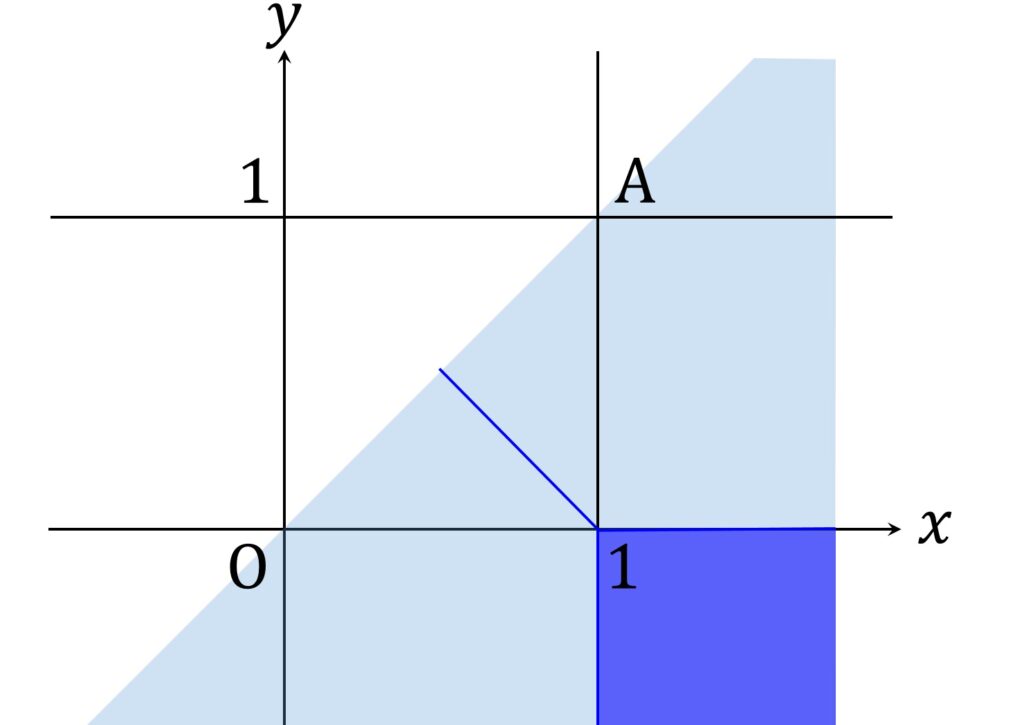
ゆえに P が存在する範囲は図3の通りです(境界含む)。