1998年東大 数学 前期 第3問は、平面図形と数列の問題です。これは解法の先取りというか、ネタバレですが、解いていくうちにフィボナッチ数列が、思いがけず現れてきます。
問題文は以下の通りです。
xy 平面に2つの円
C_0 : x^2 + ( y- \frac{1}{2} )^2 = \frac{1}{4}
C_1 : (x-1)^2 + ( y- \frac{1}{2} )^2 = \frac{1}{4}
をとり、 C_2 を x 軸と C_0 、 C_1 に接する円とする。さらに、 n= 2,3, \cdots に対して C_{n+1} を x 軸と C_{n} 、 C_{n-1} に接する円で C_{n-2} とは異なるものとする。 C_n の半径を r_n 、 C_n と x 軸との接点を (x_n, 0 ) として
q_n = \frac{1}{ \sqrt{2r_n} }
p_n = q_n x_n
とおく。
(1) q_n は整数であることを示せ。
(2) p_n も整数で、 p_n と q_n は互いに素であることを示せ。
(3) \alpha を \alpha = \frac{1}{1+ \alpha} を満たす正の数として、不等式
| x_{n+1} - \alpha | < \frac{2}{3} |x_{n} - \alpha |
を示し、極限 \lim_{n \to \infty} x_n を求めよ。
平方根の逆数が整数になることを示せ、とか、なかなか厳しそうです。何か、ドロドロになりそうな予感がします。
小問1の解法
ある数が整数であることを示すには、どうアプローチすればよいのでしょうか。見当もつきませんが、まずは漸化式を立てることを目指します。具体的な式の形を見れば、何か知恵が湧いてくるかも知れません。
図を描く
図形の問題なので、図を書いてみます。まず、初期値です(図1)。
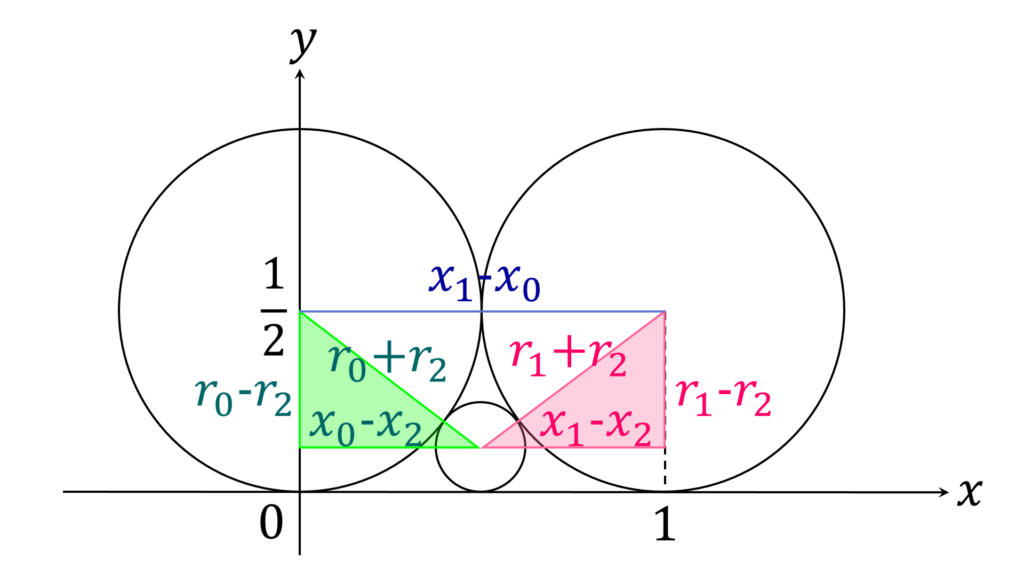
ちょっとした計算で、 x_2 = \frac{1}{2} ,r_2 = \frac{1}{8} , q_2 = 2 であることがわかります。最初の3項 n=0,1,2 の値を表にまとめると、以下の通りです。
| n | x_n | r_n | q_n |
|---|---|---|---|
| 0 | 0 | \frac{1}{2} | 1 |
| 1 | 1 | \frac{1}{2} | 1 |
| 2 | \frac{1}{2} | \frac{1}{8} | 2 |
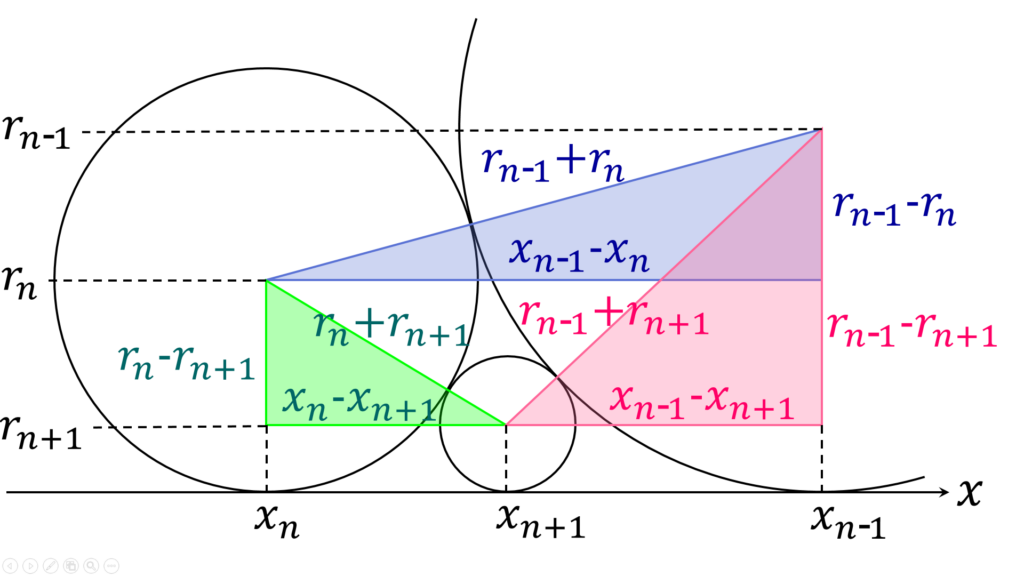
次に、一般項です(図2)。
式を立てる
各円 C_n の中心座標は (x_n, r_n) 、半径は r_n です。これと、各円 C_{n-1} , C_n , C_{n+1} がたがいに接しているという条件から、3平方の定理を適用して以下の3つの式を立てられます (n \geqq 2 ) 。
\begin{aligned}
& (x_{n-1} - x_{n} )^2 + (r_{n-1} - r_{n} )^2 \\
& = (r_{n-1} + r_{n} )^2 \\
\\
&(x_{n} - x_{n+1} )^2 + (r_{n} - r_{n+1} )^2 \\
& = (r_{n} + r_{n+1} )^2 \\
\\
& (x_{n-1} - x_{n+1} )^2 + (r_{n-1} - r_{n+1} )^2 \\
&= (r_{n-1} + r_{n+1} )^2
\end{aligned}r_n の項を右辺に移項して、
\begin{aligned}
& (x_{n-1} - x_{n} )^2 = 4r_{n-1} r_{n} \\
&(x_{n} - x_{n+1} )^2 = 4r_{n} r_{n+1} \\
& (x_{n-1} - x_{n+1} )^2 = 4r_{n-1} r_{n+1} \\
\end{aligned}ここで r_n を q_n に置き換えると、
\begin{aligned}
& (x_{n-1} - x_{n} )^2 = \frac{1}{q_{n-1}^2 q_{n} ^2 } \\
&(x_{n} - x_{n+1} )^2 = \frac{1}{q_{n}^2 q_{n+1} ^2 } \\
& (x_{n-1} - x_{n+1} )^2 = \frac{1}{q_{n-1}^2 q_{n+1} ^2 } \\
\end{aligned}両辺ともいい感じに2乗項だけになりました。 q_n を r_n の平方根で定義していたのは、このためだったのか。
次に、両辺を \frac{1} {2} 乗します。
\begin{aligned}
& |x_{n-1} - x_{n} | = \frac{1}{q_{n-1} q_{n} } \\
& |x_{n} - x_{n+1} | = \frac{1}{q_{n} q_{n+1} } \\
& | x_{n-1} - x_{n+1} | = \frac{1}{q_{n-1} q_{n+1} } \\
\end{aligned}絶対値記号を外す
左辺の絶対値記号を外したいので、各 x_n の大小関係を確認します。
各円 C_{n-1} , C_n , C_{n+1} がたがいに接しているという条件から、
x_{n} < x_{n+1} < x_{n-1}か、
x_{n-1} < x_{n+1} < x_{n}のいずれかなので、
\begin{aligned}
& x_{n-1} - x_{n} > 0 \\
& x_{n} - x_{n+1} <0 \\
& x_{n-1} - x_{n+1} > 0 \\
\end{aligned}か
\begin{aligned}
& x_{n-1} - x_{n} < 0 \\
& x_{n} - x_{n+1} >0 \\
& x_{n-1} - x_{n+1} < 0 \\
\end{aligned}のいずれかです。したがって、以下の式が成り立ちます(複号同順)。
\begin{aligned}
& x_{n-1} - x_{n} = \pm \frac{1}{q_{n-1} q_{n} } \\
& x_{n} - x_{n+1} = \mp \frac{1}{q_{n} q_{n+1} } \\
& x_{n-1} - x_{n+1} = \pm \frac{1}{q_{n-1} q_{n+1} } \\
\end{aligned}q_n の漸化式を求める
ここで、3つ目の式の両辺に -1 をかけて、符号を入れ替えます。
\begin{aligned}
& x_{n-1} - x_{n} = \pm \frac{1}{q_{n-1} q_{n} } \\
& x_{n} - x_{n+1} = \mp \frac{1}{q_{n} q_{n+1} } \\
& -x_{n-1} + x_{n+1} = \mp \frac{1}{q_{n-1} q_{n+1} } \\
\end{aligned}複号は同順です。辺々足すと、左辺はいい感じに0になるので、以下の式を得ます。
\begin{aligned}
& \frac{1}{q_{n-1} q_{n} } - \frac{1}{q_{n} q_{n+1} } - \frac{1}{q_{n-1} q_{n+1} } = 0\\
\end{aligned}分母を払うと、
\begin{aligned}
& q_{n+1} - q_{n-1} - q_{n} = 0\\
\end{aligned}すなわち
\begin{aligned}
& q_{n+1} = q_{n} + q_{n-1} \text{ } \cdots (1)\\
\end{aligned}で、これはまさにフィボナッチ数列です (n \geqq 2 ) 。
q_1 = 1 、 q_2 = 2 なので、以下、逐次的に q_n が整数であることが示せます。
なお、 q_0 = 1 であることから、式(1) は n \geqq 1 の範囲で成り立ちます。
小問2の解法
式を立てる
まず、 p_n の式を立ててみます。
小問1を解く際に得られた以下の式(複号同順)
\begin{aligned}
& x_{n-1} - x_{n} = \pm \frac{1}{q_{n-1} q_{n} } \\
& x_{n} - x_{n+1} = \mp \frac{1}{q_{n} q_{n+1} } \\
& -x_{n-1} + x_{n+1} = \mp \frac{1}{q_{n-1} q_{n+1} } \\
\end{aligned}において、 x_n を p_n で置き換えます (n \geqq 2 ) 。
\begin{aligned}
& \frac{p_{n-1}}{q_{n-1}} - \frac{p_{n}} {q_{n} } = \pm \frac{1}{q_{n-1} q_{n} } \\
& \frac{p_{n}}{q_{n}} - \frac{p_{n+1}} {q_{n+1} } = \mp \frac{1}{q_{n} q_{n+1} } \\
& - \frac{p_{n-1}}{q_{n-1}} + \frac{p_{n+1}} {q_{n+1} } = \mp \frac{1}{q_{n-1} q_{n+1} } \\
\end{aligned}各式の分母を払います。
\begin{aligned}
& q_{n} p_{n-1} - q_{n-1} p_{n} = \pm 1 \\
& q_{n+1} p_{n} - q_{n} p_{n+1} = \mp 1 \\
& - q_{n+1} p_{n-1} + q_{n-1} p_{n+1} = \mp 1 \\
\end{aligned}p_n の漸化式を求める
ここから、 p_n だけの式にしたいのですが、今度は辺々足しても、右辺は0にならないし、苦し紛れに1番目の式の両辺を2倍して、辺々足してみたらどうなるでしょうか。
\begin{aligned}
& (2q_{n}- q_{n+1}) p_{n-1} \\
&+(q_{n+1}- 2q_{n-1}) p_{n} \\
& +(- q_{n}+ q_{n-1}) p_{n+1}= 0
\end{aligned}右辺は0になるので、定数項は無くなりました。 p_n にかかる係数を何とかしなければなりませんが、とりあえず式(1)を使って、 q_{n+1} を消してみます。
\begin{aligned}
& \{2q_{n}- (q_{n} + q_{n-1}) \} p_{n-1} \\
&+\{ (q_{n} + q_{n-1})- 2q_{n-1} \} p_{n} \\
& +(- q_{n}+ q_{n-1}) p_{n+1}= 0
\end{aligned}q_n の項を整理すると、
\begin{aligned}
& (q_{n}- q_{n-1}) p_{n-1} \\
&+ (q_{n} - q_{n-1}) p_{n} \\
& +(- q_{n}+ q_{n-1}) p_{n+1}= 0
\end{aligned}おおっ!これは!! 式(1) から、 q_{n} - q_{n-1} = q_{n-2} ( n \geqq 2) であり、 q_{n-2} > 0(n \geqq 2) なので q_{n} - q_{n-1} > 0 です。よって、辺々を q_{n} - q_{n-1} で割って、
\begin{aligned}
& p_{n-1} + p_{n} -p_{n+1}= 0
\end{aligned}すなわち
\begin{aligned}
& p_{n+1}= p_{n} +p_{n-1} \text{ } \cdots (2)
\end{aligned}を得ます ( n \geqq 2 ) 。 なんと p_n も、フィボナッチ数列でした。
p_1 = q_1 x_1 = 1 \times 1 = 1 、 p_2 = q_2 x_2 = 2 \times \frac{1}{2} = 1 であることから、すべての n \geqq 1 に対し、 p_n が整数であることが逐次的に示せます。
なお、 p_0 = q_0 x_0 =1 \times 0 = 0 であることから、すべての n \geqq 0 に対し、 p_n は整数であることが示せました。また、式(2) は n \geqq 1 の範囲で成り立ちます。
p_n と q_n が互いに素であることの証明
背理法で証明します。
n=3 までの p_n と q_n の値は、以下の表1の通りです。
| n | q_n | p_n |
|---|---|---|
| 0 | 1 | 0 |
| 1 | 1 | 1 |
| 2 | 2 | 1 |
| 3 | 3 | 2 |
n=0,1,2 のとき、p_n と q_n が互いに素であると胸を張って言い切ってしまってよいのか、ちょっと気になりますが、 n =3 の時は明らかに互いに素です。
n \geqq 4 のとき、 p_{n} と q_{n} が互いに素でないとすると、ある自然数 m > 1 およびある自然数 p, q (p \ne q ) が存在して、
\begin{aligned}
& p_{n} = mp \\
& q_{n} = mq \\
\end{aligned}が成り立ちます。
一方、
q_{n-1}p_{n} - q_{n} p_{n-1} = \pm1が成り立つので、
mpq_{n-1} - mq p_{n-1} = \pm1となります。左辺を m でくくって、
m(pq_{n-1} - q p_{n-1}) = \pm1となりますが、自然数 m は1より大きく、また pq_{n-1} - q p_{n-1} は整数なので、この2つを掛けて \pm 1 になるというのは矛盾です。
したがって、 n \geqq 3 のとき、 p_{n} と q_{n} が互いに素で有ることが証明できました。
補足
\begin{aligned}
& q_{n} p_{n-1} - q_{n-1} p_{n} = \pm 1 \\
& q_{n+1} p_{n} - q_{n} p_{n+1} = \mp 1 \\
& - q_{n+1} p_{n-1} + q_{n-1} p_{n+1} = \mp 1 \\
\end{aligned}から p_n の漸化式を導出するとき、全部の式を使わずに、式1と式2の辺々を足すか、式1と式3の辺々を引いても、漸化式を導出できます。
たとえば式1と式2の辺々を足すと、
\begin{aligned}
& q_{n} p_{n-1} - q_{n-1} p_{n} \\
&+q_{n+1} p_{n} - q_{n} p_{n+1} = 0
\end{aligned}p_n の係数をまとめて
\begin{aligned}
& q_{n} p_{n-1} +(- q_{n-1}+q_{n+1}) p_{n} - q_{n} p_{n+1} = 0
\end{aligned}式(1) を代入して
\begin{aligned}
& q_{n} p_{n-1} + q_{n} p_{n} - q_{n} p_{n+1} = 0
\end{aligned}q_n > 0 なので、式(2) が導出できました。
こちらのほうが計算も少なくて、スマートです。式(1)をうまく適用できないか、という観点で考えていると、思いつけると思います。先に導出された結果を、後の論証に使えないかどうか、常に考えるようにしましょう。
小問3の解法
問題文が変に持って回った言い回しになっていますが、不等式
| x_{n+1} - \alpha | < \frac{2}{3} |x_{n} - \alpha |
を証明することで、 \lim_{n \to \infty} x_n = \alpha であることが示せます。
ここで表1を改めて見ると、明らかに p_n = q_{n-1} です。すなわち、
x_n = \frac{q_{n-1} } { q_n}です。ここで q_n の漸化式である式(1)を適用すると、
\begin{aligned}
& x_{n+1} = \frac{q_n}{q_{n+1}} \\
& \text{ } = \frac{q_n}{q_{n} + q_{n-1}} \\
& \text{ } = \frac{1}{1 + \frac{q_{n-1}}{q_n}} \\
& \text{ } = \frac{1}{1 + x_n}
\end{aligned}が成り立ちます。
したがって、
\begin{aligned}
&| x_{n+1} - \alpha | \\
& = \left | \frac{1}{1+ x_n} - \frac{1}{1+ \alpha} \right | \\
& = \frac{1}{(1+ x_n)(1+ \alpha) } |x_n-\alpha| \\
\end{aligned}
ですが、 x_n > 0 であることと \alpha =\frac{-1+\sqrt{5} }{2} であることから、
\begin{aligned}
& \frac{1}{(1+ x_n)(1+ \alpha) } < \frac{1}{1+ \alpha } \\
& \text{ } = \frac{1}{1+ \frac{-1+\sqrt{5} }{2} } \\
& \text{ } = \frac{2}{1+\sqrt{5} } \\
& \text{ } < \frac{2}{3}
\end{aligned}であるので
\begin{aligned}
&| x_{n+1} - \alpha | < \frac{2}{3} |x_{n} - \alpha |
\end{aligned}
が成り立ちます。したがって、
\begin{aligned}
&| x_{n} - \alpha | < \left ( \frac{2}{3} \right )^n|x_{0} - \alpha |
\end{aligned}
が成り立ちます。右辺は n \to \infty のとき0に収束するので、 \lim_{n \to \infty} x_n = \alpha が示せました。
発展 – その1:フィボナッチ数列の隣接項の比
フィボナッチ数列の隣接項の比 \frac{q_{n+1}} {q_n} はいわゆる黄金比 \frac{1+ \sqrt{5} }{2} に収束することが知られています。本ブログでも、「複素平面上のフィボナッチ数列 – 2001年東大 数学 第4問」という記事に、複素数版の証明を乗せていますので、ご覧ください。
小問3で、その逆数 \frac{q_{n}} {q_{n+1}} が収束することを示した \alpha = \frac{-1+\sqrt{5} }{2} は、正しく黄金比の逆数になっています。
発展 – その2:一般に p_n = q_{n-1} は成り立たない
小問3では、 p_n = q_{n-1} であることをうまく利用して、 x_n =\frac{q_{n+1}} {q_n} の収束を示しましたが、一般にこれは成り立ちません。
実際、以下のケースでは、 p_n = q_{n-1} にはなりません。
\begin{aligned}
& C_0 : x^2 + ( y- \frac{1}{2} )^2 = \frac{1}{4} \\
& C_1 : (x- \frac{1}{3})^2 + ( y- \frac{1}{18} )^2 = \frac{1}{324}
\end{aligned}n \leqq 3 の範囲の x_n,r_n,q_n, p_n の値は、以下の通りです。
| n | x_n | r_n | q_n | p_n |
|---|---|---|---|---|
| 0 | 0 | \frac{1}{2} | 1 | 0 |
| 1 | \frac{1}{3} | \frac{1}{18} | 3 | 1 |
| 2 | \frac{1}{4} | \frac{1}{32} | 4 | 1 |
| 3 | \frac{2}{7} | \frac{1}{98} | 7 | 2 |
p_n \ne q_{n-1} のとき、小問3の証明は面倒くさくなります。そもそも \alpha に収束するかどうかも、定かではありません。出題者は受験者が変に泥沼に陥らないように、問題を設定していることがわかります。
発展 – その3: p_n \ne q_{n-1} のときの小問3
p_n \ne q_{n-1} のとき、 x_n = \frac{p_n}{q_n} が何に収束するか、考察してみます。
q_n, p_n の一般項
ちょっとダサいですが、 q_n, p_n の一般項を求めます。
方程式
x_2-x-1=0
の2つの解を、 \phi, \psi (\psi < \phi ) と置きます。大きいほう \phi が、黄金比です。
3項数列の一般項を求めるやりかたで、普通に導出できますが、昔も今も教科書にきちんと説明が載っていないので、一般項の求め方を少し詳しく記述します。
q_n が満たす漸化式は
q_{n+1} -q_n - q_{n-1} = 0ですが、解と係数の関係より、
\begin{aligned}
& \phi + \psi = 1 \\
& \phi \psi = -1
\end{aligned}なので、これを漸化式の係数に代入して
q_{n+1} -(\phi + \psi )q_n +\phi \psi q_{n-1} = 0を得ます。これを変形して
\begin{aligned}
& q_{n+1} -\phi q_n = \psi (q_n - \phi q_{n-1}) \\
& \text{ }= \psi^n (q_1 - \phi q_{0})
\end{aligned}が成り立ちます。同様に、
\begin{aligned}
& q_{n+1} -\psi q_n = \phi^n (q_1 - \psi q_{0})
\end{aligned}が成り立ちます。
1つ目の式の両辺に \psi を、2つ目の式の両辺に \phi をそれぞれかけて、
\begin{aligned}
& \psi q_{n+1} -\phi \psi q_n = \psi^{n+1} (q_1 - \phi q_{0}) \\
& \phi q_{n+1} -\phi \psi q_n = \phi^{n+1} (q_1 - \psi q_{0})
\end{aligned}辺々引いて
\begin{aligned}
& (\psi - \phi) q_{n+1} = \psi^{n+1} (q_1 - \phi q_{0}) \\
& \text{ } - \phi^{n+1} (q_1 - \psi q_{0})
\end{aligned}整理すると
\begin{aligned}
&q_{n} = \frac{1}{\phi - \psi } \{ ( \phi^{n} - \psi^{n}) q_1 \\
& \text{ }- \phi \psi ( \phi^{n-1} - \psi^{n-1}) q_{0}) \}\\
\end{aligned}ここで
\begin{aligned}
& \phi - \psi = \sqrt{5} \\
& \phi \psi = -1
\end{aligned}を代入して、
\begin{aligned}
&q_{n} = \frac{1}{\sqrt{5} } \left \{ ( \phi^{n} - \psi^{n}) q_1 + ( \phi^{n-1} - \psi^{n-1}) q_{0} \right \}\\
\end{aligned}同様に、
\begin{aligned}
&p_{n} = \frac{1}{\sqrt{5} } \left \{ ( \phi^{n} - \psi^{n}) p_1 + ( \phi^{n-1} - \psi^{n-1}) p_{0} \right \}\\
\end{aligned}x_n の一般項と極限
x_n = \frac{p_n}{q_n} の一般項は
\begin{aligned}
& x_n = \frac{p_n}{q_n} \\
& = \frac{ ( \phi^{n} - \psi^{n}) p_1 + ( \phi^{n-1} - \psi^{n-1}) p_{0} }{ ( \phi^{n} - \psi^{n}) q_1 + ( \phi^{n-1} - \psi^{n-1}) q_{0} }\\
& = \frac{ \{ \phi - \psi ( \frac{\psi}{\phi})^{n-1} \} p_1 + \{ 1 - ( \frac{\psi}{\phi})^{n-1} \} p_{0} }{ \{ \phi - \psi ( \frac{\psi}{\phi})^{n-1} \} q_1 + \{ 1 - ( \frac{\psi}{\phi})^{n-1} \} q_{0} }\\
\end{aligned}となります。ここで、
\begin{aligned}
& \left |\frac{\psi }{\phi } \right | = \left |\frac{3 - \sqrt{5} }{2} \right | < 1
\end{aligned}なので、 \lim_{n \to \infty} \frac{\psi }{\phi } = 0 が成り立ちます。したがって、
\begin{aligned}
& \lim_{n \to \infty}x_n = \frac{ \phi p_1 + p_{0} }{ \phi q_1 + q_{0} }\\
\end{aligned}となります。 x_n が \alpha に収束するのは、特殊なケースであることがわかりました。
逆に、 p_n,q_n を整数にすることにこだわらなければ、初期値をうまくコントロールすることで、 x_n を比較的自由な値に収束されることが出来ます。たとえば、初期値を以下のように設定すると、 x_n を \frac{1}{2} に収束させることができます。
| n | x_n | r_n | q_n | p_n |
|---|---|---|---|---|
| 0 | 0 | \frac{1}{2} | 1 | 0 |
| 1 | \frac{1}{1+ \phi} | \frac{1}{4+6 \phi} | 1+ \phi | 1 |
| 2 | \frac{1}{2+ \phi} | \frac{1}{10+10 \phi} | 2+\phi | 1 |
| 3 | \frac{2}{3+ 2\phi} | \frac{1}{20+14 \phi} | 3+ 2\phi | 2 |
発展 – その4: p_n と q_n が互いに素である件
フィボナッチ数列の隣接項が互いに素であるというのも、良く知られていますが、本問の小問2はまさにその証明を求めています。しかし本稿では、 p_n = q_{n-1} であることを使わずに証明できたので、 p_n \ne q_{n-1} のときも互いに素であることがわかります。
解法のポイント
本問は登場する変数が多い( x_n,r_n,q_n,p_n の4種類)ので、どのようにして変数を減らし、欲しい変数だけの式にするかがポイントです。
最初に3平方の定理を使って3つの式が出来た時に、右辺、左辺と変数を分離することが1番目のポイントです。次いで、左辺側の x_n が3式合わせると対称式のように循環していて、しかもマイナスの項があることに注目です。うまくすると、今回のように辺々足したらキャンセルしあって0、ということが期待できます。
一般には代入法で変数を減らしますが、条件がそろえば一気に消せるので、その可能性を常に探ってください。
p_n = q_{n-1} に気が付くことも重要です。これに気が付かないと、小問3がえらく大変になります。
入試問題というものは過度に泥沼状態に陥らないよう、今回の p_n = q_{n-1} のように、スマートに解けるように特殊な条件を前提としていることが、往々にしてあります。問題を解いていてドロドロになりかけたら、スマートな解決に導く「蜘蛛の糸」が天井からぶら下がっていないか、今一度設問内容を確認してみてください。
面倒な計算を避けてパパっと答えを導けないか、常に考え続けることがポイントです。
