キングオブ難問 – 1998年東大数学後期第3問

2021年5月3日2023年12月11日

　数学の大学入試問題で、史上最強と言われているのが、 1998年東大数学後期第3問です。難しすぎて試験当日に、予備校が解答速報を出すことが出来なかった、という逸話が残るほどの超難問です。今日に至るまで、その隔絶した難しさに迫る入試問題は現れていません。

　異様とも言えるオーバーキル的超絶難易度の本問。まさに難問の王と呼ぶにふさわしいですが、本稿ではその解法を、順を追って解き明かしていきます。

1998年東大数学後期第3問とは

　問題文が相当長いので、引用は断念しました。ググると問題文の画像がヒットしますので、そちらをご覧ください。

　問題の要旨ですが、側面に竹ひごをぷすぷす刺せる、オセロの駒をイメージしてください。このオセロの駒に、竹ひごで別のオセロの駒をつなぎます。１つのオセロに、何本でも竹ひごを刺せるものとします。

　オセロの追加方法には、以下の2種類があります。

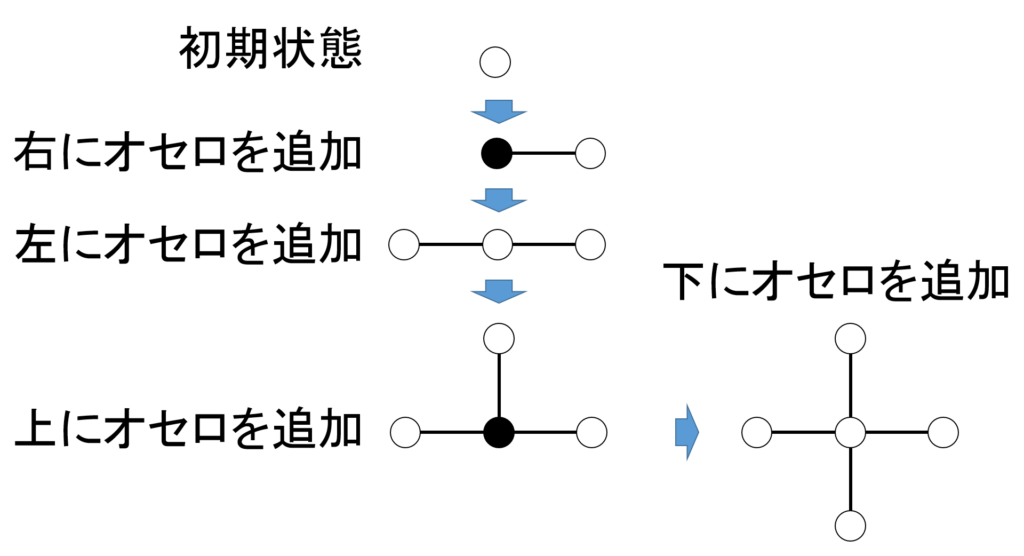
　オセロ列の一番端に、新しく白オセロを追加します。追加された側のオセロは、色を反転させます。

　オセロとオセロの間に、新しい白オセロを挿入します。もともとあった、両隣のオセロは色を反転させます。

　要は、新規追加のオセロは白、追加されたオセロに隣接するオセロは色を反転させる、というルールです。

　初期状態は、白のオセロの駒が１つだけです。これに上記の要領で、竹ひごとオセロをどんどんつないでいきます（図1参照）。

　この問題には、小問が2つあります。小問1は、以下の図2（オセロの駒が全部白）が生成できることを示せ、というものです。小問2は、図3のようにオセロを1列につないで、しかもオセロが全部白の時の、オセロの数が満たす条件は何か、というものです。

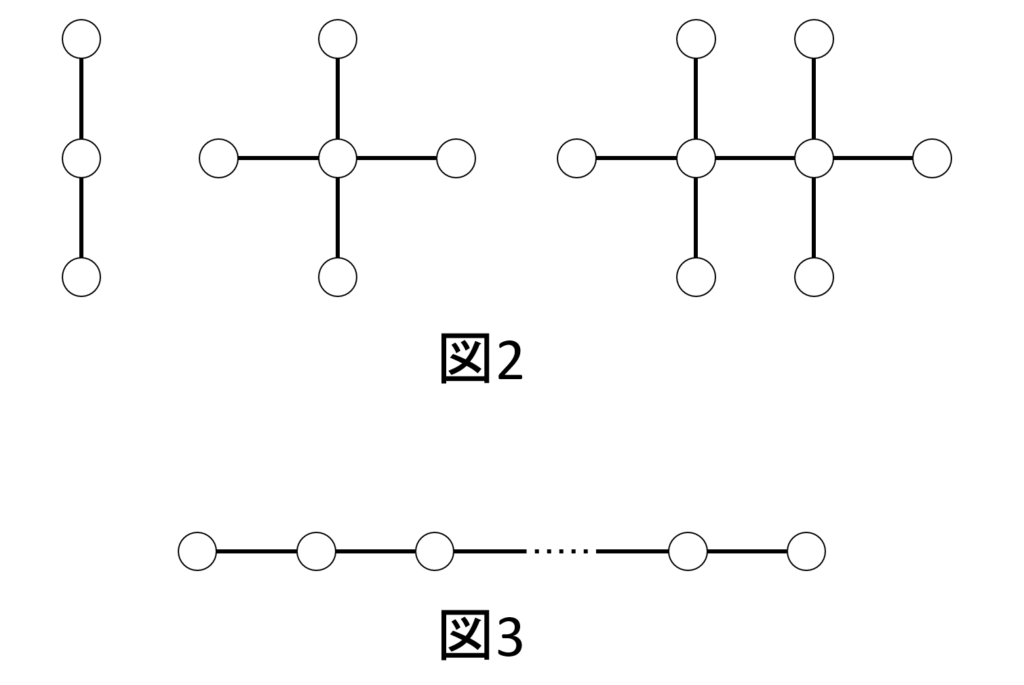
　史上最強だというのに、微積分もベクトルも行列も複素数も確率も出てきません。マッチ棒のパズルみたいな簡単な道具立てを使って、純粋に論理的思考力を問う内容となっています。

　グラフ理論というのは、一口で言うと巡回セールスマン問題のような数学的題材を扱う分野のことです。

　本問の問題文で、本稿におけるオセロ列を「グラフ」と呼んでいることから、本問とグラフ理論との関連を取り沙汰されることも有りますが、もちろん入試問題なので、グラフ理論に関する一切の知識は前提とされていません。

　要は、特に気にしなくて良いということです。

　超絶難問と言いながら、実は小問1は単なるパズルです。頭の体操的に楽しく解けます。本問のように問題文が長くて複雑な場合、小問1は設問を理解させるための例題的な位置づけであることが多いので、一応チェックして取りこぼしの無いようにしましょう。

　小問1は小問2以降のヒントであるという経験則がありますが、本問もその例にもれません。ですので、まずは、小問1の解き方が何か役に立たないか、という観点からアプローチしてみます。

　すると、小問1の図2一番右の図形の解き方が、役に立ちそうです。実際、以下の命題を導出できます。

n個の白オセロが1列に並ぶとき、n+3個の白オセロ列を生成することができる

「何かが出来る」とか、「何かが存在する」といった命題の証明は、その「何か」に関する具体例が示せればよいので、実際の試験では、以下の図4を使って説明すればOKです。

小問1で、 n=3 （図2の一番左）および n=4 （図2の一番右）のときに、白オセロ列ができることがわかっているので、命題１から、nが3で割り切れるまたはnを３で割った余りが１の場合は、白オセロ列ができることが示せました。