等面四面体の問題 – 1999年京大 理系 後期 第4問

2021年11月15日2023年2月28日

1999年京大 理系 後期 第4問 は空間図形の問題です。問題文は以下の通りです。

△ABC は鋭角三角形とする。このとき、各面すべてが △ABC と合同な四面体が存在することを示せ。

　京大の入試にはよく、「そんな訳ないだろ」的な問題が出題されますが、本問もその系譜です。題意が真であると、にわかには信じられません。

解法その１(図形的アプローチ）

△ABCを描いてみる

　とりあえず、鋭角三角形を描いてみます(図1)。

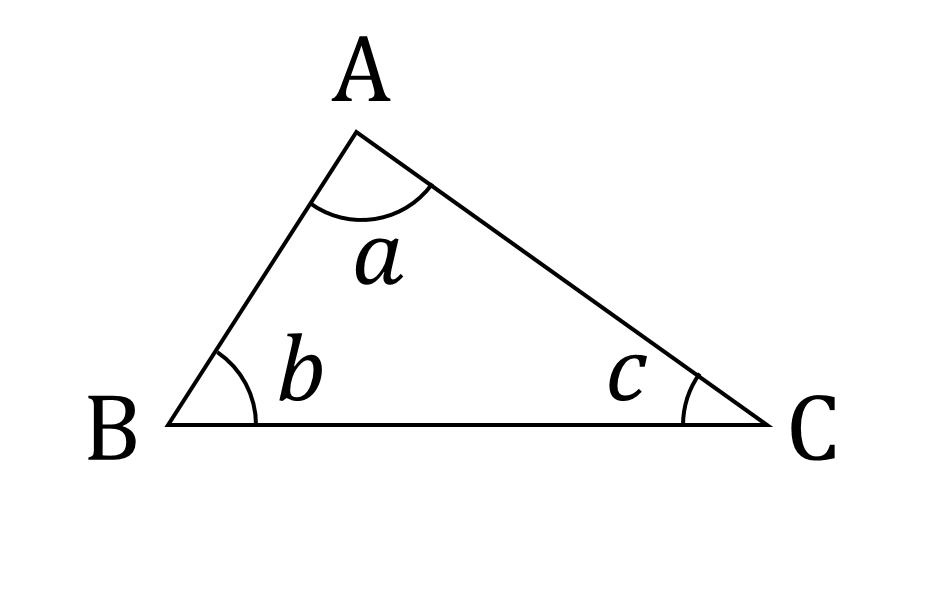
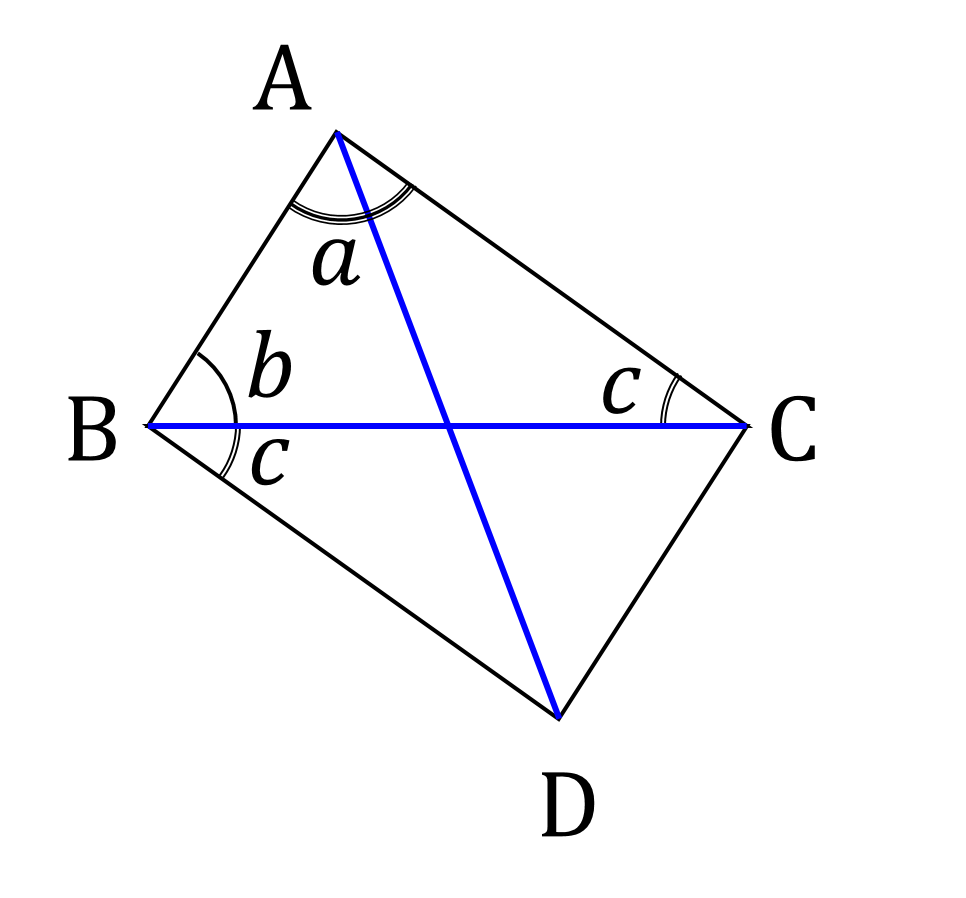
　図1において、各頂点の角度を、以下のように定義しておきます。

\begin{aligned}
& a = \angle \mathrm{BAC} \\
& b = \angle \mathrm{ABC}  \\
& c = \angle \mathrm{BCA}  \\
\end{aligned}

　どうやったら △ABC と合同な面だけで出来た四面体が出来るか考えるため、まずは △ABC と合同な三角形を、辺 BC を共有するように、配置してみます(図2)。

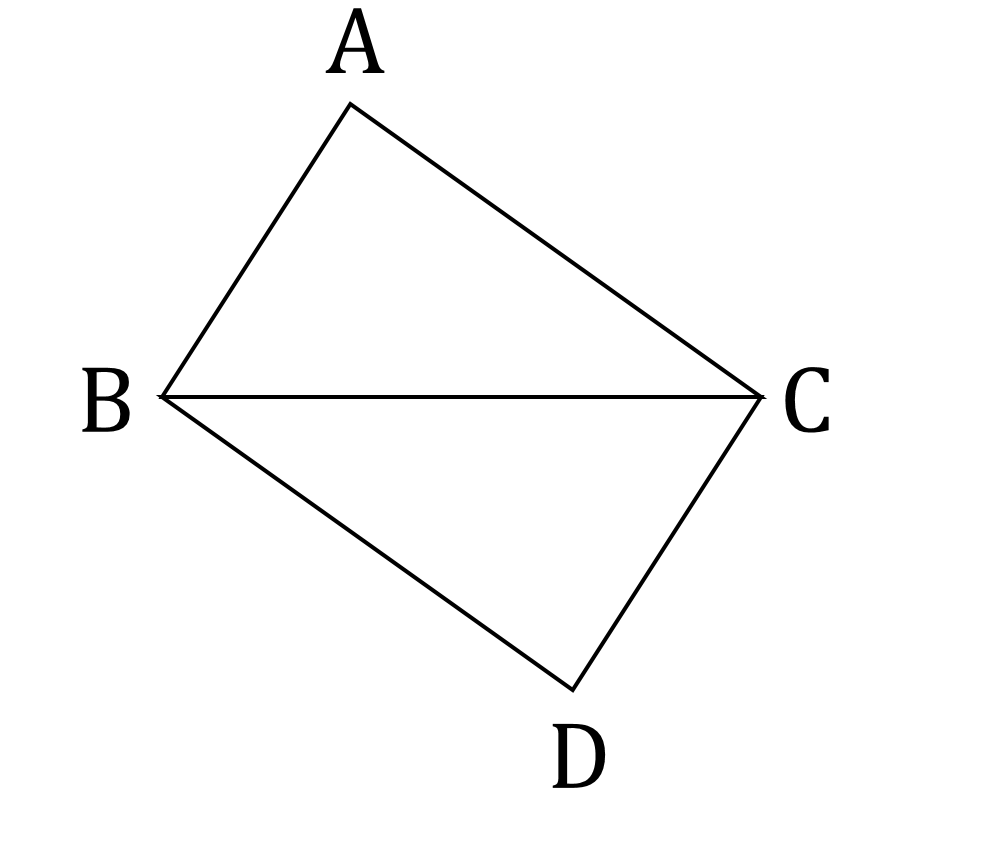
　すぐに気が付くことは、四角形 ABDC は平行四辺形であることですが、それはとりあえず置いておきます。

辺BCで折り曲げてみる

　ここで、図形が描かれた平面を、辺BC で折り曲げてみることをイメージします。すると、 AD の長さは折り曲げた角度 \theta の連続関数なので、 \theta をうまく調整すれば AD = BC とできるはずで、このとき四面体 ABDC は確かに等面四面体になります(図3)（おおっ！）。

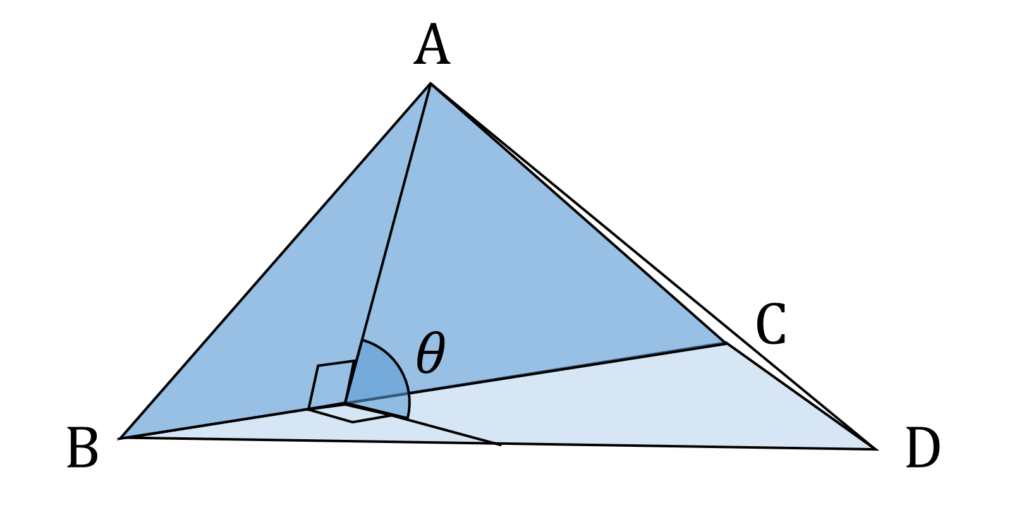
　時間がないときには、上記の内容をつらつら記述しても、原理は正しいのでそこそこの点数はもらえると思います。

　あとは、AD が \theta の連続関数であることを示し、中間値の定理を適用して AD = BC と出来ることを証明します。

平行四辺形ABDCにおいて BC < AD を示す

　平行四辺形 ABDC において、 △ABC は鋭角三角形なので、頂点 A から辺 BC に向けて下した垂線の足は、 BC 上にあります。これを H と置きます。また、 D から BC に下した垂線の足を I と置きます。

　さらに、

\begin{aligned}
 h &= \mathrm{AH} \\
 l &= \mathrm{HI} \\
\end{aligned}

と置きます(図4)。

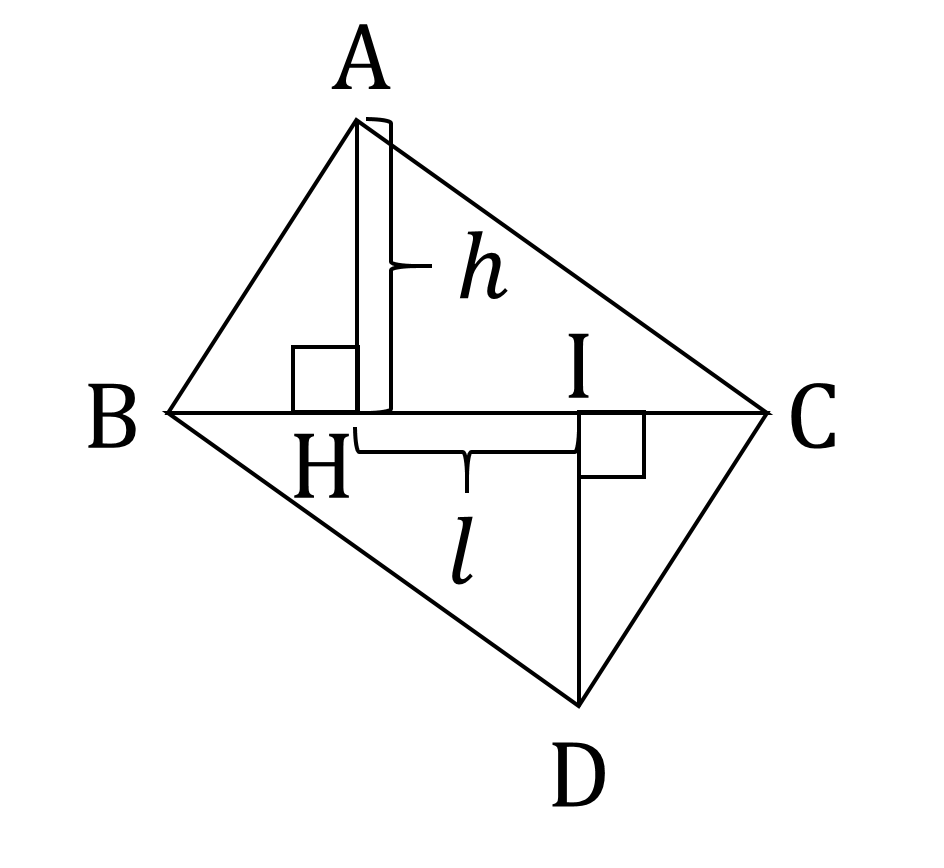
　このとき、

\begin{aligned}
 & \mathrm{BC}^2 \\
 & = \mathrm{AB}^2 +\mathrm{AC}^2 -2 \mathrm{AB} \cdot \mathrm{AC} \cos a \\
\\
&  \mathrm{AD}^2 \\
&= \mathrm{AB}^2 +\mathrm{DB}^2 -2 \mathrm{AB} \cdot \mathrm{DB} \cos (b+c) \\
& = \mathrm{AB}^2 +\mathrm{AC}^2 -2 \mathrm{AB} \cdot \mathrm{AC} \cos (\pi - a) \\ 
& = \mathrm{AB}^2 +\mathrm{AC}^2 +2 \mathrm{AB} \cdot \mathrm{AC} \cos a
\end{aligned}

ですが、△ABCは鋭角三角形なので、 \cos a > 0 です。したがって、

BC² < AD²

が成り立ちます(図5)。

　ところが、図4から明らかなように、

\mathrm{AD}^2 = 4h^2 + l^2

なので、

\mathrm{BC}^2 < 4h^2 + l^2

が成り立ちます。

辺BCで折り曲げた空間図形において、ADが \theta の連続関数であることを示す

　次に、図6において、 AD² は以下の式で表すことが出来ます。

\mathrm{AD}^2 = 2h^2 (1 -\cos {\theta} ) +l^2

　すなわち、 AD² は（ADも） \theta の連続関数です。

中間値の定理を適用して等面四面体が出来ることを示す

　 0 \leqq \theta \leqq \pi のとき、AD² の値の範囲は

0 \leqq \mathrm{AD}^2 \leqq 4 h^2 + l^2

ですが、 0 < \mathrm{BC}^2 < 4h^2 + l^2 なので、中間値の定理により、ある 0 < \theta_0 < \pi が存在して

 \mathrm{AD}^2 = 2 h^2(1 -\cos {\theta}_0 ) + l^2 = \mathrm{BC}^2

が成り立ちます。このとき四面体 ABDC は確かに等面四面体になります。

解法その2（直方体に内接する等面四面体が存在することを利用する)

　任意の直方体には、等面四面体が内接しているという性質が知られています。図7において、四面体P-RUW は等面四面体です。

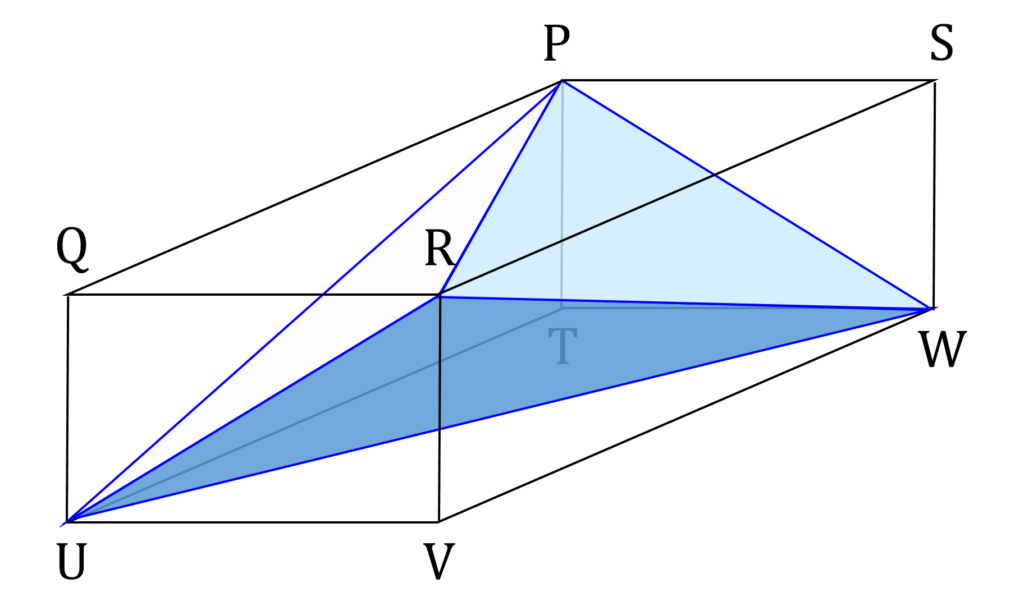
　図7において、直方体に内接する四面体の各辺は、直方体の各面の対角線になっています。そこで、鋭角三角形ABCが任意に与えられたとき、三角形の各辺の長さが各面の対角線になる直方体を構築できれば、内接する四面体は各面が△ABCに合同な等面四面体になります。

　鋭角三角形ABCが与えられたとき、各辺の長さを

\begin{aligned}
 \alpha &= \mathrm{AB} \\
\beta &= \mathrm{BC} \\
\gamma &= \mathrm{CA} \\
\end{aligned}

と置きます。

　連立方程式

\left \{ 
\begin{aligned}

  x^2 + y^2  &= \alpha^2 \\
 y^2 + z^2  & = \beta^2 \\
 x^2 + z^2  & = \gamma^2 \\

\end{aligned}
\right . \cdots(1)

を x^2, y^2, z^2 について解くと、

\begin{aligned}
& x^2 = \frac{\alpha^2 - \beta^2 +  \gamma^2 }{2} \\
& y^2 = \frac{\alpha^2 +\beta^2-  \gamma^2 }{2} \\
& z^2 = \frac{-\alpha^2 + \beta^2 + \gamma^2 }{2} \\
\end{aligned}

となりますが、△ABCは鋭角三角形なので、

\begin{aligned}
 &\alpha^2   +  \gamma^2 > \beta^2 \\
& \alpha^2 +\beta^2>  \gamma^2  \\
&  \beta^2 + \gamma^2 > \alpha^2 \\
\end{aligned}

が成り立ちます。したがって、連立方程式(1)は正の実数解

\begin{aligned}
& x = \sqrt{\frac{\alpha^2 - \beta^2 +  \gamma^2 }{2} } \\
& y = \sqrt {\frac{\alpha^2 +\beta^2-  \gamma^2 }{2} } \\
& z = \sqrt{ \frac{-\alpha^2 + \beta^2 + \gamma^2 }{2} } \\
\end{aligned}

を持ちますが、この x,y,z を縦、横、高さとする直方体に内接する等面四面体は、各面が△ABCと合同になります。

　ゆえに、各面すべてが △ABC と合同な四面体が存在することを示せました。

解法のポイント

　直方体に等面四面体が内接するというのは、割と良く知られているようなので、これを知っていれば、解法その2のやり方で、比較的容易に解くことが出来ます。

　それを知らなかった場合は解法その1の手法で攻めることになりますが、空間図形の存在証明問題において、本稿のように、２つの平面の成す角をいろいろ動かすことをイメージしてみるというのは、結構使えます（2008年京大乙第3問）。類似の問題に出くわしたら、試してみてください。