2001年東大 数学 後期 第3問 は、級数和の極限の問題です。問題文は以下の通りです。
整数を係数とする2次多項式 f(x) で2次の項が正のものが与えられている。任意の実数 x に対して、平面上の原点を中心とし半径が1である単位円 C 上の点 P(x) を
P(x) = ( \cos 2\pi f(x), \sin 2\pi f(x) )
によって定める。円周 C の弧 I で長さが L (0 < L < 2\pi) であるものを固定する。そのとき各自然数 k に対して区間 [k,k+1] の部分集合
\{ x | k \leqq x \leqq k+1, P(x) \in I \}
は互いに交わらない有限個の区間の和集合になっているので、それらの区間の長さの総和を T_k であらわす。このとき
\displaystyle\lim_{k \to \infty} T_k = \displaystyle\frac{L}{2\pi}
を証明せよ。
まず、何を言っているのか理解するのが一苦労です。放り出したい気分になりますが、後期なのでそんなわけにいきません(ほかの問題も難しいに違いない)。ここはおとなしく、腰を据えて取り組みます。
2001年東大 数学 後期 第3問 の定式化
まず、問題文の意味するところを、数学で扱いやすいように整理します。
2次の整式 f(x) を
f(x) = a x^2 + bx +c
と置きます。ここに a,b,c は整数で、 a > 0 です。 x が十分に大きい範囲を問題にしているので、 f(x ) は単調増加関数として問題ありません。
問題文の内容から見て、 y = f(x) の逆関数 x = f^{-1} (y) の具体的な式が必要になりそうなので、それを求めます。二次方程式の解の公式より、
x = f^{-1}(y) = \frac{-b+ \sqrt{D+4ay}}{2a}です。ここに D = b^2 -4ac です。また、 x は十分に大きいとして問題ないので、二次方程式の解の公式の平方根についている \pm のうち、+の方だけを考えます。また、 f^{-1} ( y) は単調増加関数です。
ここで、弧 I の端点の偏角を \alpha, \beta ( \alpha < \beta \leqq 2 \pi ,\beta -\alpha = L) と置きます。 P(x) や C が XY 平面上に在るとして、そのイメージを図示すると、図1のようになります。
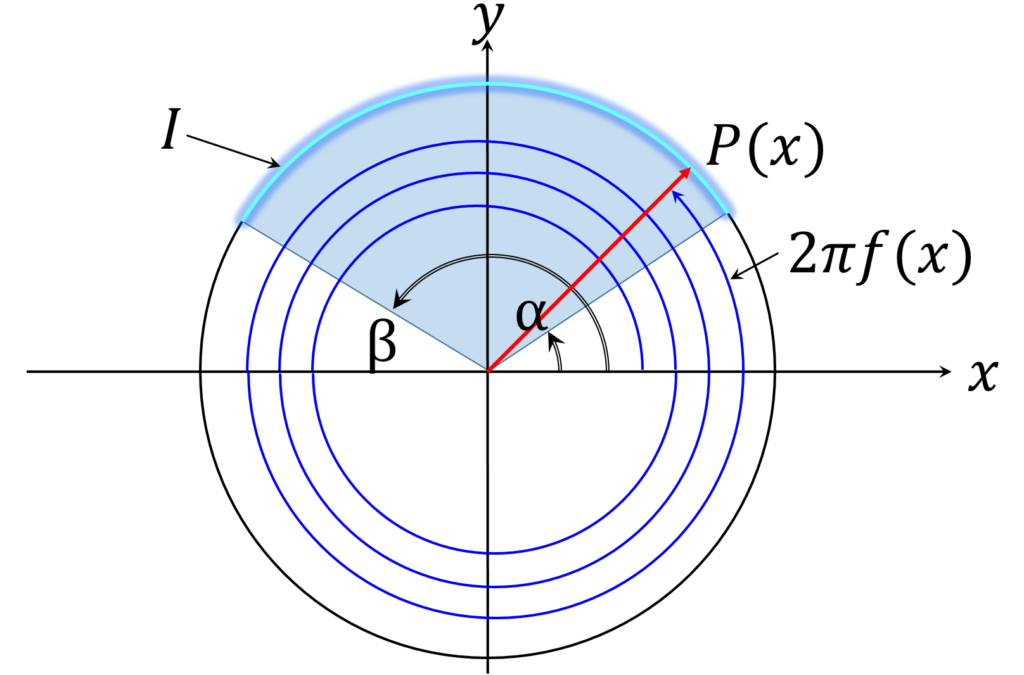
x が k から k+1 までを動くとき、 P(x) は原点の周りを f(k+1) -f(k) = 2ak + a + b 回まわります。したがって P(x) は I を 2ak + a+ b 回通ります。
