2023年の千葉県公立高校入試(数学)は、昨年と比べると多少易しくなった感がありますが、今や千葉県名物と言える(嘘)ポイズンピル問題(他と不釣り合いな難問のため、拘泥するとえらいことになる)は、今年も健在です。
2022年のポイズンピル問題は二次関数から出題されていましたが、今年は以前のパターンに戻って、図形問題です。そのため、過去問を研究していれば、これは怪しそうだと見ぬくことが出来たかもしれません。
どのような問題なのか、早速見ていきましょう。
2023年 千葉県 数学 第3問とは
問題文は以下のリンク先をご覧ください。
本問は円に関する図形の問題です。
図1のように、円Oの直径BCの延長上に点Aがあり、また、円周上に点Dと点Eがあります。
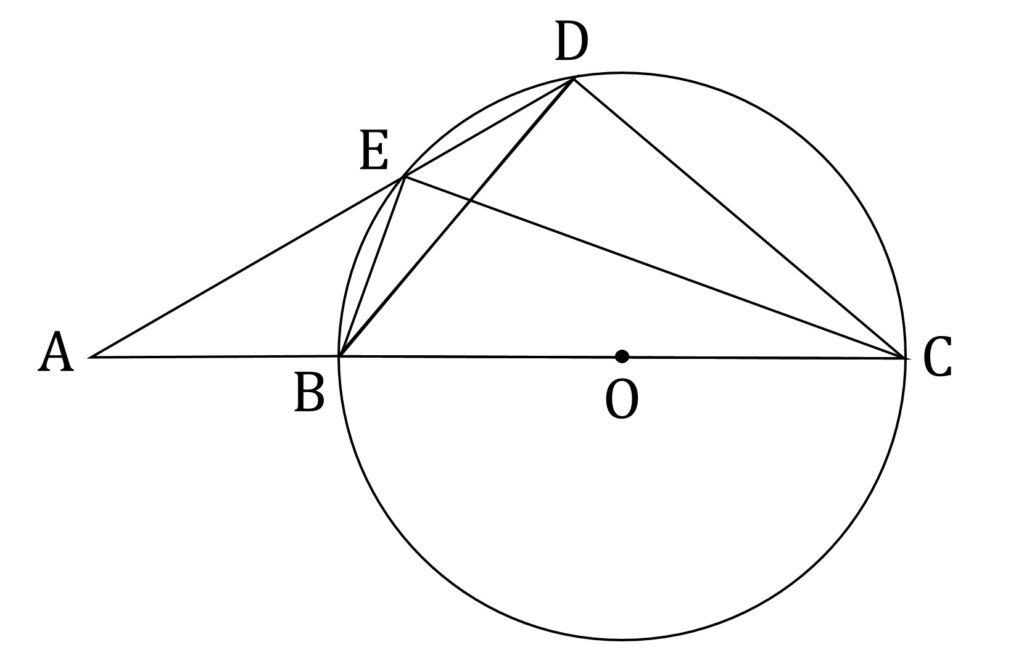
これに関して小問が3つ用意されていて、小問1は直径を見込む円周角の大きさを聞く問題(言うまでもなく90度!)、小問2は△ABE ∽ △ADC を証明する問題です。小問1はボーナス問題、小問2も教科書レベルの超基本問題です。しっかり得点しておきましょう。
鬼畜度マシマシの小問3
小問3は、Eを通り線分ADと垂直な直線が、線分BCおよび線分BDと交わる点をそれぞれ、F、Gとし、
\rm{EG}=1cm,GF=2cm,\angle A = 30 \degreeのとき、AB の長さをもとめよ、というものです(図2)。
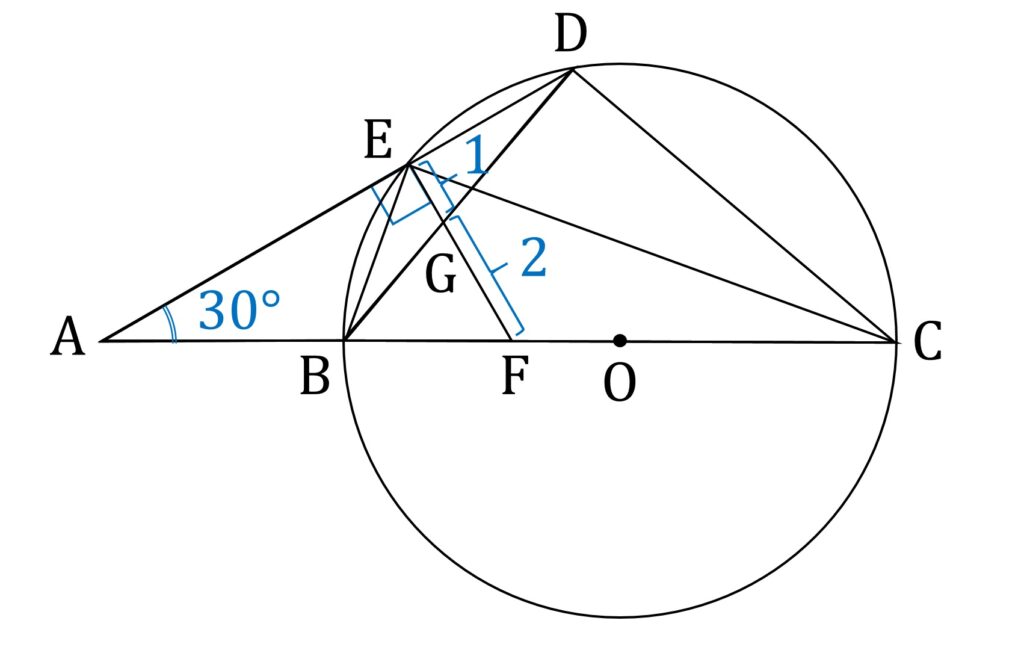
一見して、どうということのない問題に見えます。小問1、小問2の余勢を駆って、一気に解いてしまおうと突っ込むと、島津義久の釣り野伏にまんまと引っかかり、罠だと気づいた時には、回答時間を無為に空費するはめに陥っています。そういう意味でも、本問は実に凶悪です。
小問3の解法
辺の長さが与えられたら相似比、相似比と言ったら平行線だ!というわけで、補助線を引いて平行線を生み出します。
点Bから線分ADに垂らした垂線の足をHと置くとき、HB//EF です(図3)。
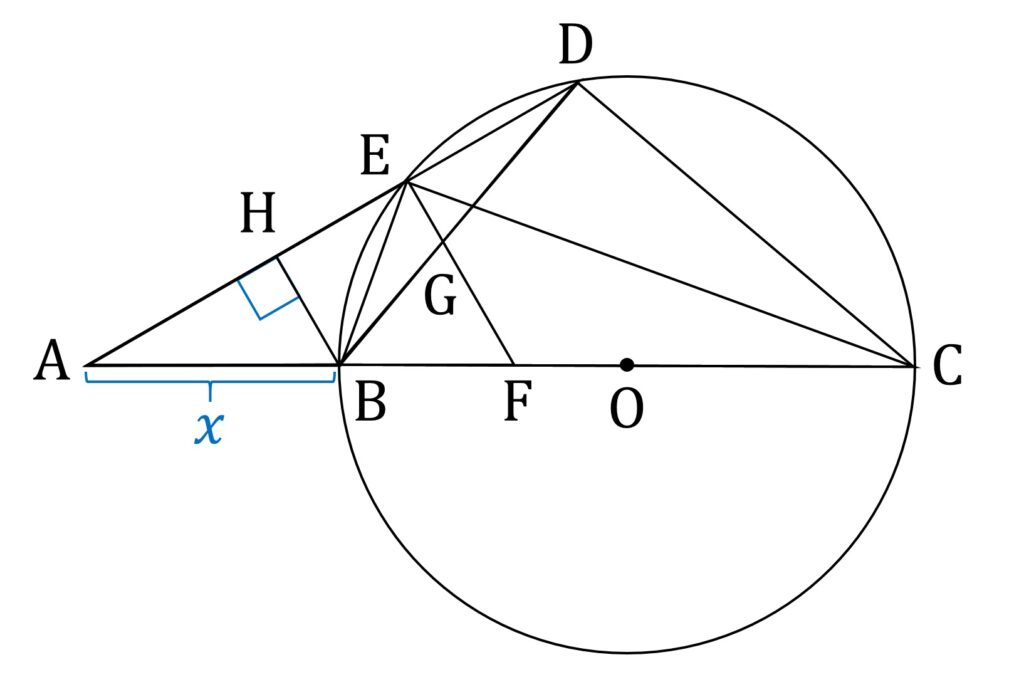
\mathrm{AB} = xと置くとき、△AEF は三角定規型三角形であり、 EF= 3 なので、
\mathrm{BF} = 6 -xです。このとき、 \rm{AF : AE} = 2 : \sqrt{3} なので、
\mathrm{HE} = \frac{ \sqrt 3} 2 (6 -x)です。
一方、HB // EG かつ HB= \displaystyle\frac{x} 2 ,EG = 1 なので、
\begin{aligned}
\mathrm{HE :ED } & = \frac{x}2 -1 :1 \\
& =x-2 :2
\end{aligned}です。
よって、
\mathrm{ED}= \frac{2}{x-2} \mathrm{HE} = \frac{ \sqrt 3 (6 -x) }{x- 2}を得ます。
これから、
\begin{aligned}
\rm{AD} & = \rm{AE + ED } \\
&= 3\sqrt3 + \frac{ \sqrt 3 (6 -x) }{x- 2} \\
& =\frac{ 3\sqrt 3 x }{x- 2}
\end{aligned}が成り立つので、△ABE と△ADC の相似比は
x: \frac{ 3\sqrt 3 x }{x- 2} = 1 : \frac{ 3\sqrt 3 }{x- 2} です。
よって、AC を求めることが出来、そこから AB の長さ x を引いて BC の長さを求めることが出来ます。
更に、△BHE が直角三角形なので、 BF の長さを三平方の定理で求めることが出来、ここから相似比を使ってDC の長さを求めます。
△DHB も直角三角形なので、三平方の定理を使って BD の長さを求めることが出来ます。
最後に、 △DBC も直角三角形なので、三平方の定理により \rm{ BD^2 + DC^2 = BC^2} です。これにここまでの結果を代入して、 x の方程式を得ます。
これを解くことで、 AB の長さを求めることができるはずですが、問題は、出来上がった式が x の4次方程式になってしまうことです。
高校の履修範囲で高校入試を解かせるなど、いくら何でも鬼畜度が過ぎます。つまり、このアプローチではないということです。 x の次数が高くなってしまうのは3平方の定理を利用したからなので、これを使わない解き方を考えます。
小問3の【真の】解法
3平方の定理を封印するなら、使える手段は相似しかありません。そこで、相似の関係にある三角形で、かつ長さがわかっている線分EG,GF,EFを含むものを探します。
ここで、 △DEG ∽ △CEB であることに気がつくことが、第1歩です。実際、2つの三角形は直角三角形で、かつ同一弧上の円周角は等しいことから ∠EDG = ∠ECB が成り立つので、確かに相似です(図4)。
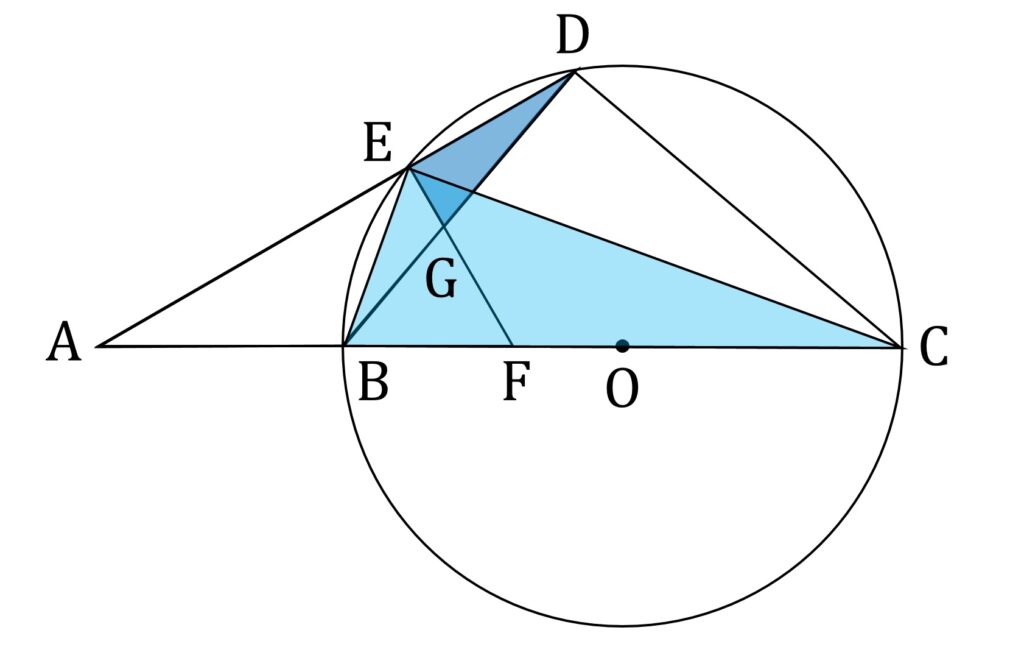
そのうえで、 △EBF ∽ △BGF であることに気がつくことが、決定的に重要です。
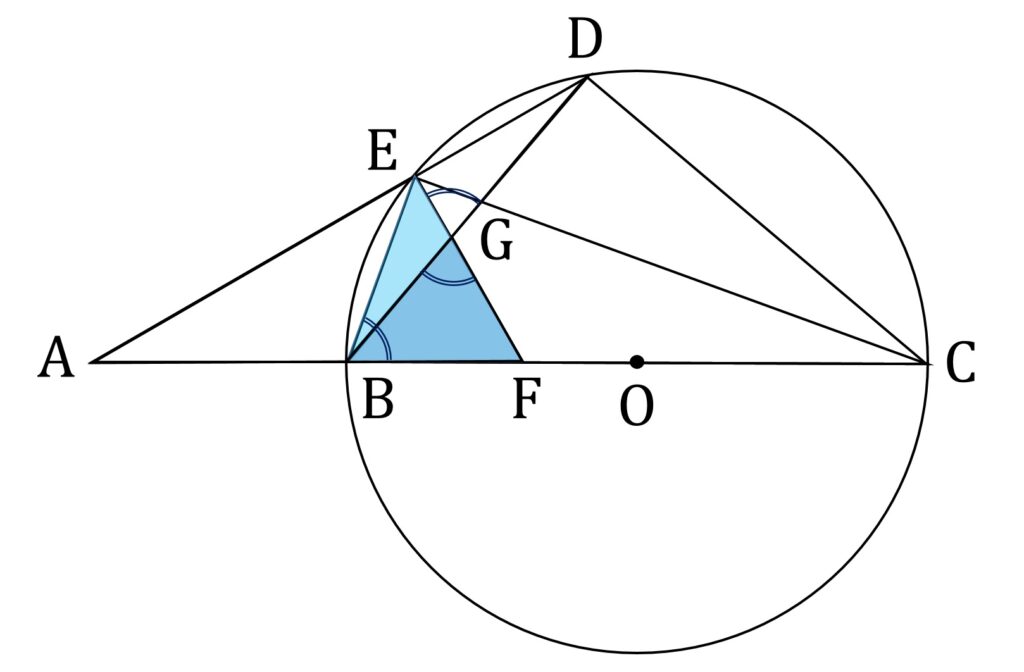
△DEG ∽ △CEB であることから、
\angle \mathrm{EBF} = \angle \mathrm{EGD} ですが、対頂角の関係にあるので
\angle \mathrm{EGD} = \angle \mathrm{BGF} です。よって、
\angle \mathrm{EBF} = \angle \mathrm{BGF} が成り立ちます。
一方、明らかに
\angle \mathrm{BFE} = \angle \mathrm{GFB} です(2角は同じもの)。
したがって、 △EBF ∽ △BGF なので、
\rm \frac{FB}{FE} = \frac{FG}{FB}です。ところが、 \mathrm{ AB }= x とおくとき、
\mathrm {FB} = 6-xであり、かつ
\rm FE = 3,FG=2
なので、
\frac{6-x}{3} = \frac{2}{6-x}です。これより方程式
x^2 -12x + 30 = 0
を得ますが、 x < 6 なので
x = 6 - \sqrt{6} \text{ } \rm (cm)です。単位を付け忘れないよう、気をつけましょう。
解法のポイント

本問を解くにあたってのポイントは
- 三平方の定理を使わないようにする
- △EBF ∽ △BGF に気づく
です。
これだけ直角三角形が出てくるのに、三平方の定理を使わずになんとかしようと言う発想に至るのは、なかなかハードルが高いと言えます。これに加えて、2点目の相似です。
これに気がつくのも結構大変なうえに、思わせぶりに登場する ∠A = 30° と言う条件が、回答者をミスリードするだけで回答には不要であるというのも、相当な意地悪です。本問の難易度はやはり尋常とは思えません。
ことし(2023年)の大学共通テストの数1Aに、中学の知識だけで解ける図形の問題が出題されていました(大問5)。数1Aの中でも難しい部類の問題でしたが、それと比べても本問の難易度は隔絶しています。
そんな難問にもかかわらず、配点は高々5点です。本問が解ける人が、そんなにホイホイいるはずもないので、本問に拘泥するより、他の問題の完璧を期すほうが、受験戦略上は正しいでしょう。特に数学が得意な人にとっては、満点を取ろうと気張ってしまいがちなところですが、「山頂を目前に登頂を断念する勇気」的なものも問われている、そんな問題でした。
