不定積分がわからないのに積分値の整数部分を出せ・・だと?! 2023年東工大 数学 第1問

2023年東工大 数学 第1問 は積分の問題です。問題文は以下のとおりです。
実数 \displaystyle{\int_0 ^{2023} \frac{2}{x + e^x} dx } の整数部分を求めよ。
シンプルな問題文ですが、この手の問題のほうがヤバイことが往々にして有ります。実際、 \displaystyle{\frac{2}{x + e^x} } の不定積分がわからないので(それとも導出できるのか?)、その定積分の整数部分など、どうやって求めるのか見当もつきません。
そうは言っても、積分挟み撃ちとか使えば何とかなるかも知れないので、見ていくことにします。
なお、以降の内容は東工大が公表したものではありません。
2023年東工大 数学 第1問 の解法
積分挟み撃ちで攻めて見る
そんな訳で、まずは積分挟み撃ちです。以下のように評価してみます。
\begin{aligned}
\sum_{n=1}^{2023} \frac 2{(n + e^n) } & \leqq \int_0^{2023} \frac{2}{x + e^x} dx \\
& \leqq \sum_{n=1}^{2023} \frac 2{(n-1 + e^{n-1}) }
\end{aligned}必要に応じて x 軸方向の「刻み」を細かくしていけば、定積分の整数値がわかるところまで上下から追い込んでいけるのでは、と思いましたが、よく考えてみると \displaystyle{\frac{2}{n + e^n} } の計算方法がわかりませんorz。
これはもう早々にギブかぁ。でも、もう少し粘ってみます。
不定積分がわかれば積分の整数値がわかるのか
そもそも、不定積分がわかれば積分の整数値がわかるものなのでしょうか。やり方を調べるため、関数 y =\displaystyle \frac{2}{e^x} で実験してみます。
\int_0^{2023} \frac2{e^x} dx =-2 [e^{-x}]_0^{2023} =2(1-e^{-2023}) <2なので、整数部分は1か0だな、とわかりますが、よく考えてみると、すべての x > 0 に対し
\frac 2{x +e^{x} } < \frac 2{e^{x} }なので、
\int_0^{2023} \frac 2{x +e^{x} } dx< \int_0^{2023} \frac 2{e^{x} } dx < 2であり、整数部分が0か1のいずれかであることがソッコーわかりました。
つまりポイントは、被積分関数の上下を不定積分が計算できる関数で挟み撃ちする、ということです。これは行けるのでは!
不定積分 well-known 関数で挟み撃ち
上側の評価は済んでいるので、下側を評価します。
x > 0 の範囲で e^x > x なので、
\begin{aligned}
\int_0^{2023} \frac 2{x +e^{x} } dx & > \int_0^{2023} \frac 2{2e^{x} } dx \\
& = -[e^{-x} ]_0^{2023} =(1-e^{-2023})
\end{aligned}ですが、これだけでは、整数部分が0なのか1なのか判定できません。評価関数のチョイスがイージーすぎたようです。
まじめにやってくだちい(「GANTZ」で主人公が「星人」を倒しそこねた時に、そんなことを言われていた)というわけで、評価関数の選択をもう少し攻めてみます。
直線 y= ax が常に y =e^x の下側にあり(つまり e^x - ax \geqq 0 ) 、かつ、差が一番小さい(つまり一番攻めている)のは、 y= ax が y =e^x に接しているときです(図1)。
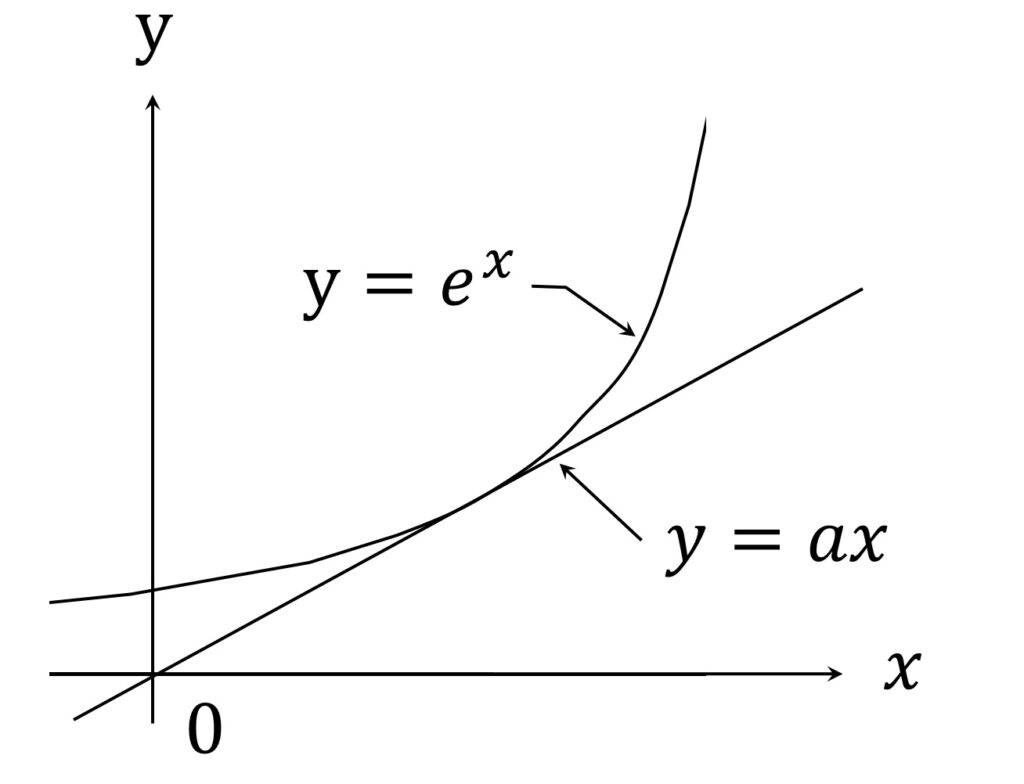
a > 0 の値は具体的に求めることが出来て、それは a = e です( f(x) = e^x- ax の最小値が0になるように a を決めれば良くて、 f(x) の極値が最小値だから、 f'(x)= e^x -a = 0 の解 x = \log a を代入して f(\log a) = 0 より a = e )。
e^x - ex \geqq 0
なので
e^{x-1} \geqq xを得ますが、これを評価に使います。
\begin{aligned}
\int_0^{2023} \frac 2{x +e^{x} } dx & > \int_0^{2023} \frac 2{e^{x-1} +e^{x} } dx \\
& = \int_0^{2023} \frac {2e}{e^{x} (1 +e) } dx \\
& = - \frac{2e}{1+e}[e^{-x} ]_0^{2023} \\
&=\frac{2e}{1+e} (1 -e^{-2023} )
\end{aligned}ですが、
\begin{aligned}
& 2e(1-e^{-2023}) -(1+e) \\
= & e-1- 2 e^{-2022} \\
> & e -1-2\cdot 2^{-2} \\
= & e -\frac3{2} \\
> & 0
\end{aligned}が成り立ちます。ここで、 e > 2 と言う評価を使っています。
よって
\frac{2e}{1+e} (1 -e^{-2023} ) > 1であり、
\begin{aligned}
\int_0^{2023} \frac 2{x +e^{x} } dx & > 1
\end{aligned}です。すなわち、整数部分は1であることが示せました。
天下の東工大なので、 e > 2 を無証明で使用して問題ないと思いますが、上の方で導出した
e^{x-1} \geqq xにおいて、等号が成り立つのは x = 1 のときのみなのと、 x = 2 を代入することによって、導き出すことが出来ます。
解法のポイント

ポイントは何といっても、被積分関数の上下を、積分値を計算できる関数で挟み込むことに気が付くことです。こういう評価が必要な問題はあまり見ないので、これに気づくのはなかなかハードルが高いですが、ここでもう一つのポイントは、本問が積分値の厳密な値を求めているのではなく、整数部分と言う、ある意味ざっくりした評価であることです。
ざっくり評価→ユルっと挟み込み→well-known関数で上下を評価、といった感じで連想を膨らますことが出来れば、正解を得ることが出来ます。何が言えれば問題が解けるのか、常々考えながら問題を解く習慣をつけるようにしましょう。